���嗝�n���w'03�N�O��[1]
a�Cb�Cc�������Ƃ��A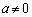 �Ƃ���B2����
�Ƃ���B2����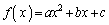 �����̏���(A)�C(B)�����Ƃ���B
�����̏���(A)�C(B)�����Ƃ���B
(A) 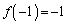 �C
�C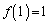 (B)
(B) 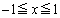 �������ׂĂ�x�ɑ��A
�������ׂĂ�x�ɑ��A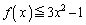
���̂Ƃ��A�ϕ�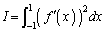 �̂Ƃ肤��l�͈̔͂����߂�B
�̂Ƃ肤��l�͈̔͂����߂�B
�y�L���z��������L���ł��B�����̊F���܂̂��x�������������肽���A��낵�����肢�������܂��B
�y�L���z�L���͂����܂łł��B
���@����ɍς܂���̂ł���A�萔�̕����Ƃ����Z�I���g���Čv�Z���Ă��܂��̂��ǂ��Ǝv���܂��B�ʉ���2�������l���Ă݂܂��B
(A)���A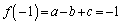 ����@�C
����@�C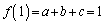 ����A
����A
�@�{�A���A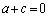 �@��
�@�� 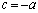
�A�|�@���A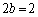 �@��
�@�� 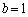
(B)���A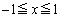 �ɂ����āA
�ɂ����āA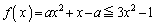 �C
�C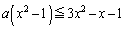 ����B
����B
�B�̌`�̂܂܁A2��2�����̑召�W�������̂͌��������̂�����܂��B
x�ȊO�̕���a���B���̒��Ɉ�����o�Ă��Ȃ��̂ŁA�萔�̕����Ƃ����Z�I���g���܂�(�����@�̕������ւ̉��p(2)���Q��)�B
����a��P�Ƃɐ藣���āA�萔a��x�̊��̑召���ׂ�悤�ɂ���̂ł��B
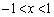 �ɂ�����
�ɂ�����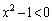 �Ȃ̂ŁA�B�̗��ӂ�
�Ȃ̂ŁA�B�̗��ӂ�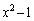 �Ŋ���ƕs�����̌������ς��܂��B
�Ŋ���ƕs�����̌������ς��܂��B
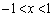 �Ƃ��āA
�Ƃ��āA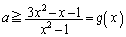 �Ƃ����ƁA
�Ƃ����ƁA
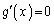 �Ƃ����
�Ƃ����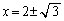
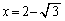 �̂Ƃ��A
�̂Ƃ��A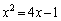 �C
�C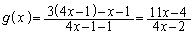 ���A
���A
�����\���(���̑������Q��)�A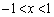 �ɂ����āA
�ɂ����āA
�B�́A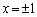 �������Ă݂�ƁAa�̒l�ɂ�����炸�������邱�Ƃ��킩��܂��B
�������Ă݂�ƁAa�̒l�ɂ�����炸�������邱�Ƃ��킩��܂��B
����āA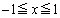 �ɂ����āA
�ɂ����āA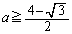 ����C
����C
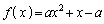 ��������āA
��������āA
�C���A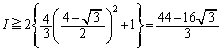 ......[��]
......[��]
�ʉ��@�B��2�����ōl���Ă݂܂��B
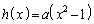 �C
�C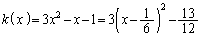
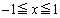 �ɂ����Ă˂�
�ɂ����Ă˂�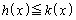 �ƂȂ�������l���܂��B
�ƂȂ�������l���܂��B
�܂��A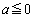 ���Ƃ���ƁA
���Ƃ���ƁA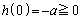 �ł���A
�ł���A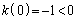 �Ȃ̂ŁA
�Ȃ̂ŁA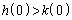 �ƂȂ��Ă��܂��܂��B����āA
�ƂȂ��Ă��܂��܂��B����āA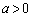 ���K�v�ł��B
���K�v�ł��B
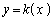 �̃O���t�͉��ɓʂȕ������ł��B
�̃O���t�͉��ɓʂȕ������ł��B
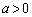 �̂Ƃ��A
�̂Ƃ��A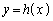 �̃O���t�����ɓʂȕ������ł��Ba�̒l���傫���Ȃ�ƕ������͉s���Ȃ�ƂƂ��ɁA���_��y���W�F
�̃O���t�����ɓʂȕ������ł��Ba�̒l���傫���Ȃ�ƕ������͉s���Ȃ�ƂƂ��ɁA���_��y���W�F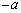 ���ǂ�ǂ����Ȃ�܂��B
���ǂ�ǂ����Ȃ�܂��B
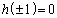 �C
�C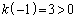 �C
�C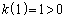 �C�܂��A
�C�܂��A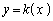 �̃O���t�̎��F
�̃O���t�̎��F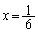 ��
��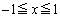 �͈͓̔��ɂ��邱�Ƃ���A
�͈͓̔��ɂ��邱�Ƃ���A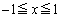 �������ׂĂ�x�ɂ��āA
�������ׂĂ�x�ɂ��āA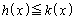 �ƂȂ邽�߂ɂ́Aa�̒l���A
�ƂȂ邽�߂ɂ́Aa�̒l���A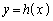 �̃O���t��
�̃O���t��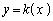 �̃O���t��
�̃O���t��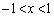 �͈͓̔��ɂ����Đڂ���Ƃ���a�̒l�����傫����悢�A�Ƃ������ƂɂȂ�܂��B
�͈͓̔��ɂ����Đڂ���Ƃ���a�̒l�����傫����悢�A�Ƃ������ƂɂȂ�܂��B
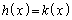 �Ƃ���ƁA
�Ƃ���ƁA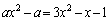
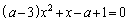 �@����D
�@����D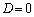 ���A
���A
�� 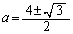
���̂����A�ړ_�̍��W�A�܂�A�d����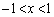 �����̂́A
�����̂́A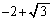 �̕��ŁA���̂Ƃ��A
�̕��ŁA���̂Ƃ��A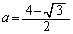
������A(A)�C(B)����a�̏����́A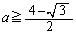 �ƂȂ�܂��B
�ƂȂ�܂��B
�y�L���z��������L���ł��B�����̊F���܂̂��x�������������肽���A��낵�����肢�������܂��B
�y�L���z�L���͂����܂łł��B
�@�@���嗝�n���wTOP�@�@���wTOP�@�@TOP�y�[�W�ɖ߂�
�y�L���z��������L���ł��B�����̊F���܂̂��x�������������肽���A��낵�����肢�������܂��B
�y�L���z�L���͂����܂łł��B
�e���̒��쌠��
�o���w�ɑ����܂��B©2005-2024(�L)����� ��w�y�w�m ���������t���I���n��w�l�b�g�m��w�y�w�m(���ē���������)������́A
�܂��A������܂Ń��[����
�����肭�������B 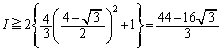 ......[��]
......[��]