���嗝�n���w'03�N�O��[3]
xyz��Ԃɂ����āA����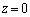 ��̌��_�𒆐S�Ƃ��锼�a2�̉~���ʂƂ��A�_
��̌��_�𒆐S�Ƃ��锼�a2�̉~���ʂƂ��A�_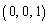 �_�Ƃ���~����A�Ƃ���B
�_�Ƃ���~����A�Ƃ���B
���ɁA����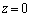 ��̓_
��̓_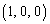 �𒆐S�Ƃ��锼�a1�̉~��H�C����
�𒆐S�Ƃ��锼�a1�̉~��H�C����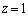 ��̓_
��̓_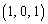 �𒆐S�Ƃ��锼�a1�̉~��K�Ƃ���BH��K��2�̒�ʂƂ���~����B�Ƃ���B�~��A�Ɖ~��B�̋��ʕ�����C�Ƃ���B
�𒆐S�Ƃ��锼�a1�̉~��K�Ƃ���BH��K��2�̒�ʂƂ���~����B�Ƃ���B�~��A�Ɖ~��B�̋��ʕ�����C�Ƃ���B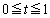 ��������t�ɑ��A����
��������t�ɑ��A����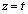 �ɂ��C�̐���̖ʐς�
�ɂ��C�̐���̖ʐς�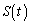 �Ƃ����B
�Ƃ����B
(1) 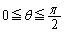 �Ƃ���B
�Ƃ���B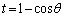 �̂Ƃ��A
�̂Ƃ��A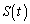 ��θ �ŕ\���B
��θ �ŕ\���B (2) C�̑̐�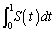 �����߂�B
�����߂�B
�y�L���z��������L���ł��B�����̊F���܂̂��x�������������肽���A��낵�����肢�������܂��B
�y�L���z�L���͂����܂łł��B
���@2�~�̈ʒu�W���ꍇ�킯���Ēf�ʐς��l���܂����A���ǁA�������ɂȂ�܂��B�ϕ��v�Z�͂��Ȃ�ʓ|�ł��B
�Ȃ��A�}�`�ƕ�������O�p���K�������́A�~�̕������A�O�p�����Q�Ƃ��Ă��������B��`�̖ʐςɂ��ẮA��ʊp���A�ϕ��Ɋւ��ẮA�s��ϕ��̌������Q�Ƃ��Ă��������B
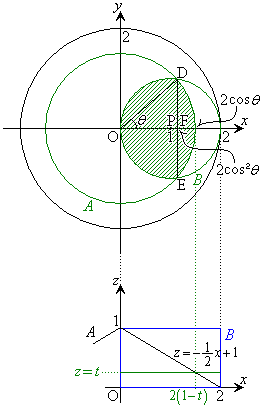 (1)�@����
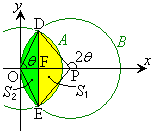
(1)�@����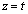 �ɂ��C�̐����z���Ɛ�����xy���ʏ�܂ŕ��s�ړ�������ƉE�}�ΐ����̂悤�ɂȂ�܂�(���̂�^�ォ�猩���}���Ǝv���Ă�������)�B
�ɂ��C�̐����z���Ɛ�����xy���ʏ�܂ŕ��s�ړ�������ƉE�}�ΐ����̂悤�ɂȂ�܂�(���̂�^�ォ�猩���}���Ǝv���Ă�������)�B�~��A��y�����������璭�߂�ƁA�Ő��́A�E���}�̂悤�ɁA����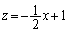 �@����@�@�ɏd�Ȃ��Č����܂��B�@�ɂ����āA
�@����@�@�ɏd�Ȃ��Č����܂��B�@�ɂ����āA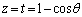 �̂Ƃ��A
�̂Ƃ��A 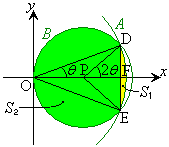 a)
a) 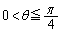 �̂Ƃ��A2�~�̈ʒu�W�͉E�}�̂悤�ɂȂ�܂��B
�̂Ƃ��A2�~�̈ʒu�W�͉E�}�̂悤�ɂȂ�܂��B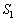 �́A��`ODE����O�p�`ODE������������(�E�}�ʼn��F���h��ꂽ����)�̖ʐςŁA
�́A��`ODE����O�p�`ODE������������(�E�}�ʼn��F���h��ꂽ����)�̖ʐςŁA�܂��A���S�p�͉~���p��2�{�Ȃ̂ŁA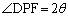
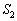 �́A�~�B�����h��`PDE����O�p�`PDE�������������h������������(�E�}�ʼn��ΐF�ɓh��ꂽ����)�̖ʐςŁA
�́A�~�B�����h��`PDE����O�p�`PDE�������������h������������(�E�}�ʼn��ΐF�ɓh��ꂽ����)�̖ʐςŁA �� 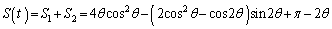
 b)
b) 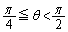 �̂Ƃ��A2�~�̈ʒu�W�͉E�}�̂悤�ɂȂ�܂��B
�̂Ƃ��A2�~�̈ʒu�W�͉E�}�̂悤�ɂȂ�܂��B
 ��a)�̏ꍇ�Ɠ����ł��B
��a)�̏ꍇ�Ɠ����ł��B
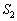 �͐�`PDE����O�p�`PDE�������������̖ʐςŁA
�͐�`PDE����O�p�`PDE�������������̖ʐςŁA�����a)�̏ꍇ�Ɠ����ł��B
����āA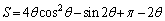 ......[��]
......[��]
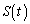 ��θ �̎��ŗ^�����Ă���̂ŁA�u���ϕ����s���At�̐ϕ���θ �̐ϕ��ɒ����܂��B
��θ �̎��ŗ^�����Ă���̂ŁA�u���ϕ����s���At�̐ϕ���θ �̐ϕ��ɒ����܂��B
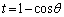 ��������āA
��������āA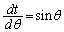
�� 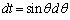
t�F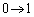 �̂Ƃ��Aθ �F
�̂Ƃ��Aθ �F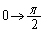
����āA�� 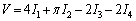
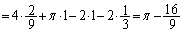 .......[��]
.......[��]
�y�L���z��������L���ł��B�����̊F���܂̂��x�������������肽���A��낵�����肢�������܂��B
�y�L���z�L���͂����܂łł��B
�@�@���嗝�n���wTOP�@�@���wTOP�@�@TOP�y�[�W�ɖ߂�
�y�L���z��������L���ł��B�����̊F���܂̂��x�������������肽���A��낵�����肢�������܂��B
�y�L���z�L���͂����܂łł��B
�e���̒��쌠��
�o���w�ɑ����܂��B©2005-2024(�L)����� ��w�y�w�m ���������t���I���n��w�l�b�g�m��w�y�w�m(���ē���������)������́A
�܂��A������܂Ń��[����
�����肭�������B