���嗝�n���w'03�N�O��[4]
2��������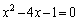 ��2�̎������̂����傫�����̂�α�C���������̂�β �Ƃ���B
��2�̎������̂����傫�����̂�α�C���������̂�β �Ƃ���B
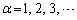 �ɑ��A
�ɑ��A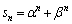 �Ƃ����B
�Ƃ����B(1) 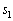 �C
�C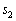 �C
�C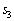 �����߂�B�܂��A
�����߂�B�܂��A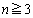 �ɑ��A
�ɑ��A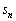 ��
��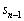 ��
��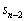 �ŕ\���B
�ŕ\���B (2) 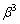 �ȉ��̍ő�̐��������߂�B
�ȉ��̍ő�̐��������߂�B (3) 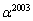 �ȉ��̍ő�̐�����1�̈ʂ̐������߂�B
�ȉ��̍ő�̐�����1�̈ʂ̐������߂�B
�y�L���z��������L���ł��B�����̊F���܂̂��x�������������肽���A��낵�����肢�������܂��B
�y�L���z�L���͂����܂łł��B
���@������3���ԑQ�����̗Z�����ł��B
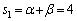 ......[��]
......[��]
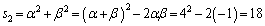 ......[��]
......[��]
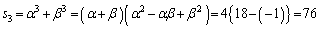 ......[��]
......[��]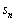 �C
�C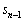 �C
�C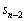 ��3���̊Ԃ̊W�������߂�̂ł����A3���ԑQ�����F
��3���̊Ԃ̊W�������߂�̂ł����A3���ԑQ�����F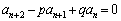 ����A ���������̈�ʍ������߂�Ƃ��ɏo�Ă���u�����������v�ƌĂ��2���������F
����A ���������̈�ʍ������߂�Ƃ��ɏo�Ă���u�����������v�ƌĂ��2���������F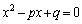 ���������Ƃ��v���o���܂��B����2���������̉���α�Cβ �Ƃ���ƁA�A���A
���������Ƃ��v���o���܂��B����2���������̉���α�Cβ �Ƃ���ƁA�A���A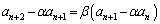 (����β�����䐔��)�C�܂��́A
(����β�����䐔��)�C�܂��́A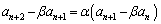 (����α�̓��䐔��)�ƕό`���邱�Ƃ��ł��āA�ŏI�I�ɁA��ʍ�
(����α�̓��䐔��)�ƕό`���邱�Ƃ��ł��āA�ŏI�I�ɁA��ʍ�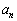 ���A
���A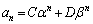 ����B �̌`�ɕ\�����Ƃ��ł��܂��B
����B �̌`�ɕ\�����Ƃ��ł��܂��B
�Ƃ������Ƃ́A��ʍ���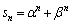 �̌`�ɕ\���Ă��āAα�Cβ ��2���������F
�̌`�ɕ\���Ă��āAα�Cβ ��2���������F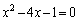 �̉��Ȃ�A����
�̉��Ȃ�A����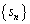 ���]��3���ԑQ�����́A
���]��3���ԑQ�����́A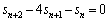 �̂͂��ł��B�����ł́A
�̂͂��ł��B�����ł́A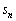 �C
�C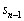 �C
�C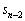 �̊W�����Ă���̂ŁA
�̊W�����Ă���̂ŁA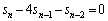 �ƂȂ邱�ƂׂĂ݂܂��B
�ƂȂ邱�ƂׂĂ݂܂��B
α�Cβ �́A2���������F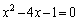 �̉��ł�����A
�̉��ł�����A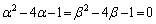 �ł��B
�ł��B
�]���āA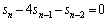 ......[��]
......[��]
(2) 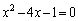 �������ƁA
�������ƁA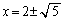
����āA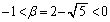
�� 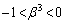
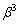 �ȉ��̍ő�̐����́A
�ȉ��̍ő�̐����́A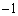 ......[��]
......[��]
(3) (1)�œ���ꂽ3���ԑQ������p����ƁA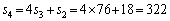 �C
�C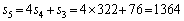
�ƂȂ�̂ŁA����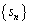 ��1�̈ʂ́A4�C8�C6�C2�C4�C8�C6�C2�C4�C...... �Ƃ������4�����z���Ă䂭���Ƃ��\���ł��܂��B
��1�̈ʂ́A4�C8�C6�C2�C4�C8�C6�C2�C4�C...... �Ƃ������4�����z���Ă䂭���Ƃ��\���ł��܂��B
����𐔊w�I�A�[�@�ŏؖ����邱�Ƃɂ��܂��B
�܂��A���������Ă����܂��B4�����ꂽ���̊Ԃ̊W�ׂ�悢�̂ŁA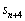 ��
��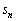 �̊Ԃ̊W�ׂ܂��B(1)�œ���ꂽ�Q�������J��Ԃ��Ďg�����Ƃɂ��A
�̊Ԃ̊W�ׂ܂��B(1)�œ���ꂽ�Q�������J��Ԃ��Ďg�����Ƃɂ��A ����āA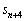 ��1�̈ʂ̐����́A
��1�̈ʂ̐����́A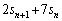 ��1�̈ʂ̐����Ɉ�v���܂��B���(��)����F0�ȏ�̐���m�ɂ��āA
��1�̈ʂ̐����Ɉ�v���܂��B���(��)����F0�ȏ�̐���m�ɂ��āA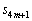 �C
�C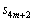 �C
�C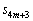 �C
�C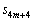 ��1�̈ʂ̐������A�e�X�A4�C8�C6�C2�ł��邱�Ƃ����w�I�A�[�@��p���ďؖ����܂��B(�T)
��1�̈ʂ̐������A�e�X�A4�C8�C6�C2�ł��邱�Ƃ����w�I�A�[�@��p���ďؖ����܂��B(�T) 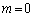 �̂Ƃ��A
�̂Ƃ��A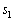 �C
�C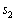 �C
�C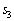 �C
�C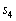 ��1�̈ʂ̐����́A4�C8�C6�C2�Ȃ̂ŁA����͐��藧���܂��B(�U)
��1�̈ʂ̐����́A4�C8�C6�C2�Ȃ̂ŁA����͐��藧���܂��B(�U) 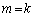 �̂Ƃ��A���肪���藧�Ƃ��āA
�̂Ƃ��A���肪���藧�Ƃ��āA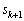 �C
�C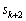 �C
�C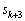 �C
�C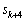 ��1�̈ʂ̐������A�e�X�A4�C8�C6�C2���Ɖ��肵�܂��B(��)�ɂ��A
��1�̈ʂ̐������A�e�X�A4�C8�C6�C2���Ɖ��肵�܂��B(��)�ɂ��A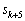 ��1�̈ʂ̐����́A
��1�̈ʂ̐����́A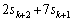 ��1�̈ʂ̐����Ɉ�v���܂��B
��1�̈ʂ̐����Ɉ�v���܂��B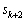 �C
�C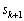 ��10�̈ʂ̐�����1�̈ʂɂ͊�^���Ȃ��̂ŁA1�̈ʂ̐���8�C4�������Ă䂯�悢�̂ł��B
��10�̈ʂ̐�����1�̈ʂɂ͊�^���Ȃ��̂ŁA1�̈ʂ̐���8�C4�������Ă䂯�悢�̂ł��B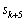 ��1�̈ʂ̐����́A
��1�̈ʂ̐����́A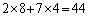 ��1�̈ʂ�4�ɂȂ�܂��B����B
��1�̈ʂ�4�ɂȂ�܂��B����B
���l�ɂ��āA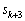 �C
�C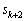 ��1�̈ʂ̐���6�C8����A
��1�̈ʂ̐���6�C8����A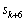 ��1�̈ʂ̐����́A
��1�̈ʂ̐����́A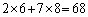 ��1�̈ʂ�8�ɂȂ�܂��B
��1�̈ʂ�8�ɂȂ�܂��B
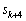 �C
�C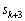 ��1�̈ʂ̐���2�C6����A
��1�̈ʂ̐���2�C6����A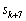 ��1�̈ʂ̐����́A
��1�̈ʂ̐����́A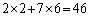 ��1�̈ʂ�6�ɂȂ�܂��B
��1�̈ʂ�6�ɂȂ�܂��B
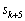 �C
�C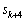 ��1�̈ʂ̐���4�C2����A
��1�̈ʂ̐���4�C2����A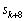 ��1�̈ʂ̐����́A�B���A
��1�̈ʂ̐����́A�B���A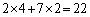 ��1�̈ʂ�2�ɂȂ�܂��B
��1�̈ʂ�2�ɂȂ�܂��B
����āA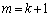 �ɂ����Ă��A���肪�������܂��B(�T)�C(�U)���A���肪�ؖ�����܂����B
�ɂ����Ă��A���肪�������܂��B(�T)�C(�U)���A���肪�ؖ�����܂����B
�Ƃ���ŁA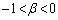 ���A
���A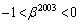 �ł��B
�ł��B
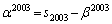 �ł����A��L�̖�����A
�ł����A��L�̖�����A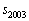 ��1�̈ʂ̐����́A
��1�̈ʂ̐����́A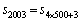 ���A6�ł��B
���A6�ł��B
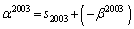 ��1�̈ʂ̂̐����́A
��1�̈ʂ̂̐����́A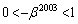 ���A
���A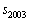 �Ɠ������A6 ......[��]
�Ɠ������A6 ......[��]
�y�L���z��������L���ł��B�����̊F���܂̂��x�������������肽���A��낵�����肢�������܂��B
�y�L���z�L���͂����܂łł��B
�@�@���嗝�n���wTOP�@�@���wTOP�@�@TOP�y�[�W�ɖ߂�
�y�L���z��������L���ł��B�����̊F���܂̂��x�������������肽���A��낵�����肢�������܂��B
�y�L���z�L���͂����܂łł��B
�e���̒��쌠��
�o���w�ɑ����܂��B©2005-2024(�L)����� ��w�y�w�m ���������t���I���n��w�l�b�g�m��w�y�w�m(���ē���������)������́A
�܂��A������܂Ń��[����
�����肭�������B