���嗝�n���w'04�N�O��[6]
�Жʂ𔒐F�ɁA�����Жʂ����F�ɓh���������`�̔�3������B����3���̔����̏�ɉ��ɕ��ׁA���̑�����J��Ԃ��s���B
���������U��A�o���ڂ�1�C2�ł�����[�̔𗠕Ԃ��A3�C4�ł���܂̔𗠕Ԃ��A5�C6�ł���ΉE�[�̔𗠕Ԃ��B
���Ƃ��A�ŏ��A�̕\�̐F�̕��ѕ����u�������v�ł������Ƃ��A1��ڂ̑���ŏo����������̖ڂ�1�ł���A�F�̕��ѕ��́u�������v�ƂȂ�B�����2��ڂ̑�����s���ďo����������̖ڂ�5�ł���A�F�̕��ѕ��́u�������v�ƂȂ�B
(1) �u�������v����n�߂āA3��̑���̌��ʁA�F�̕��ѕ����u�������v�ƂȂ�m�������߂�B
(2) �u�������v����n�߂āAn��̑���̌��ʁA�F�̕��ѕ����u�������v�܂��́u�������v�ƂȂ�m�������߂�B
���ӁF���������1����6�܂ł̖ڂ����m���ŏo����̂Ƃ���B
�y�L���z��������L���ł��B�����̊F���܂̂��x�������������肽���A��낵�����肢�������܂��B
�y�L���z�L���͂����܂łł��B
���@(1)�ŁA���ۂ̐��ڂ̃J���N���ׂ�ƂƂ��ɁA�m���̐���̏��������߁A(2)�ŁA�Q����������Ċm�������߂�Ƃ����I�[�\�h�b�N�X�Ȋm���Q�����̖��ł��B�Q�������ϑ��I�ŁA�J���N�������j��̂�������Ɠ�q���܂����A�悭����^�C�v�̖��ł��B
(1) 1�C2���o�鎖�ہA3�C4���o�鎖�ہA5�C6���o�鎖�ۂ́A�ǂ���m��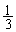 �ŋN����܂��B
�ŋN����܂��B �]���āA���[�̔A�܂̔A�E�[�̔����ւ��Ă��m���͕ς��܂����B
������������U���āA�u�������v�ɂȂ�m���A�u�������v�ɂȂ�m���A�u�������v�ɂȂ�m���͓����ł��B
�܂��A�u�������v�ɂȂ�m���A�u�������v�ɂȂ�m���A�u�������v�ɂȂ�m���͓����ł��B
�u�������v����1�������U��ƁA�u�������v���u�������v���u�������v�̂����ꂩ�ɂȂ�܂��B
�u�������v���炳���1�������U��ƁA�u�������v���u�������v���u�������v�ɂȂ�܂��B
���̎��_�ŁA���̖�����0���܂���2���ł��B
�u�������v�A�u�������v���炳���1�������U���Ă��A���̖�����0����2���ł��B
������A�����������U��ƁA���̖�����0����2���ɂȂ肻���ł��B1����U��Ȃ��Ƃ����܂߂āA���������������U�����Ƃ��ɁA���̖�����0���A�܂��́A2�����Ƃ��܂��B
����0���̂Ƃ��ɁA�������ɕς��ƁA���̖�����1���ɂȂ�܂��B
����2���̂Ƃ��ɁA�������ɕς��ƁA���̖�����1���ɁA�������ɕς��ƁA���̖�����3���ɂȂ�܂��B
�]���āA������������U��ƁA���̖�����1���A�܂���3���ł��B
���̌�A1�������U��ƁA
���̖�����1���̂Ƃ��ɁA�������ɕς��ƁA���̖�����0���ɁA�������ɕς��ƁA���̖�����2���ɂȂ�܂��B
���̖�����3���̂Ƃ��ɁA�������ɕς��ƁA���̖�����2���ɂȂ�܂��B
�]���āA���������������U��ƁA���̖�����0���A�܂���2���ł��B3�������U���āA�u�������v�ɂȂ�̂́A1�C2��1��A3�C4��1��A5�C6��1��o��ꍇ�ł��B(1�C2)�C(3�C4)�C(5�C6)�̕��ו����A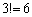 �ʂ肠��̂ŁA
�ʂ肠��̂ŁA
���̊m���́A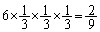 �ł��B ����@3�������U���āA�u�������v�ɂȂ鎖�ۂ̗]���ۂ́A�u�������v���u�������v���u�������v�ɂȂ鎖���ł�(�a���ہE�ώ��ہE�]�������Q��)�B
�ł��B ����@3�������U���āA�u�������v�ɂȂ鎖�ۂ̗]���ۂ́A�u�������v���u�������v���u�������v�ɂȂ鎖���ł�(�a���ہE�ώ��ہE�]�������Q��)�B
����3�̎��ۂ͂ǂ�����m���ŋN����̂ŁA3�������U���āA�u�������v�ƂȂ�m���́A 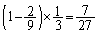 ......[��]
......[��]
(2) (1)�ŏ������悤�ɁA������������U��ƁA���̖�����1���A�܂���3���ɂȂ�܂��B
����āA�A���A���������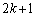 ��U���āu�������v�ƂȂ�m���́A
��U���āu�������v�ƂȂ�m���́A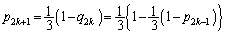
�� 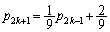 ����B�@(2���ԑQ�������Q��)
����B�@(2���ԑQ�������Q��)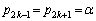 �Ƃ����ƁA
�Ƃ����ƁA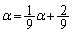 ����C
����C
�� 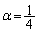 �B�|�C���A
�B�|�C���A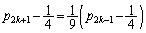
����āA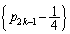 �́A�����F
�́A�����F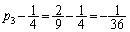 �C����F
�C����F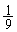 �̓��䐔��ł����āA
�̓��䐔��ł����āA �� 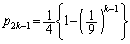 ����D
����D
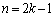 �̂Ƃ��A
�̂Ƃ��A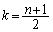
������D�ɑ������ƁA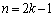 ��(���)���������U���āA�u�������v�ƂȂ�m���́A
��(���)���������U���āA�u�������v�ƂȂ�m���́A �u�������v�ƂȂ�m���́A�u�������v�ƂȂ鎖�ۂ̗]���ۂ̊m����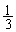 ������A
������A ���̑���ŁA�u�������v�ƂȂ邱�Ƃ͂���܂���B
�A�C�D���A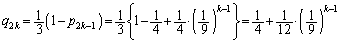 ����E
����E
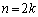 �̂Ƃ��A
�̂Ƃ��A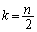
������E�ɑ������ƁA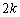 ��(������)���������U���āA�u�������v�ƂȂ�m���́A
��(������)���������U���āA�u�������v�ƂȂ�m���́A ������̑���ŁA�u�������v�ƂȂ邱�Ƃ͂���܂���B
�ȏ���Ak�����R���Ƃ��āA�u�������v�܂��́u�������v�ƂȂ�m���́A
�E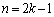 �̂Ƃ��A
�̂Ƃ��A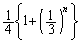 ......[��]
......[��] �E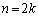 �̂Ƃ��A
�̂Ƃ��A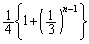 ......[��]
......[��]
�y�L���z��������L���ł��B�����̊F���܂̂��x�������������肽���A��낵�����肢�������܂��B
�y�L���z�L���͂����܂łł��B
�@�@���嗝�n���wTOP�@�@���wTOP�@�@TOP�y�[�W�ɖ߂�
�y�L���z��������L���ł��B�����̊F���܂̂��x�������������肽���A��낵�����肢�������܂��B
�y�L���z�L���͂����܂łł��B
�e���̒��쌠��
�o���w�ɑ����܂��B©2005-2024(�L)����� ��w�y�w�m ���������t���I���n��w�l�b�g�m��w�y�w�m(���ē���������)������́A
�܂��A������܂Ń��[����
�����肭�������B