東大理系数学'05年前期[3]
とする。ただし、eは自然対数の底である。
(1) 
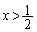ならば
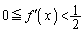であることを示せ。 (2) 
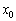を正の数とするとき、数列
(
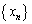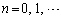)を、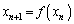
によって定める。
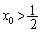であれば、 であることを示せ。
【広告】ここから広告です。ご覧の皆さまのご支援ご理解を賜りたく、よろしくお願いいたします。
【広告】広告はここまでです。
解答 この問題は京大'84[6]をはじめとして、あちこちの大学で出題されてきている問題です。東大でも、毎年1題か2題、入試頻出技巧を使う問題が出題されています。
2次の導関数は、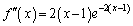
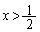における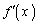
の増減表は、増減表より、
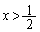において、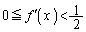
また、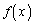
は単調増加関数。
(2) 原問題で特に聞かれているわけではないのですが、定型問題なので、ふつうこうやる、という筋道でやっていきます。
という方程式を考えます。(1)で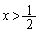
という条件をつけているので、ここでも、
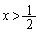の範囲の解を考えます。ここで、 という関数を考えます。
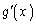の増減表は、増減表より、
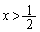において、
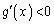，従って、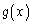
は単調減少関数です。より、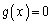
，即ち、
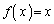は、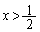
において、ただ1つの解
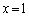を持ちます。
・まず、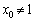
の場合を考えます。 
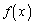は単調増加で
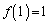なので、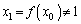
以下、同様にして、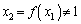
，
，･･････
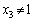となり、全ての自然数nについて、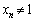
です。
また、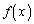
は単調増加関数だから、
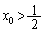より、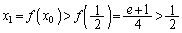
，
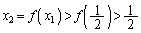，･･････となり、全ての自然数nについて、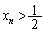
です。
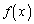は、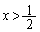
において微分可能な関数なので、平均値の定理より、
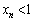の場合には
，
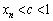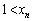の場合には、
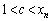として、 となるcが存在します。どちらの場合においても、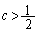
なので、(1)の結果より、 この不等式で項の番号を1ずつ小さくしてゆくと、
これらを使って、
∴ 
∴ 
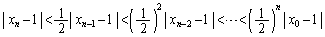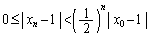
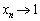
より、全ての0以上の整数nについて、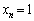
以上より、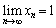
......[答]
【広告】ここから広告です。ご覧の皆さまのご支援ご理解を賜りたく、よろしくお願いいたします。
【広告】広告はここまでです。
東大理系数学TOP 数学TOP TOPページに戻る
【広告】ここから広告です。ご覧の皆さまのご支援ご理解を賜りたく、よろしくお願いいたします。
【広告】広告はここまでです。
各問題の著作権は
出題大学に属します。©2005-2024(有)りるらる 苦学楽学塾 随時入会受付中！理系大学受験ネット塾苦学楽学塾(ご案内はこちら)ご入会は、
まず、こちらまでメールを
お送りください。 
，
，･･･，
の場合には、
，
，･･････
)
)
とすると、右辺
