���嗝�n���w'11�N�O��[6]
(1) x�Cy�������Ƃ��A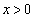 �Ƃ���Bt��ϐ��Ƃ���2����
�Ƃ���Bt��ϐ��Ƃ���2����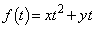 ��
��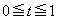 �ɂ�����ő�l�ƍŏ��l�̍������߂�B
�ɂ�����ő�l�ƍŏ��l�̍������߂�B (2) ���̏��������_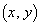 �S�̂���Ȃ���W���ʓ��̗̈��S�Ƃ���B
�S�̂���Ȃ���W���ʓ��̗̈��S�Ƃ���B 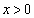 ���A����z��
���A����z��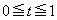 �͈̔͂̑S�Ă̎���t�ɑ���
�͈̔͂̑S�Ă̎���t�ɑ��������悤�Ȃ��̂����݂���B
S�̊T�`��}������B
(3) ���̏��������_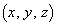 �S�̂���Ȃ���W��ԓ��̗̈��V�Ƃ���B
�S�̂���Ȃ���W��ԓ��̗̈��V�Ƃ���B 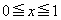 ���A
���A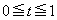 �͈̔͂̑S�Ă̎���t�ɑ��āA
�͈̔͂̑S�Ă̎���t�ɑ��āA�����藧�B
V�̑̐ς����߂�B
�y�L���z��������L���ł��B�����̊F���܂̂��x�������������肽���A��낵�����肢�������܂��B
�y�L���z�L���͂����܂łł��B
���@(1)�͂悭����2�����̍ő�E�ŏ����ł��B(2)�C(3)�̑�ӂ����Â炢�̂ł����A��蕶�Ɂu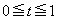 �͈̔͂̑S�Ă̎���t�ɑ��āv�Ə�����Ă���̂ŁA
�͈̔͂̑S�Ă̎���t�ɑ��āv�Ə�����Ă���̂ŁA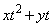 ��(1)�ŋ��߂��ő�l
��(1)�ŋ��߂��ő�l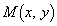 �C�ŏ��l
�C�ŏ��l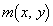 �Œu�������ĕs�������l���܂��B
�Œu�������ĕs�������l���܂��B
(2)��(3)�ʼn����Ⴄ�̂��낤�Ǝv�������m��܂���B�b��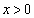 ����
����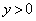 �Ɍ���A(3)�̏�������
�Ɍ���A(3)�̏�������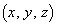 �́A
�́A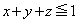 �����A
�����A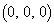 �C
�C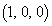 �C
�C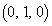 �C
�C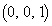 ��4���_�Ƃ���l�ʑ̂̓����ɂȂ�܂����A(2)�ł́A�l�ʑ̂����݂���
��4���_�Ƃ���l�ʑ̂̓����ɂȂ�܂����A(2)�ł́A�l�ʑ̂����݂���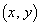 �͈̔́A�܂�A
�͈̔́A�܂�A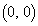 �C
�C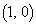 �C
�C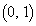 ��3���_�Ƃ���O�p�`�̓���(���̎O�p�`�̏㑤��(3)�̎l�ʑ̂����݂���)�A���Ă��܂��B�܂�A(3)�ł͗��̂����߂Ă���̂ɑ��A(2)�ł͗��̂����݂���
��3���_�Ƃ���O�p�`�̓���(���̎O�p�`�̏㑤��(3)�̎l�ʑ̂����݂���)�A���Ă��܂��B�܂�A(3)�ł͗��̂����߂Ă���̂ɑ��A(2)�ł͗��̂����݂���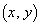 �͈̔͂����߂Ă��܂��B
�͈̔͂����߂Ă��܂��B
(2)�C(3)�́A�ȉ��łׂ͍��������Ă��܂����A���E���ƂȂ钼���A�Ȑ������G�ɗ��ݍ����A�{�Ԃł͐��m�ȋL�q�ɂ������Ɩҗ�ɖʓ|�ŁA���Ԃ����X����̂Œ��ӂ��Ă��������B
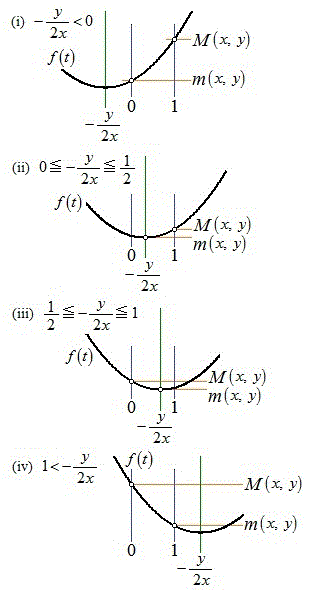 (1) x�Cy�ɑ��āA
(1) x�Cy�ɑ��āA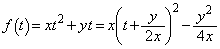 ��
��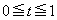 �ɂ�����ő�l��
�ɂ�����ő�l��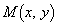 �C�ŏ��l��
�C�ŏ��l��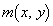 �Ƃ��܂�(2�����̍ő�ŏ����Q��)�B
�Ƃ��܂�(2�����̍ő�ŏ����Q��)�B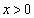 �̂Ƃ��A
�̂Ƃ��A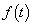 �̃O���t�͉��ɓʂȕ������ŁA�E�}���A
�̃O���t�͉��ɓʂȕ������ŁA�E�}���A(i) 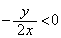 �C�܂�A
�C�܂�A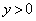 �̂Ƃ��A
�̂Ƃ��A 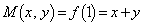 �C
�C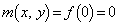
(ii) 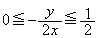 �C�܂�A
�C�܂�A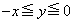 �̂Ƃ��A
�̂Ƃ��A 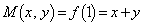 �C
�C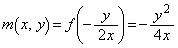
(iii) 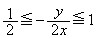 �C�܂�A
�C�܂�A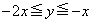 �̂Ƃ��A
�̂Ƃ��A 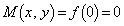 �C
�C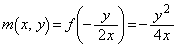
(iv) 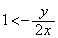 �C�܂�A
�C�܂�A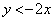 �̂Ƃ��A
�̂Ƃ��A 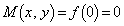 �C
�C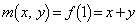
�ȏ���A�ő�l�ƍŏ��l�̍��́A
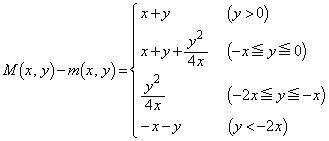 ......[��]
......[��]
(2) 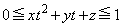 ��
�� 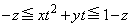
��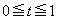 �͈̔͂̑S�Ă̎���t�ɑ��Đ��藧�悤��z�����݂��邽�߂ɁA
�͈̔͂̑S�Ă̎���t�ɑ��Đ��藧�悤��z�����݂��邽�߂ɁA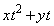 �̍ő�l�C�ŏ��l��
�̍ő�l�C�ŏ��l��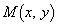 �C
�C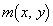 �ł��邱�Ƃ��A
�ł��邱�Ƃ��A 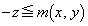 �C
�C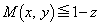
�� 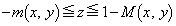 �@����@
�@����@
�@����z�����݂��邽�߂ɁA
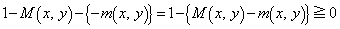
�� 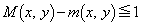 �@����A
�@����A
�ȉ��A�ꍇ�������ćA�ׂ܂��B (i) 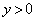 �̂Ƃ��A(1)�ƇA���A
�̂Ƃ��A(1)�ƇA���A �� 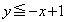
(ii) 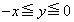 �̂Ƃ��A(1)�ƇA���A
�̂Ƃ��A(1)�ƇA���A ������Đ�������ƁA
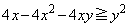 �C
�C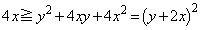
�� 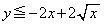 ���E���́A
���E���́A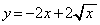 �C
�C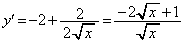 �C�����\�͈ȉ��̒ʂ�(���̑������Q��)�B
�C�����\�͈ȉ��̒ʂ�(���̑������Q��)�B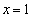 �ɂ������ڐ���
�ɂ������ڐ���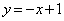 �ł����(i)�̋��E���ł��B
�ł����(i)�̋��E���ł��B
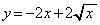 ��
��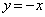 ��A������ƁA
��A������ƁA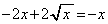 �C
�C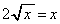
�� 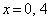 �C
�C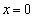 �̂Ƃ�
�̂Ƃ�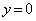 �C
�C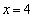 �̂Ƃ�
�̂Ƃ�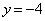
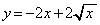 ��
��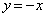 �̌�_��
�̌�_��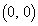 �C
�C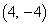 �ł��B
�ł��B (iii) 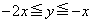 �̂Ƃ��A(1)�ƇA���A
�̂Ƃ��A(1)�ƇA���A 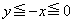 ���A
���A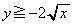
���E����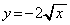
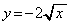 ��
��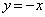 ��A������ƁA
��A������ƁA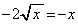
�� 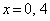 �C
�C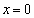 �̂Ƃ�
�̂Ƃ�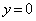 �C
�C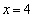 �̂Ƃ�
�̂Ƃ�
 ��
�� �̌�_��
�̌�_�� �C
�C
 ��
�� ��A������ƁA
��A������ƁA
�� 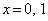 �C
�C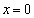 �̂Ƃ�
�̂Ƃ�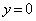 �C
�C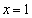 �̂Ƃ�
�̂Ƃ�
 ��
�� �̌�_��
�̌�_�� �C
�C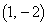
(iv) 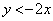 �̂Ƃ��A(1)�ƇA���A
�̂Ƃ��A(1)�ƇA���A 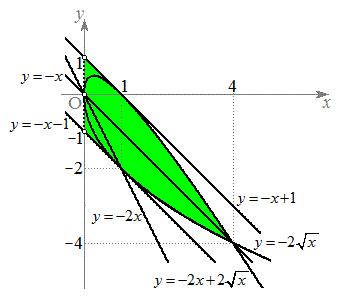 >>(i)�`(iv)���A�̈�S�́A
>>(i)�`(iv)���A�̈�S�́A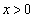 ����
���� 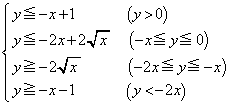 �}������ƉE�}���ΐF���F��(���E���́Ay����݂̂������B�܂�A��������܂݁A�_����A���}�����܂܂Ȃ�)�B
�}������ƉE�}���ΐF���F��(���E���́Ay����݂̂������B�܂�A��������܂݁A�_����A���}�����܂܂Ȃ�)�B
(3) ���x�͖�蕶�̕s��������z�����݂���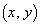 �͈̔͂����߂�̂ł͂Ȃ��A(2)��
�͈̔͂����߂�̂ł͂Ȃ��A(2)�� 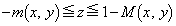 �@����@
�@����@����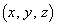 �͈̔͂����߂邱�ƂɂȂ�܂��BV�̑̐ς����߂�̂ŁAz���ɐ����ȕ��ʂŐ����Ƃ��̒f�ʂ��l���邽�߂ɁA�ȉ��ł�z���Œ肵�čl���܂��B
�͈̔͂����߂邱�ƂɂȂ�܂��BV�̑̐ς����߂�̂ŁAz���ɐ����ȕ��ʂŐ����Ƃ��̒f�ʂ��l���邽�߂ɁA�ȉ��ł�z���Œ肵�čl���܂��B (i) 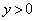 �̂Ƃ��A(1)(i)�Ƈ@���A
�̂Ƃ��A(1)(i)�Ƈ@���A (ii) 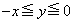 �̂Ƃ��A(1)(ii)�Ƈ@���A
�̂Ƃ��A(1)(ii)�Ƈ@���A ���E���́A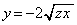 ��
��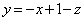 �ł��B
�ł��B
������A������ƁA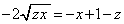
�A���A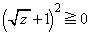 �C
�C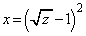 �̂Ƃ�
�̂Ƃ�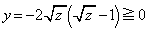 �ł�(
�ł�(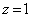 �ȊO�ł�
�ȊO�ł�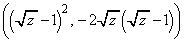 �͗̈�O�̓_�ł�)�B
�͗̈�O�̓_�ł�)�B
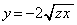 ��
��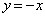 ��A������ƁA
��A������ƁA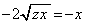
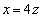 �̂Ƃ��A
�̂Ƃ��A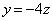
��_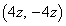 �́A
�́A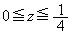 �̂Ƃ�
�̂Ƃ�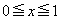 �͈͓̔��̓_�C
�͈͓̔��̓_�C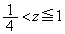 �̂Ƃ��͈͊O�̓_�ł��B(iii)���܂߂āA���̒��D�Ō������܂��B
�̂Ƃ��͈͊O�̓_�ł��B(iii)���܂߂āA���̒��D�Ō������܂��B
�܂��A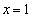 �̂Ƃ��A�Ȑ�
�̂Ƃ��A�Ȑ�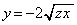 �ɂ����Ă�
�ɂ����Ă�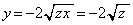 �C����
�C����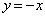 �ɂ����Ă�
�ɂ����Ă�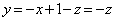 �C�܂��A����
�C�܂��A����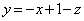 ��x���Ƃ̌�_
��x���Ƃ̌�_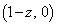 ��
��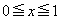 �͈͓̔��ɂ���܂��B
�͈͓̔��ɂ���܂��B(iii) 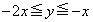 �̂Ƃ��A(1)(iii)�Ƈ@���A
�̂Ƃ��A(1)(iii)�Ƈ@���A 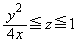 �@(
�@(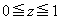 �ł�)
�ł�)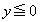 ���A
���A���E���́A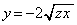 �ł��B
�ł��B
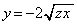 ��
��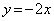 ��A������ƁA
��A������ƁA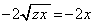
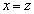 �̂Ƃ��A
�̂Ƃ��A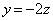
�܂��A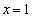 �̂Ƃ��A����
�̂Ƃ��A����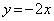 �ɂ����Ă�
�ɂ����Ă�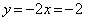 �C��_
�C��_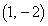 ��
��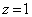 �ȊO�ł͗̈�O�̓_�ł��B
�ȊO�ł͗̈�O�̓_�ł��B���D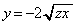 ��
��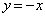 �Ƃ̌�_
�Ƃ̌�_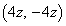 �́A
�́A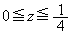 �̂Ƃ��̈�
�̂Ƃ��̈�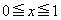 ���̓_�ł����A
���̓_�ł����A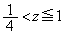 �̂Ƃ��̈�
�̂Ƃ��̈�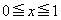 �̒��ɓ���܂���(�ȉ��̐}�́A���̏ꍇ��z�肵�ĕ`����Ă��܂�)�B
�̒��ɓ���܂���(�ȉ��̐}�́A���̏ꍇ��z�肵�ĕ`����Ă��܂�)�B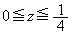 �̂Ƃ��ɂ�(iii)�Œ���
�̂Ƃ��ɂ�(iii)�Œ���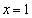 �͋��E���ɏo�Ă��܂��A
�͋��E���ɏo�Ă��܂��A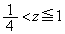 �̂Ƃ��ɂ�(ii)��
�̂Ƃ��ɂ�(ii)��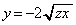 �͋��E���ɏo�Ă��܂���B������ɂ���A(ii)�C(iii)���킹�āAx���Cy���C����
�͋��E���ɏo�Ă��܂���B������ɂ���A(ii)�C(iii)���킹�āAx���Cy���C����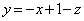 �C����
�C����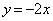 �C
�C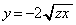 �C����
�C����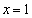 �Ɉ͂܂ꂽ�}�`�ɂȂ�܂��B
�Ɉ͂܂ꂽ�}�`�ɂȂ�܂��B 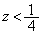 �C
�C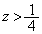 ��
��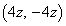 �ƒ���
�ƒ���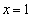 �̈ʒu�W���ς���Ă��܂��̂ŁA���́A�{��ł́A
�̈ʒu�W���ς���Ă��܂��̂ŁA���́A�{��ł́A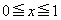 �Ǝw�肳��Ă��邱�Ƃ�����Az���Œ肷�����x���Œ肷��������N�ł��B
�Ǝw�肳��Ă��邱�Ƃ�����Az���Œ肷�����x���Œ肷��������N�ł��B(iv) 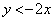 �̂Ƃ��A
�̂Ƃ��A ���E���́A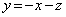 �ł��B
�ł��B
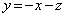 ��
��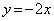 ��A������ƁA
��A������ƁA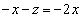
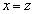 �C
�C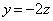
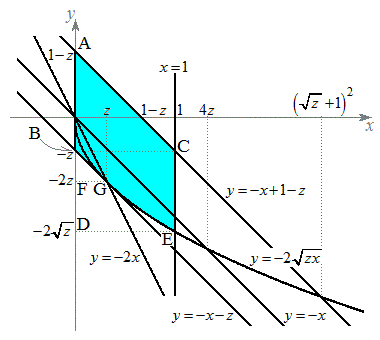 �ȏ���A�̈�V��z���ɐ����ȕ��ʂŐ����Ƃ��̒f�ʂ��Az���ɐ�����zx���ʏ�ɕ��s�ړ����Ăł���̈�͉E�}���F���F���B
�ȏ���A�̈�V��z���ɐ����ȕ��ʂŐ����Ƃ��̒f�ʂ��Az���ɐ�����zx���ʏ�ɕ��s�ړ����Ăł���̈�͉E�}���F���F���B
���̖ʐ�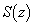 �́A��ABC�̖ʐςƒ����`BCED�̖ʐς̘a���灢BFG�̖ʐς������A����ɁA�Ȑ�
�́A��ABC�̖ʐςƒ����`BCED�̖ʐς̘a���灢BFG�̖ʐς������A����ɁA�Ȑ�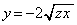 (
(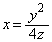 )��y���C����FG�F
)��y���C����FG�F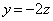 �C����DE�F
�C����DE�F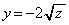 �ň͂܂�镔���̖ʐς����������̂Ƃ���(��ϕ��Ɩʐ����Q��)�A
�ň͂܂�镔���̖ʐς����������̂Ƃ���(��ϕ��Ɩʐ����Q��)�A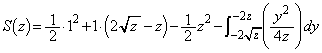 �@(
�@(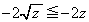 �ɒ���)
�ɒ���)V�����݂���̂�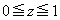 �ŁAV�̑̐ς́A
�ŁAV�̑̐ς́A 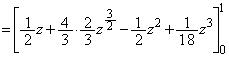
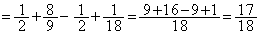 ......[��]
......[��]
�y�L���z��������L���ł��B�����̊F���܂̂��x�������������肽���A��낵�����肢�������܂��B
�y�L���z�L���͂����܂łł��B
�@�@���嗝�n���wTOP�@�@���wTOP�@�@TOP�y�[�W�ɖ߂�
�y�L���z��������L���ł��B�����̊F���܂̂��x�������������肽���A��낵�����肢�������܂��B
�y�L���z�L���͂����܂łł��B
�e���̒��쌠��
�o���w�ɑ����܂��B©2005-2024(�L)����� ��w�y�w�m ���������t���I���n��w�l�b�g�m��w�y�w�m(���ē���������)������́A
�܂��A������܂Ń��[����
�����肭�������B 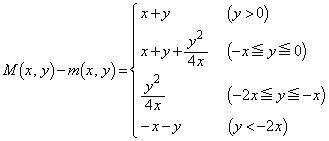 ......[��]
......[��]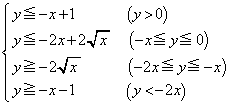
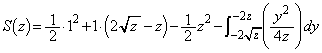 �@(
�@(