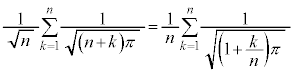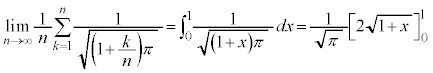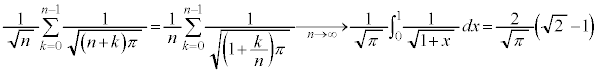���嗝�n���w'23�N�O��[1]
(1) ���̐���k�ɑ��A
�Ƃ����B���̕s���������藧���Ƃ������B
(2) ���̐���n�ɑ��A
�Ƃ����B�Ɍ�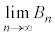 �����߂�B
�����߂�B
�y�L���z��������L���ł��B�����̊F���܂̂��x�������������肽���A��낵�����肢�������܂��B
�y�L���z�L���͂����܂łł��B
���@�܂��͌����炵�A�Ƃ������ł��B
(1) 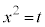 �Ƃ�����(�u���ϕ����Q��)�A
�Ƃ�����(�u���ϕ����Q��)�A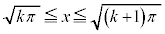 �ɂ����Ă�
�ɂ����Ă�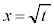 �C
�C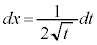 �Cx�F
�Cx�F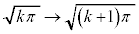 �̂Ƃ��At�F
�̂Ƃ��At�F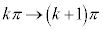
�Ek�������̂Ƃ��A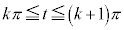 �ɂ����āA
�ɂ����āA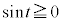 (�O�p�����Q��)
(�O�p�����Q��) 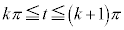 �ɂ����āA
�ɂ����āA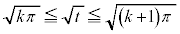 �C
�C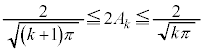 �@����@
�@����@�Ek����̂Ƃ��A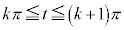 �ɂ����āA
�ɂ����āA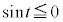 �C�܂�A
�C�܂�A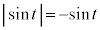
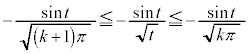 (
(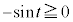 )���A
)���A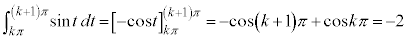 ���A��͂�@�ƂȂ�܂��B
���A��͂�@�ƂȂ�܂��B
����āAk�̋�������ɂ��Ă��A
(2) 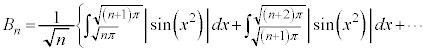
(1)��p���āA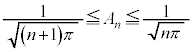
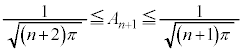 �@�@������
�@�@������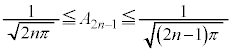
�ӁX������ƁA
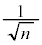 �������āA
�������āA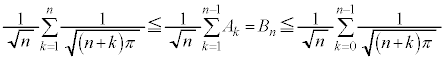 �@����A
�@����A���ӂɂ��āA
�A�̉E�ӂɂ��Ă��A
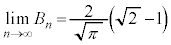 ......[��]
......[��]
�y�L���z��������L���ł��B�����̊F���܂̂��x�������������肽���A��낵�����肢�������܂��B
�y�L���z�L���͂����܂łł��B
�@�@���嗝�n���wTOP�@�@���wTOP�@�@TOP�y�[�W�ɖ߂�
�y�L���z��������L���ł��B�����̊F���܂̂��x�������������肽���A��낵�����肢�������܂��B
�y�L���z�L���͂����܂łł��B
�e���̒��쌠��
�o���w�ɑ����܂��B©2005-2024(�L)����� ��w�y�w�m ���������t���I���n��w�l�b�g�m��w�y�w�m(���ē���������)������́A
�܂��A������܂Ń��[����
�����肭�������B 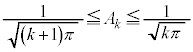
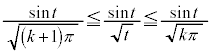
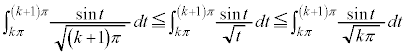
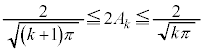 �@����@
�@����@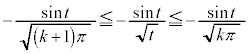 (
(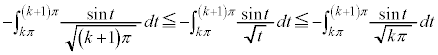
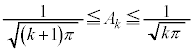
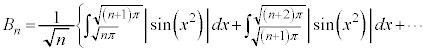
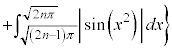
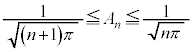
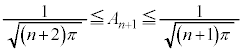
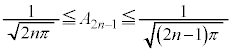
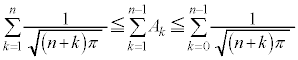
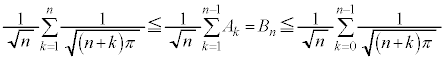 �@����A
�@����A