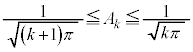東京大学理系2023年前期数学入試問題
【広告】ここから広告です。ご覧の皆さまのご支援ご理解を賜りたく、よろしくお願いいたします。
【広告】広告はここまでです。
[1](1) 正の整数kに対し、
とおく。次の不等式が成り立つことを示せ。
(2) 正の整数nに対し、
とおく。極限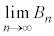 を求めよ。
を求めよ。 [解答へ]
[2] 黒玉3個、赤玉4個、白玉5個が入っている袋から玉を1個ずつ取り出し、取り出した玉を順に横一列に12個すべて並べる。ただし、袋から個々の玉が取り出される確率は等しいものとする。
(1) どの赤玉も隣り合わない確率pを求めよ。
(2) どの赤玉も隣り合わないとき、どの黒玉も隣り合わない条件付き確率qを求めよ。
[解答へ]
[3] aを実数とし、座標平面上の点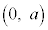 を中心とする半径1の円の周をCとする。
を中心とする半径1の円の周をCとする。
(1) Cが、不等式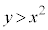 の表す領域に含まれるようなaの範囲を求めよ。
の表す領域に含まれるようなaの範囲を求めよ。 (2) aは(1)で求めた範囲にあるとする。Cのうち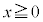 かつ
かつ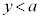 を満たす部分をSとする。S上の点Pに対し、点PでのCの接線が放物線
を満たす部分をSとする。S上の点Pに対し、点PでのCの接線が放物線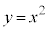 によって切り取られてできる線分の長さを
によって切り取られてできる線分の長さを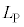 とする。
とする。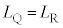 となるS上の相異なる2点Q,Rが存在するようなaの範囲を求めよ。
となるS上の相異なる2点Q,Rが存在するようなaの範囲を求めよ。 [解答へ]
[4] 座標空間内の4点O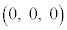 ,A
,A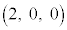 ,B
,B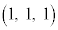 ,C
,C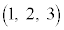 を考える。
を考える。
(2) 点Pから直線ABに垂線を下ろし、その垂線と直線ABの交点をHとする。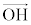 を
を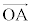 と
と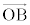 を用いて表せ。
を用いて表せ。 (3) 点Qを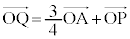 により定め、Qを中心とする半径rの球面Sを考える。Sが三角形OHBと共有点を持つようなrの範囲を求めよ。ただし、三角形OHBは3点O,H,Bを含む平面内にあり、周とその内部からなるものとする。
により定め、Qを中心とする半径rの球面Sを考える。Sが三角形OHBと共有点を持つようなrの範囲を求めよ。ただし、三角形OHBは3点O,H,Bを含む平面内にあり、周とその内部からなるものとする。 [解答へ]
[5] 整式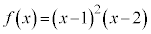 を考える。
を考える。
(1) 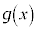 を実数を係数とする整式とし、
を実数を係数とする整式とし、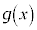 を
を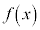 で割った余りを
で割った余りを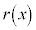 とおく。
とおく。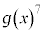 を
を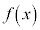 で割った余りと
で割った余りと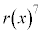 を
を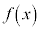 で割った余りが等しいことを示せ。
で割った余りが等しいことを示せ。 (2) a,bを実数とし、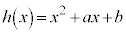 とおく。
とおく。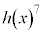 を
を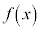 で割った余りを
で割った余りを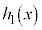 とおき、
とおき、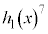 を
を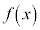 で割った余りを
で割った余りを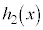 とおく。
とおく。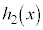 が
が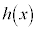 に等しくなるようなa,bの組をすべて求めよ。
に等しくなるようなa,bの組をすべて求めよ。 [解答へ]
[6] Oを原点とする座標空間において、不等式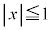 ,
,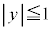 ,
,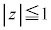 の表す立方体を考える。その立方体の表面のうち、
の表す立方体を考える。その立方体の表面のうち、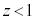 を満たす部分をSとする。
を満たす部分をSとする。
以下、座標空間内の2点A,Bが一致するとき、線分ABは点Aを表すものとし、その長さを0と定める。
(1) 座標空間内の点Pが次の条件(i),(ii)をともに満たすとき、点Pが動きうる範囲Vの体積を求めよ。
(i) 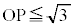
(ii) 線分OPとSは、共有点を持たないか、点Pのみを共有点にもつ。
(2) 座標空間内の点Nと点Pが次の条件(iii),(iv),(v)をすべて満たすとき、点Pが動きうる範囲Wの体積を求めよ。必要ならば、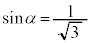 を満たす実数α (
を満たす実数α (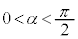 )を用いてよい。
)を用いてよい。 (iii) 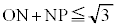
(iv) 線分ONとSは共有点を持たない。
(v) 線分NPとSは、共有点を持たないか、点Pのみを共有点に持つ。
[解答へ]
【広告】ここから広告です。ご覧の皆さまのご支援ご理解を賜りたく、よろしくお願いいたします。
【広告】広告はここまでです。
東大理系数学TOP 数学TOP TOPページに戻る
【広告】ここから広告です。ご覧の皆さまのご支援ご理解を賜りたく、よろしくお願いいたします。
【広告】広告はここまでです。
各問題の著作権は
出題大学に属します。©2005-2024(有)りるらる 苦学楽学塾 随時入会受付中!理系大学受験ネット塾苦学楽学塾(ご案内はこちら)ご入会は、
まず、こちらまでメールを
お送りください。