���嗝�n���w'23�N�O��[4]
���W��ԓ���4�_O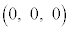 �CA
�CA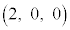 �CB
�CB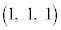 �CC
�CC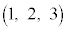 ���l����B
���l����B
(1) 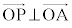 �C
�C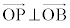 �C
�C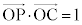 �����_P�̍��W�����߂�B
�����_P�̍��W�����߂�B (2) �_P���璼��AB�ɐ��������낵�A���̐����ƒ���AB�̌�_��H�Ƃ���B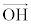 ��
��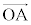 ��
��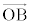 ��p���ĕ\���B
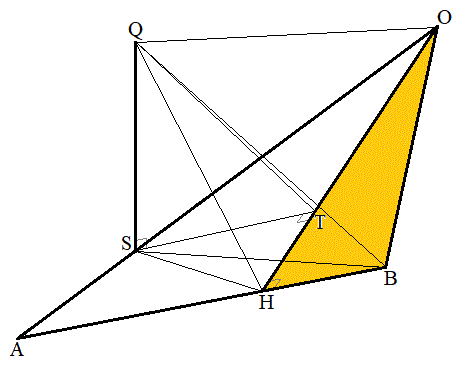
��p���ĕ\���B (3) �_Q��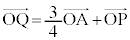 �ɂ���߁AQ�𒆐S�Ƃ��锼�ar�̋���S���l����BS���O�p�`OHB�Ƌ��L�_�����悤��r�͈̔͂����߂�B�������A�O�p�`OHB��3�_O�CH�CB���܂ޕ��ʓ��ɂ���A���Ƃ��̓�������Ȃ���̂Ƃ���B
�ɂ���߁AQ�𒆐S�Ƃ��锼�ar�̋���S���l����BS���O�p�`OHB�Ƌ��L�_�����悤��r�͈̔͂����߂�B�������A�O�p�`OHB��3�_O�CH�CB���܂ޕ��ʓ��ɂ���A���Ƃ��̓�������Ȃ���̂Ƃ���B
�y�L���z��������L���ł��B�����̊F���܂̂��x�������������肽���A��낵�����肢�������܂��B
�y�L���z�L���͂����܂łł��B
���@(3)�́A(1)�ʼn�������Ă����̂��A�Ƃ������ƂɋC�Â��Ȃ��Ƃ���グ�ɂȂ�܂��B
(1) 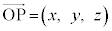 �Ƃ����܂��B
�Ƃ����܂��B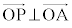 ���(�������Q��)�A
���(�������Q��)�A 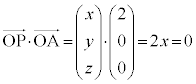 �@��
�@�� 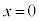
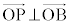 ���A
���A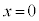 ���A
���A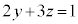
�@���A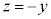 �C����������āA
�C����������āA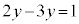 �@��
�@�� 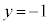 �C
�C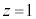
����āAP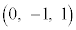 ......[��]
......[��]
(2) H�͒���AB��̓_�Ȃ̂�p�������Ƃ��āA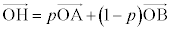 �@����A�@�Ƃ����܂�(�����������Q��)�B
�@����A�@�Ƃ����܂�(�����������Q��)�B (1)�̌��ʂ�p���āA
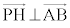 ���A
���A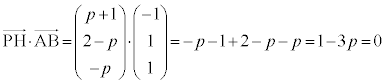 �@��
�@�� 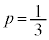
�A���A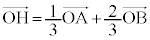 ......[��]�@����B
......[��]�@����B
(3) ����S���O�p�`OHB�Ƌ��L�_�����悤�Ȕ��ar�͈̔͂Ƃ����̂́A�O�p�`OHB��̓_R�Ƌ���S�̒��SQ�Ƃ̋���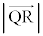 �͈̔͂̂��Ƃł��B�܂��A�f���ɍl���Ă݂܂��B
�͈̔͂̂��Ƃł��B�܂��A�f���ɍl���Ă݂܂��B 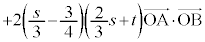 �@(��
�@(�� 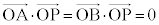 )
)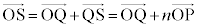 �@����D
�@����DS�͕���OAB��̓_�ŁA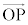 �ƕ���OAB�͐����Ȃ̂ŁA
�ƕ���OAB�͐����Ȃ̂ŁA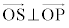 �C����ćD���A
�C����ćD���A 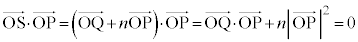 �@����E
�@����E(1)�̌��ʂ��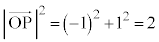 �C
�C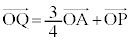 ���A
���A 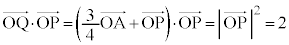 �@(��
�@(�� 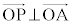 )
)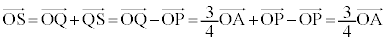 �@����F
�@����F�����S�́AOA��3�F1�ɓ�������_�ł��B���̂Ƃ��A
�ł��B�܂��AQ�ƕ���OAB��̓_�Ƃ̋������ŏ��ɂȂ镽��OAB��̓_��S�Ȃ̂ŁA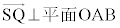 �ł���A����OAB���S�ȊO�̓_R�ɑ��A
�ł���A����OAB���S�ȊO�̓_R�ɑ��A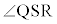 �͒��p�ł��B�O�����̒藝���A
�͒��p�ł��B�O�����̒藝���A ������A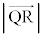 ���ő�A�ŏ��̂Ƃ��A
���ő�A�ŏ��̂Ƃ��A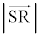 ���ő�A�ŏ��ł��B
���ő�A�ŏ��ł��B
 �B���AH��AB��2�F1�ɓ�������_(�x�N�g���̓����E�O�����Q��)�ł���A�E�}���A
�B���AH��AB��2�F1�ɓ�������_(�x�N�g���̓����E�O�����Q��)�ł���A�E�}���A ���ŏ��ɂ���O�p�`OHB���̓_�́AS�������OH�ɐ���ST�����낷�Ƃ���T�ł��B
���ŏ��ɂ���O�p�`OHB���̓_�́AS�������OH�ɐ���ST�����낷�Ƃ���T�ł��B �Ȃ̂ŁAST // AB�ł���AOT�FTH = OS�FSA = 3�F1
�Ȃ̂ŁAST // AB�ł���AOT�FTH = OS�FSA = 3�F1 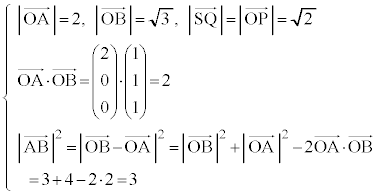 �@����G
�@����G���A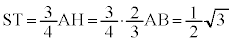
����āA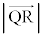 �̍ŏ��l�́A
�̍ŏ��l�́A 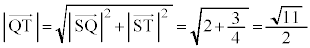 �@����H
�@����H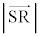 ���ő�ɂ���O�p�`OHB���̓_�́A���_O�CH�CB�̂ǂꂩ�ł��B�G��p���āA
���ő�ɂ���O�p�`OHB���̓_�́A���_O�CH�CB�̂ǂꂩ�ł��B�G��p���āA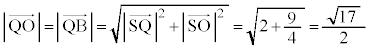 �@����I
�@����I�H�C�I���A����S���O�p�`OHB�Ƌ��L�_�����悤�Ȕ��ar�͈̔͂́A
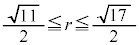 ......[��]
......[��]
�y�L���z��������L���ł��B�����̊F���܂̂��x�������������肽���A��낵�����肢�������܂��B
�y�L���z�L���͂����܂łł��B
�@�@���嗝�n���wTOP�@�@���wTOP�@�@TOP�y�[�W�ɖ߂�
�y�L���z��������L���ł��B�����̊F���܂̂��x�������������肽���A��낵�����肢�������܂��B
�y�L���z�L���͂����܂łł��B
�e���̒��쌠��
�o���w�ɑ����܂��B©2005-2024(�L)����� ��w�y�w�m ���������t���I���n��w�l�b�g�m��w�y�w�m(���ē���������)������́A
�܂��A������܂Ń��[����
�����肭�������B 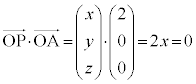 �@��
�@�� 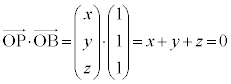
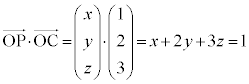
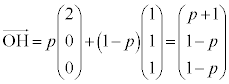
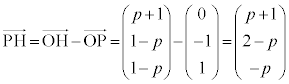
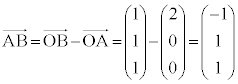
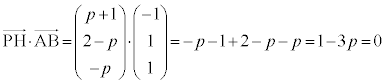 �@��
�@�� 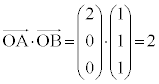 ��������ƁA
��������ƁA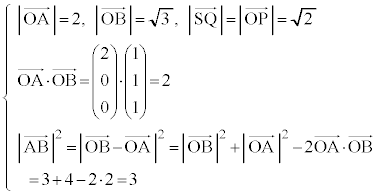 �@����G
�@����G