���嗝�n���w'23�N�O��[6]
O�����_�Ƃ�����W��Ԃɂ����āA�s����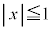 �C
�C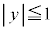 �C
�C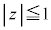 �̕\�������̂��l����B���̗����̂̕\�ʂ̂����A
�̕\�������̂��l����B���̗����̂̕\�ʂ̂����A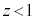 ����������S�Ƃ���B
����������S�Ƃ���B
�ȉ��A���W��ԓ���2�_A�CB����v����Ƃ��A����AB�͓_A��\�����̂Ƃ��A���̒�����0�ƒ�߂�B
(1) ���W��ԓ��̓_P�����̏���(i)�C(ii)���Ƃ��ɖ������Ƃ��A�_P����������͈�V�̑̐ς����߂�B
(i) 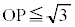
(ii) ����OP��S�́A���L�_�������Ȃ����A�_P�݂̂����L�_�ɂ��B
(2) ���W��ԓ��̓_N�Ɠ_P�����̏���(iii)�C(iv)�C(v)�����ׂĖ������Ƃ��A�_P����������͈�W�̑̐ς����߂�B�K�v�Ȃ�A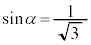 ��������α (
��������α (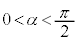 )��p���Ă悢�B
)��p���Ă悢�B (iii) 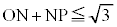
(iv) ����ON��S�͋��L�_�������Ȃ��B
(v) ����NP��S�́A���L�_�������Ȃ����A�_P�݂̂����L�_�Ɏ��B
�y�L���z��������L���ł��B�����̊F���܂̂��x�������������肽���A��낵�����肢�������܂��B
�y�L���z�L���͂����܂łł��B
���@�v�Z�͂����łȂ��A��ԓI���o���K�v�ȓ��ł��B�Ȃ��A�{��́A���̂�z���ɐ����ȖʂŐ��Ēf�ʐς�ϕ����悤�Ƃ���ƁA�s���l�܂�܂��B
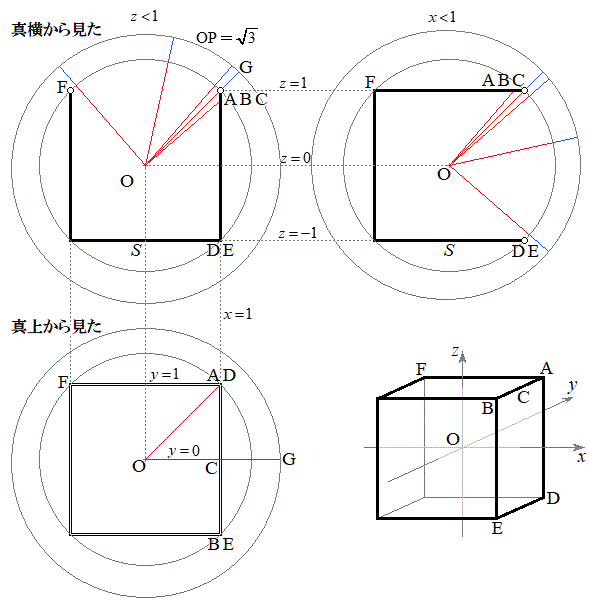 (1) ��蕶�̗����̂�1��2�̗����̂ł��B�܂��A���_O�𒆐S�Ƃ��锼�a
(1) ��蕶�̗����̂�1��2�̗����̂ł��B�܂��A���_O�𒆐S�Ƃ��锼�a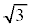 �̋��ʂ�Σ�Ƃ��܂��B�����̂̕\�ʂ̂����A
�̋��ʂ�Σ�Ƃ��܂��B�����̂̕\�ʂ̂����A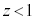 ����������S�Ƃ���̂ŁA
����������S�Ƃ���̂ŁA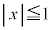 �C
�C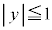 �C
�C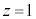 ���������ł��鐳���`R�̓����y�ю��̒��̂ǂ����̓_
���������ł��鐳���`R�̓����y�ю��̒��̂ǂ����̓_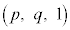 (
(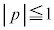 �C
�C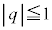 )�����OP���ʉ߂���Ƃ��ɂ́A����OP��S�͋��L�_�������܂���B���̂Ƃ��A(i)��
)�����OP���ʉ߂���Ƃ��ɂ́A����OP��S�͋��L�_�������܂���B���̂Ƃ��A(i)��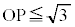 �̏������AP�͋���Σ�y�т��̓����ɂ���܂��B
�̏������AP�͋���Σ�y�т��̓����ɂ���܂��B�_A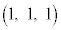 �CB
�CB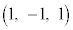 �Ƃ���ƁA����AB�͗����̂�1�ӂł���A�����`R��1�ӂł��B����OP������AB��̓_(S��̓_�ł͂Ȃ�)�Ƌ��L�_�����Ƃ��A����OP��S�Ƌ��L�_�������Ȃ��̂ŁAP�͋���Σ�y�т��̓����ɂ���A
�Ƃ���ƁA����AB�͗����̂�1�ӂł���A�����`R��1�ӂł��B����OP������AB��̓_(S��̓_�ł͂Ȃ�)�Ƌ��L�_�����Ƃ��A����OP��S�Ƌ��L�_�������Ȃ��̂ŁAP�͋���Σ�y�т��̓����ɂ���A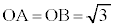 ���A����OP���ʉ߂���͈͂́A����OA�COB�ɋ��܂ꂽ���a
���A����OP���ʉ߂���͈͂́A����OA�COB�ɋ��܂ꂽ���a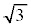 �̐�`(�ȉ���`OAB�Ƃ��܂�)�ɂȂ�܂��B
�̐�`(�ȉ���`OAB�Ƃ��܂�)�ɂȂ�܂��B
����OP��R�̑���3�ӂƋ��L�_�����ꍇ�����l�ł��B
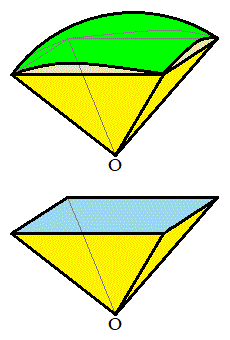 �������āA����OP�������`R�̎���܂��͓����̓_�����L�_�����Ƃ��AP�̓����͈͂́A����Σ��4�̐�`�Ɉ͂܂ꂽ�}�`
�������āA����OP�������`R�̎���܂��͓����̓_�����L�_�����Ƃ��AP�̓����͈͂́A����Σ��4�̐�`�Ɉ͂܂ꂽ�}�`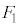 (�E�})�ƂȂ邱�Ƃ�������܂��BS�������̕\�ʂ̂����A
(�E�})�ƂȂ邱�Ƃ�������܂��BS�������̕\�ʂ̂����A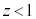 �ł͂Ȃ��Ⴆ�A
�ł͂Ȃ��Ⴆ�A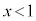 ���������Ƃ��ė^������ꍇ�ɂ��A
���������Ƃ��ė^������ꍇ�ɂ��A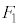 �Ɠ��l�ɁAP�̓����͈͂́AO�𒆐S�Ƃ��锼�a
�Ɠ��l�ɁAP�̓����͈͂́AO�𒆐S�Ƃ��锼�a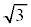 �̋��ʂƁA4�̐�`�Ɉ͂܂ꂽ�}�`�ł����āA�����
�̋��ʂƁA4�̐�`�Ɉ͂܂ꂽ�}�`�ł����āA�����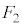 �Ƃ���ƁA
�Ƃ���ƁA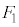 ��
��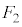 �͑S������̐}�`�ł��B�܂��A�E��}�̂悤�ɁAO��ʂ����AB�ォ��͂��ɂ��ꂽ�_��ʉ߂��钼�����l����킩��ʂ�A
�͑S������̐}�`�ł��B�܂��A�E��}�̂悤�ɁAO��ʂ����AB�ォ��͂��ɂ��ꂽ�_��ʉ߂��钼�����l����킩��ʂ�A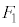 ��
��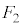 �́A�Ƃ��ɐ�`OAB���܂ݐ�`OAB�Őڂ��Ă��܂��B
�́A�Ƃ��ɐ�`OAB���܂ݐ�`OAB�Őڂ��Ă��܂��B
�����̂ɂ́A6�̖ʂ�����܂����A�����`R (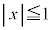 �C
�C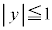 �C
�C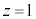 )�ȊO�̂ǂ̖ʂɂ��Ă����l�ŁA�S������̐}�`
)�ȊO�̂ǂ̖ʂɂ��Ă����l�ŁA�S������̐}�`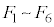 ���ł��܂��B�����������͂ǂ�����a
���ł��܂��B�����������͂ǂ�����a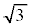 �̐�`�Őڂ��Ă���A�����̐�`�œ\�荇�킹��悤��
�̐�`�Őڂ��Ă���A�����̐�`�œ\�荇�킹��悤��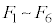 �����킹��ƁA����Σ�y�т��̓����ɂȂ�܂��B�]���āA
�����킹��ƁA����Σ�y�т��̓����ɂȂ�܂��B�]���āA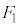 �̑̐ς͋��̑̐ς�
�̑̐ς͋��̑̐ς�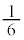 �ŁA
�ŁA 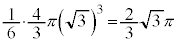
�}�`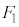 �́A�E�}�̂悤�ɁA�����̂̓����ƂȂ�l�p���Ɨ����̂̊O���ɂ��镔���Ƃɕ����邱�Ƃ��ł��܂��B�����̂̓����ƂȂ�l�p���́A��ʐ�
�́A�E�}�̂悤�ɁA�����̂̓����ƂȂ�l�p���Ɨ����̂̊O���ɂ��镔���Ƃɕ����邱�Ƃ��ł��܂��B�����̂̓����ƂȂ�l�p���́A��ʐ�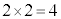 �C����1�ŁA�̐ς�
�C����1�ŁA�̐ς�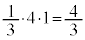 �ł����A���̎l�p����6���킹��Ƒ̐�8�̗����̂ɂȂ�܂��B
�ł����A���̎l�p����6���킹��Ƒ̐�8�̗����̂ɂȂ�܂��B
�}�`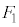 �̂����A�����̂̊O���ɂȂ镔���̑̐�
�̂����A�����̂̊O���ɂȂ镔���̑̐�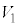 �́A
�́A P�������`R��̓_�ɂȂ邩�A����OP�������`R�Ƌ��L�_�������Ȃ��ꍇ�AP�̑��ݔ͈͂͗����̂̓����ɂȂ�A���̑̐ς�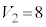 �ł��B����OP�������`R�Ƌ��L�_�����ꍇ��P�̑��ݔ͈͂̑̐ς�
�ł��B����OP�������`R�Ƌ��L�_�����ꍇ��P�̑��ݔ͈͂̑̐ς�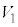 �ł��B
�ł��B
����āA�_P����������͈�V�̑̐ς́A 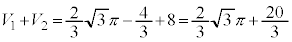 ......[��]
......[��]
(2) (iii)�C(iv)�C(v)�̏����́A(1)��OP�������I�������̂ɑ��āAOP��N�̂Ƃ���Ő܂�Ȃ����Ă��Ă��悢�A�Ƃ������Ƃ��Ӗ����Ă��܂��B����(iii)�C(iv)���AN�̓�������͈͂�(1)�͈̔�V����S����������͈͂ł��B����ɁA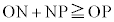 (�O�p�`�̏������Q��)�Ȃ̂ŁA
(�O�p�`�̏������Q��)�Ȃ̂ŁA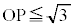 �ł���AO�CN�CP���꒼����ɕ��ԏꍇ���l����A(1)�͈̔�V���̓_�͏���(iii)(iv)(v)�����܂��B�܂��A
�ł���AO�CN�CP���꒼����ɕ��ԏꍇ���l����A(1)�͈̔�V���̓_�͏���(iii)(iv)(v)�����܂��B�܂��A 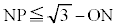 �@����@
�@����@���AP��N�𒆐S�Ƃ��锼�a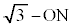 �̋��������Ƃ��ł��܂��B�����P�́A(1)�͈̔�V�S�̂����łȂ��͈�V�̊O�����������Ƃ��ł��܂��B
�̋��������Ƃ��ł��܂��B�����P�́A(1)�͈̔�V�S�̂����łȂ��͈�V�̊O�����������Ƃ��ł��܂��B
�����ŁA�_P����������͈�W��V����ǂꂭ�炢�L���邩���l���邱�Ƃɂ��܂��BN���͈�V���̗����̓�(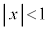 �C
�C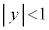 �C
�C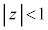 )�Ɉʒu����ꍇ�ɂ́A(v)�̏��������_P�́A�����̓��ɂ��邩�A����Σ�y�т��̓����ɂ���̂ŁA�͈�V����O���ɂ͏o�čs���܂���BP���͈�V����O���ɏo��Ƃ��ANP��傫���Ƃ邽�߂ɂ́AN��(1)�̐}�`
)�Ɉʒu����ꍇ�ɂ́A(v)�̏��������_P�́A�����̓��ɂ��邩�A����Σ�y�т��̓����ɂ���̂ŁA�͈�V����O���ɂ͏o�čs���܂���BP���͈�V����O���ɏo��Ƃ��ANP��傫���Ƃ邽�߂ɂ́AN��(1)�̐}�`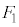 �̋��E�ʂ�
�̋��E�ʂ�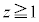 �ƂȂ镔��((1)�E��̒��F�}�̔����F�̕���)�̂ǂ����Ɉʒu���Ȃ���Ȃ�܂���BN��(1)�E��}�̗����̂̒��_A
�ƂȂ镔��((1)�E��̒��F�}�̔����F�̕���)�̂ǂ����Ɉʒu���Ȃ���Ȃ�܂���BN��(1)�E��}�̗����̂̒��_A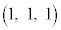 �Ɉʒu����Ƃ��A
�Ɉʒu����Ƃ��A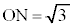 �Ȃ̂ŁA�@���A
�Ȃ̂ŁA�@���A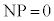 �ƂȂ�P��A�ɗ��܂��BN��(1)�E��}�ŕ�AB�̒��_C
�ƂȂ�P��A�ɗ��܂��BN��(1)�E��}�ŕ�AB�̒��_C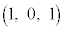 �Ɉʒu����Ƃ��A
�Ɉʒu����Ƃ��A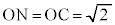 �Ȃ̂ŁA�@���A
�Ȃ̂ŁA�@���A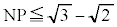 �ƂȂ�AP��N (C�ɂ���)�𒆐S�Ƃ��锼�a
�ƂȂ�AP��N (C�ɂ���)�𒆐S�Ƃ��锼�a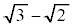 �̋�
�̋�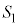 �����܂��B(1)�E��}�Œ���OC�ƁA����Σ�Ƃ̌�_(2��_�̂���C�ɋ߂���)��G�Ƃ��āAN������CG��Ɉʒu����Ƃ��AP��N�𒆐S�Ƃ��锼�a
�����܂��B(1)�E��}�Œ���OC�ƁA����Σ�Ƃ̌�_(2��_�̂���C�ɋ߂���)��G�Ƃ��āAN������CG��Ɉʒu����Ƃ��AP��N�𒆐S�Ƃ��锼�a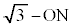 �̋������܂����A���̋��́A���
�̋������܂����A���̋��́A���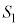 ��G�Őڂ���悤�ɓ��ڂ��Ă���AP����
��G�Őڂ���悤�ɓ��ڂ��Ă���AP����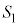 �̊O�ɏo�邱�Ƃ͂���܂���(2�~�̈ʒu�W���Q��)�B
�̊O�ɏo�邱�Ƃ͂���܂���(2�~�̈ʒu�W���Q��)�B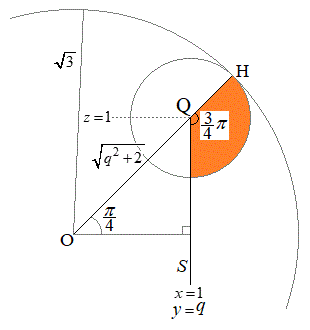 N��(1)�E��}�̐���AC��̓_Q
N��(1)�E��}�̐���AC��̓_Q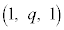 (
(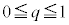 )�Ɉʒu����Ƃ�(�E�})�A
)�Ɉʒu����Ƃ�(�E�})�A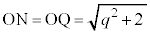 �Ȃ̂ŁA�@���A
�Ȃ̂ŁA�@���A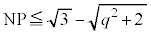 �ƂȂ�AP��N�𒆐S�Ƃ��锼�a
�ƂȂ�AP��N�𒆐S�Ƃ��锼�a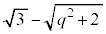 �̋�
�̋�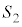 �����܂��B
�����܂��B
���̂Ƃ��A����OQ�ƁA���_�𒆐S�Ƃ��锼�a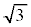 �̋��ʂƂ̌�_(2��_�̂���Q�ɋ߂���)��H�Ƃ��āAN������QH��Ɉʒu����Ƃ��AP��N�𒆐S�Ƃ��锼�a
�̋��ʂƂ̌�_(2��_�̂���Q�ɋ߂���)��H�Ƃ��āAN������QH��Ɉʒu����Ƃ��AP��N�𒆐S�Ƃ��锼�a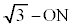 �̋����ɗ��܂����A���̋��́A���
�̋����ɗ��܂����A���̋��́A���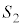 ��H�Őڂ���悤�ɓ��ڂ��Ă���AP����
��H�Őڂ���悤�ɓ��ڂ��Ă���AP����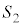 �̊O�ɏo�邱�Ƃ͂���܂���(2�~�̈ʒu�W���Q��)�B
�̊O�ɏo�邱�Ƃ͂���܂���(2�~�̈ʒu�W���Q��)�B
�ȏ���W��V����L���镔���ɂ��ẮAq��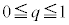 �͈̔͂ŕω����AN������AC��̓_Q
�͈̔͂ŕω����AN������AC��̓_Q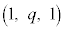 �ɗ����Ƃ��ɂł���N�𒆐S�Ƃ��锼�a
�ɗ����Ƃ��ɂł���N�𒆐S�Ƃ��锼�a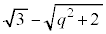 �̋��̂����AV����͂ݏo�镔�����ʉ߂��镔��T�̑̐ς����߂�悢���Ƃ��킩��܂��B
�̋��̂����AV����͂ݏo�镔�����ʉ߂��镔��T�̑̐ς����߂�悢���Ƃ��킩��܂��B
�E�}�̂悤�ɁA�O�p�`OAB���܂ޕ��ʂƁAS�̂���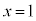 �ƂȂ�ʂƂ́A�p
�ƂȂ�ʂƂ́A�p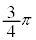 ���Ȃ����Ƃɒ��ӂ���ƁAV����͂ݏo�镔��T��y���ɐ����ȕ���
���Ȃ����Ƃɒ��ӂ���ƁAV����͂ݏo�镔��T��y���ɐ����ȕ���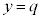 �Ő����f�ʂɂł���~��
�Ő����f�ʂɂł���~��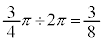 �̕����̖ʐς�ϕ����邱�ƂɂȂ�܂��B�܂��A
�̕����̖ʐς�ϕ����邱�ƂɂȂ�܂��B�܂��A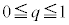 �ł̐ϕ���
�ł̐ϕ���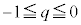 �ł̐ϕ����������A����BC��A�܂������`R�̑���3�ӂ��l���A
�ł̐ϕ����������A����BC��A�܂������`R�̑���3�ӂ��l���A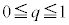 �͈̔͂Őϕ��������̂�8�{(���̑̐ς�
�͈̔͂Őϕ��������̂�8�{(���̑̐ς�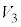 �Ƃ��܂�)���A(1)��V�̑̐ςƉ������킹��悢���ƂɂȂ�܂��B
�Ƃ��܂�)���A(1)��V�̑̐ςƉ������킹��悢���ƂɂȂ�܂��B
�ł����A���̑̐�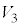 ���A
���A �Ƃ��Čv�Z���邱�Ƃ͂ł��܂���B�Ȃ��Ȃ�AN��C�ɗ����Ƃ�(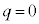 )�������āA����OQ�͕�AB�Ɛ����ł͂Ȃ��AT��
)�������āA����OQ�͕�AB�Ɛ����ł͂Ȃ��AT��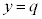 (��AB�Ɛ���)�Ő����Ƃ��ɂł���f�ʂ̉~�̔��a��
(��AB�Ɛ���)�Ő����Ƃ��ɂł���f�ʂ̉~�̔��a��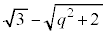 �ɂȂ�Ȃ��@���(��)�@����ł��BN��Q
�ɂȂ�Ȃ��@���(��)�@����ł��BN��Q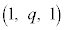 �ɗ����Ƃ��ɂł��锼�a
�ɗ����Ƃ��ɂł��锼�a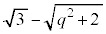 �̋�
�̋� �����ʂ̕������́A
�����ʂ̕������́A 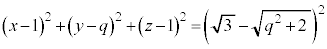 �@����A
�@����Aq��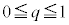 �ƕω�����Ƃ��ɇA�y�ѓ����̂�����
�ƕω�����Ƃ��ɇA�y�ѓ����̂�����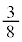 �̕������ʉ߂��Ăł��闧��T��y���ɐ����ȕ���
�̕������ʉ߂��Ăł��闧��T��y���ɐ����ȕ���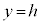 �Ő����Ƃ��̒f�ʂ̉~���l���܂��B�A��
�Ő����Ƃ��̒f�ʂ̉~���l���܂��B�A��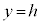 �Ƃ���ƁA
�Ƃ���ƁA �f�ʂ̉~�̕������́A
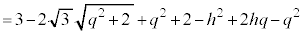
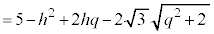 �@����C
�@����C�ƂȂ�A�f�ʂ̉~�̔��a��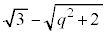 �ɂȂ�Ȃ����Ƃ��킩��܂��B�C�̉E�ӂ́A
�ɂȂ�Ȃ����Ƃ��킩��܂��B�C�̉E�ӂ́A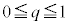 �͈̔͂ɂ���q�ɑ��Ăł���e���ʂ�
�͈̔͂ɂ���q�ɑ��Ăł���e���ʂ�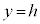 �Ő����Ƃ��̒f�ʂɂł���~�̔��a��2��ł����Ah���Œ肵�Ă��̒��ōő�ƂȂ���̂����߂܂��B
�Ő����Ƃ��̒f�ʂɂł���~�̔��a��2��ł����Ah���Œ肵�Ă��̒��ōő�ƂȂ���̂����߂܂��B �Ƃ����ƁA
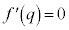 �Ƃ���ƁA
�Ƃ���ƁA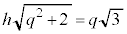 �C
�C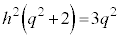 �C
�C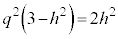 �C
�C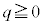 ���A
���A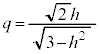
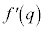 �́A
�́A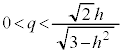 ��
��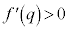 �C
�C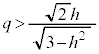 ��
��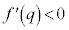 �ƂȂ�̂ŁA
�ƂȂ�̂ŁA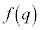 ��
��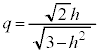 �ɂ����āA�ő�l
�ɂ����āA�ő�l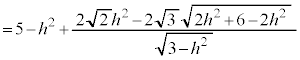
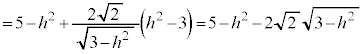 �@����D
�@����D���Ƃ�܂�(���̑������Q��)�B�܂�A����T��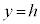 �Ő����Ƃ��ɂł���f�ʂ̉~�̔��a�́A
�Ő����Ƃ��ɂł���f�ʂ̉~�̔��a�́A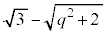 ���邢��
���邢��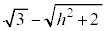 �ł͂Ȃ��A
�ł͂Ȃ��A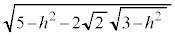 �ɂȂ�܂��B
�ɂȂ�܂��B 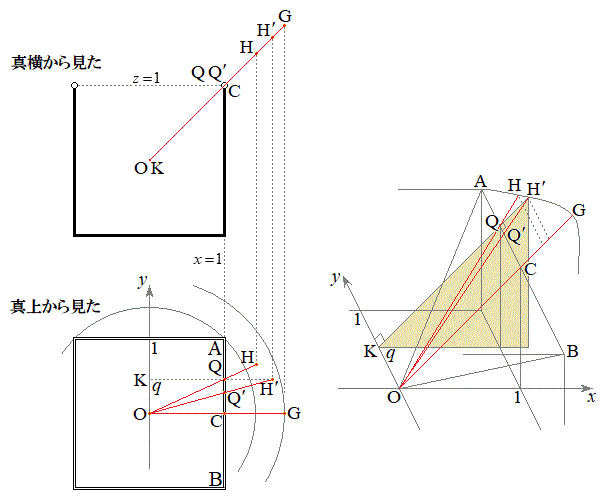 ���D��L��(��)�ɂ��Č������Ă݂܂��B�D�́A
���D��L��(��)�ɂ��Č������Ă݂܂��B�D�́A�Ə���������̂ł����A���̈Ӗ����l���܂��B�E�}�ɗ���T��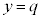 (
(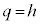 )�Ő����Ƃ��̏������܂��B�E�}�ŁAA�CH�C
)�Ő����Ƃ��̏������܂��B�E�}�ŁAA�CH�C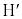 �CG�͋���Σ��̓_�ŁA
�CG�͋���Σ��̓_�ŁA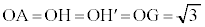 �ł��BQ
�ł��BQ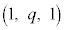 (
(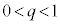 )��O�����Ԓ����Ƌ���Σ�Ƃ̌�_(2��_�̂���Q�ɋ߂���)��H�ł��B
)��O�����Ԓ����Ƌ���Σ�Ƃ̌�_(2��_�̂���Q�ɋ߂���)��H�ł��B
�E���̘��Ղ����}�ŁAQ��ʂ�y���ɐ����ȕ���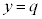 �𔖉��F�Ŏ����܂����B���̖ʂŗ���T������f�ʂ��l���Ă��܂��B���̐}������ƁA����OH��y���Ɛ����łȂ��̂ŁA
�𔖉��F�Ŏ����܂����B���̖ʂŗ���T������f�ʂ��l���Ă��܂��B���̐}������ƁA����OH��y���Ɛ����łȂ��̂ŁA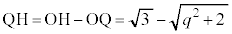 ������
������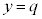 ��ɗ��Ȃ����Ƃ�������܂��B�E�̘��Ր}�ł́AQ�������C���̐���CA��̓_
��ɗ��Ȃ����Ƃ�������܂��B�E�̘��Ր}�ł́AQ�������C���̐���CA��̓_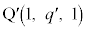 ��O�����Ԓ����Ƌ���Σ�Ƃ̌�_(2��_�̂���
��O�����Ԓ����Ƌ���Σ�Ƃ̌�_(2��_�̂���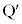 �ɋ߂���)��
�ɋ߂���)��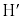 �ŁA����
�ŁA����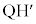 ��y���Ɛ����ɂȂ��Ă��܂��B����
��y���Ɛ����ɂȂ��Ă��܂��B����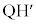 �́A����
�́A����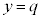 ��ɂ���A����T��
��ɂ���A����T��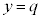 �Ő����Ƃ��ɒf�ʂɂł���~�̔��a�ɂȂ��Ă��܂��B��L�ł͔������āA
�Ő����Ƃ��ɒf�ʂɂł���~�̔��a�ɂȂ��Ă��܂��B��L�ł͔������āA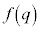 ��
��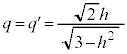 �̂Ƃ��ő�l
�̂Ƃ��ő�l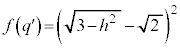 ���Ƃ邱�Ƃ����߂܂������A�E�}�ŁA����
���Ƃ邱�Ƃ����߂܂������A�E�}�ŁA����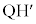 ��y���Ƃ̌�_��K�Ƃ���ƁA
��y���Ƃ̌�_��K�Ƃ���ƁA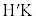 ��y���Ɛ����Ȃ̂ŁA
��y���Ɛ����Ȃ̂ŁA �������āA�D���A�f�ʂ̉~�̖ʐς�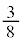 ��ϕ����A
��ϕ����A 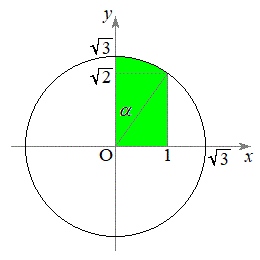
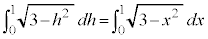 �́A
�́A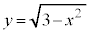 �C�܂�A
�C�܂�A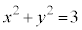 ��x���̊Ԃ�
��x���̊Ԃ�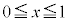 �̕���(�E�}���ΐF���F��)�̖ʐςƌ��āA���a
�̕���(�E�}���ΐF���F��)�̖ʐςƌ��āA���a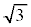 �̉~�̖ʐς�
�̉~�̖ʐς�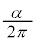 �̕���
�̕���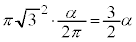 �ƁA���1����
�ƁA���1����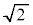 �̎O�p�`�̖ʐ�
�̎O�p�`�̖ʐ�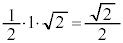 �̘a�Ƃ���
�̘a�Ƃ���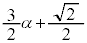 (�u���ϕ�(����2)���Q��)�C����āA
(�u���ϕ�(����2)���Q��)�C����āA���߂�̐ς́A(1)�̌��ʂ��A
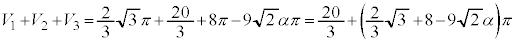 ......[��]
......[��]
�y�L���z��������L���ł��B�����̊F���܂̂��x�������������肽���A��낵�����肢�������܂��B
�y�L���z�L���͂����܂łł��B
�@�@���嗝�n���wTOP�@�@���wTOP�@�@TOP�y�[�W�ɖ߂�
�y�L���z��������L���ł��B�����̊F���܂̂��x�������������肽���A��낵�����肢�������܂��B
�y�L���z�L���͂����܂łł��B
�e���̒��쌠��
�o���w�ɑ����܂��B©2005-2024(�L)����� ��w�y�w�m ���������t���I���n��w�l�b�g�m��w�y�w�m(���ē���������)������́A
�܂��A������܂Ń��[����
�����肭�������B 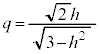
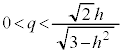 ��
��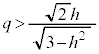 ��
��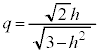 �ɂ����āA�ő�l
�ɂ����āA�ő�l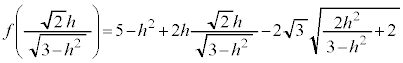
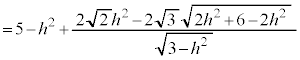
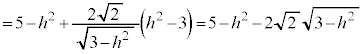 �@����D
�@����D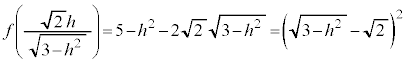
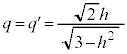 �̂Ƃ��ő�l
�̂Ƃ��ő�l