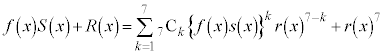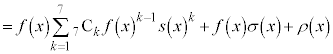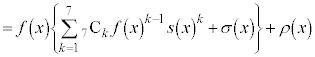���嗝�n���w'23�N�O��[5]
����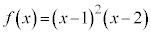 ���l����B
���l����B
(1) 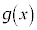 ���������W���Ƃ��鐮���Ƃ��A
���������W���Ƃ��鐮���Ƃ��A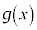 ��
��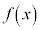 �Ŋ������]���
�Ŋ������]���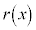 �Ƃ����B
�Ƃ����B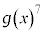 ��
��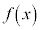 �Ŋ������]���
�Ŋ������]���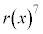 ��
��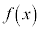 �Ŋ������]�肪���������Ƃ������B
�Ŋ������]�肪���������Ƃ������B (2) a�Cb�������Ƃ��A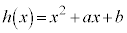 �Ƃ����B
�Ƃ����B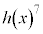 ��
��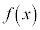 �Ŋ������]���
�Ŋ������]���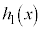 �Ƃ����A
�Ƃ����A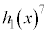 ��
��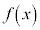 �Ŋ������]���
�Ŋ������]���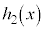 �Ƃ����B
�Ƃ����B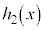 ��
��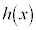 �ɓ������Ȃ�悤��a�Cb�̑g�����ׂċ��߂�B
�ɓ������Ȃ�悤��a�Cb�̑g�����ׂċ��߂�B
�y�L���z��������L���ł��B�����̊F���܂̂��x�������������肽���A��낵�����肢�������܂��B
�y�L���z�L���͂����܂łł��B
���@��蕶��ǂ�łт����肳�����܂����A����͓��吔�w��1�̓����ŁA����ȏɂ�����Ă���Âɘ_���I�ɖ������ɓ�����邩�A�Ƃ������������悤�Ƃ��Ă���̂ł��B�|���C�Â��悤�ł͓��升�i�͖]�߂܂���B
(1) 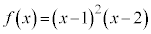 ���A
���A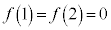 �@����@�@(�����藝���Q��)
�@����@�@(�����藝���Q��) 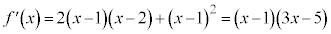 ���A
���A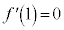 �@����A
�@����A
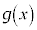 ��
��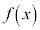 �Ŋ���������
�Ŋ���������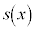 �C�]���
�C�]���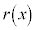 �Ƃ����ƁA
�Ƃ����ƁA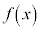 ��3�����Ȃ̂ŁA
��3�����Ȃ̂ŁA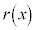 ��2�����ł��B�B����������ƁA
��2�����ł��B�B����������ƁA�B��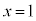 �Ƃ��āA�@���A
�Ƃ��āA�@���A 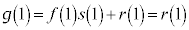 �@����D
�@����D�B��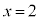 �Ƃ��āA�@���A
�Ƃ��āA�@���A 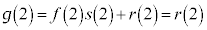 �@����E
�@����E�C��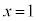 �Ƃ��āA�@�C�A���A
�Ƃ��āA�@�C�A���A 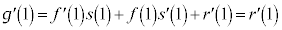 �@����F
�@����F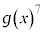 ��
��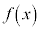 �Ŋ���������
�Ŋ���������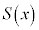 �C�]���
�C�]���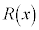 �Ƃ����ƁA
�Ƃ����ƁA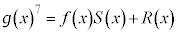 �@����G
�@����G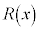 ��
��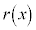 �Ɠ��l2�����ŁA�B���A
�Ɠ��l2�����ŁA�B���A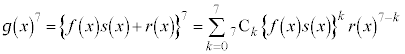
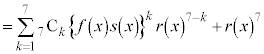 �@����H
�@����H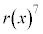 ��
��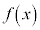 �Ŋ���������
�Ŋ���������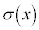 �C�]���
�C�]���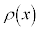 �Ƃ����ƁA
�Ƃ����ƁA����ƇG�C�H���A
�����ʓ���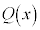 �Ƃ����ƁA
�Ƃ����ƁA 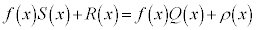 �@����I
�@����I���ӂ��������ƁA
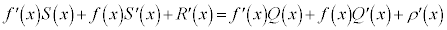 �@����J
�@����J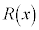 �C
�C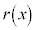 ��2�����ŁAA�CB�CC�Ca�Cb�Cc�������Ƃ��A
��2�����ŁAA�CB�CC�Ca�Cb�Cc�������Ƃ��A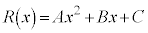 �C
�C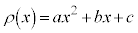 �Ƃ����ƁA
�Ƃ����ƁA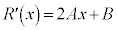 �C
�C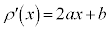
�I��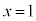 �Ƃ���ƁA�@���
�Ƃ���ƁA�@���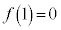 �Ȃ̂ŁA
�Ȃ̂ŁA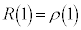 �@��
�@�� 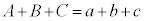 �@����K
�@����K�I��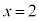 �Ƃ���ƁA�@���
�Ƃ���ƁA�@���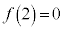 �Ȃ̂ŁA
�Ȃ̂ŁA 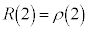 �@��
�@�� 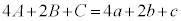 �@����L
�@����L�J��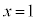 �Ƃ���ƁA�A���
�Ƃ���ƁA�A���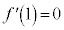 �C�܂��@��p���āA
�C�܂��@��p���āA 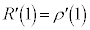 �@��
�@�� 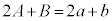 �@����M
�@����M�M���L�ɑ�����āA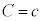 �C����ƇK���A
�C����ƇK���A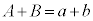 �C����ɇM���A
�C����ɇM���A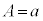 �C����āA
�C����āA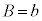 �@��
�@�� 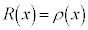 ����āA
����āA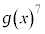 ��
��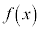 �Ŋ������]���
�Ŋ������]���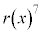 ��
��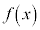 �Ŋ������]�肪���������Ƃ�������܂����B
�Ŋ������]�肪���������Ƃ�������܂����B ���D��L�ł́A�]���2������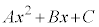 �C
�C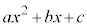 �Ƌ�̓I�ɂ����čl���܂������A��̓I�ɂ����Ȃ��Ă��A
�Ƌ�̓I�ɂ����čl���܂������A��̓I�ɂ����Ȃ��Ă��A 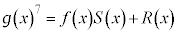 ��
��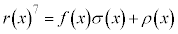 �̍����Ƃ�A
�̍����Ƃ�A�����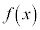 �Ŋ�����̂ŁA
�Ŋ�����̂ŁA ��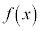 �Ŋ����āA
�Ŋ����āA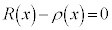 �C�����A
�C�����A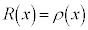
�Ƃ��邱�Ƃ��ł��܂��B
(2) 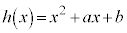 ���A
���A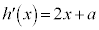 �C
�C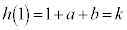 �C
�C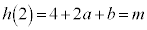 �C
�C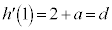 (k�Cm�Cd�͎���)�@����N�@�Ƃ����܂��B
(k�Cm�Cd�͎���)�@����N�@�Ƃ����܂��B 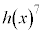 ��3����
��3����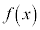 �Ŋ���������
�Ŋ���������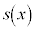 �C�]���2������
�C�]���2������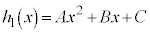 �� (A�CB�CC�͎���)����ƁA
�� (A�CB�CC�͎���)����ƁA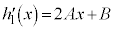
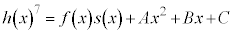 �@����O
�@����O���ӂ��������ƁA
�O��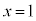 �C
�C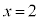 �Ƃ���ƁA�N���
�Ƃ���ƁA�N���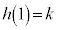 �C
�C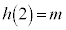 �C�܂��@���
�C�܂��@���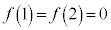 �ŁA
�ŁA 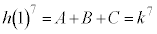 �@����Q
�@����Q
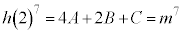 �@����R
�@����R�P��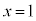 �Ƃ���ƁA�N���
�Ƃ���ƁA�N���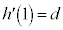 �C�܂��A���
�C�܂��A���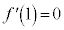 �ŁA
�ŁA 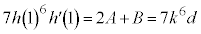 �@����S
�@����S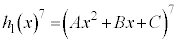 ��
��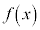 �Ŋ���������
�Ŋ���������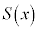 �C�]���
�C�]���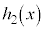 �Ƃ���ƁA
�Ƃ���ƁA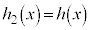 ���A
���A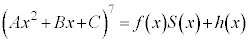 �@���(21)
�@���(21)(21)��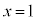 �Ƃ���ƁA
�Ƃ���ƁA 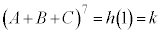 �@���(22)
�@���(22)(21)��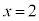 �Ƃ���ƁA
�Ƃ���ƁA 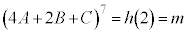 �@���(23)
�@���(23)(21)���ӂ��������ƁA
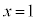 �Ƃ���ƁA
�Ƃ���ƁA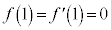 �C�N���A
�C�N���A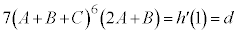 �@���(24)
�@���(24)�Q��(22)�ɑ������ƁA
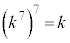 �@��
�@�� 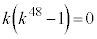
k�͎����Ȃ̂ŁA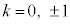
�E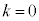 �̂Ƃ��A�N�C�Q���
�̂Ƃ��A�N�C�Q���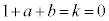 �C
�C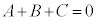 �ŁA(22)�͖�������A�����(24)���A
�ŁA(22)�͖�������A�����(24)���A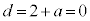
����āA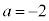 �C
�C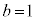 �C�N���A
�C�N���A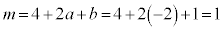
�R���A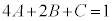 �C(23)�͖�������A�S���A
�C(23)�͖�������A�S���A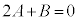 �ŁA(24)�̍��ӂ�0�C(24)�̉E�ӂ�0�ŁA(24)����������܂��B����āA
�ŁA(24)�̍��ӂ�0�C(24)�̉E�ӂ�0�ŁA(24)����������܂��B����āA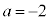 �C
�C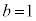 �͓K�B�@���(25)
�͓K�B�@���(25) �E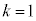 �̂Ƃ��A�N�C�Q�C�S���
�̂Ƃ��A�N�C�Q�C�S���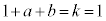 �C
�C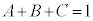 �C
�C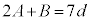 �ŁA�����(24)���A
�ŁA�����(24)���A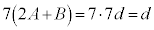 �@��
�@�� 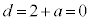
����āA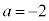 �C
�C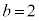 �C
�C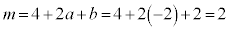
�R���A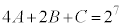 �ł����A(23)�̍��ӂ�
�ł����A(23)�̍��ӂ�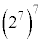 �C�E�ӂ�2�ƂȂ�A(23)�����������A�s�K�ł��B
�C�E�ӂ�2�ƂȂ�A(23)�����������A�s�K�ł��B �E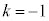 �̂Ƃ��A�N�C�Q�C�S���
�̂Ƃ��A�N�C�Q�C�S���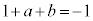 �C
�C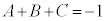 �C
�C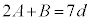 �ŁA�����(24)���A
�ŁA�����(24)���A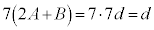 �@��
�@�� 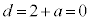
����āA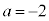 �C
�C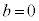 �C
�C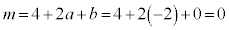
�R���A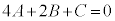 �ŁA(23)���������܂��B(22)�́A���ӂ��E�ӂ�
�ŁA(23)���������܂��B(22)�́A���ӂ��E�ӂ�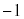 �Ő������܂��B
�Ő������܂��B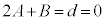 �Ȃ̂�(24)���������܂��B����āA
�Ȃ̂�(24)���������܂��B����āA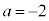 �C
�C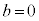 �͓K�B�@���(26)
�͓K�B�@���(26) (25)�C(26)���A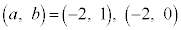 ......[��]
......[��]
���D��L�́A���� ��3����
��3����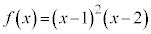 �Ŋ���ƁA�]���2����
�Ŋ���ƁA�]���2����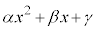 �ł����āA
�ł����āA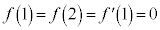 ���A
���A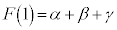 �C
�C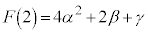 �C
�C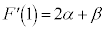 �ɂȂ�A�Ƃ������Ƃ�p���ĉ��Ă��܂����A�\�������S�z�ȕ��̂��߂Ɋm���߂����Ă����܂��B
�ɂȂ�A�Ƃ������Ƃ�p���ĉ��Ă��܂����A�\�������S�z�ȕ��̂��߂Ɋm���߂����Ă����܂��B 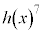 ��
��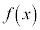 �Ŋ������]���
�Ŋ������]���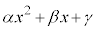 �Ƃ����ƁA
�Ƃ����ƁA
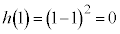 �ŁA
�ŁA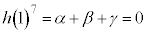
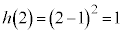 �ŁA
�ŁA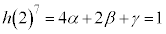
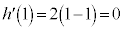 �ŁA
�ŁA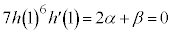
������A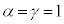 �C
�C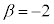 �C�܂�A
�C�܂�A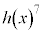 ��
��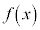 �Ŋ������]���
�Ŋ������]���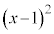 ��
��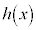 �ł��B�]���āA�]���
�ł��B�]���āA�]���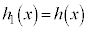 ��7��
��7��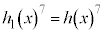 ��
��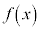 �Ŋ������]���
�Ŋ������]���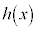 �ł��B
�ł��B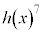 ��
��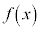 �Ŋ������]���
�Ŋ������]���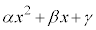 �Ƃ����ƁA
�Ƃ����ƁA
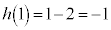 �ŁA
�ŁA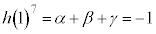
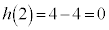 �ŁA
�ŁA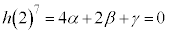
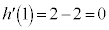 �ŁA
�ŁA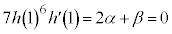
������A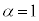 �C
�C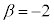 �C
�C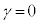 �C�܂�A
�C�܂�A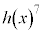 ��
��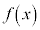 �Ŋ������]���
�Ŋ������]���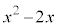 ��
��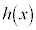 �ł��B�]���āA�]���
�ł��B�]���āA�]���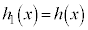 ��7��
��7��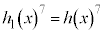 ��
��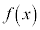 �Ŋ������]���
�Ŋ������]���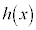 �ł��B
�ł��B������̏ꍇ���A��������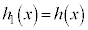 �Ȃ̂�
�Ȃ̂�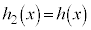 �ɂȂ��Ă���킯�ł��B
�ɂȂ��Ă���킯�ł��B
�y�L���z��������L���ł��B�����̊F���܂̂��x�������������肽���A��낵�����肢�������܂��B
�y�L���z�L���͂����܂łł��B
�@�@���嗝�n���wTOP�@�@���wTOP�@�@TOP�y�[�W�ɖ߂�
�y�L���z��������L���ł��B�����̊F���܂̂��x�������������肽���A��낵�����肢�������܂��B
�y�L���z�L���͂����܂łł��B
�e���̒��쌠��
�o���w�ɑ����܂��B©2005-2024(�L)����� ��w�y�w�m ���������t���I���n��w�l�b�g�m��w�y�w�m(���ē���������)������́A
�܂��A������܂Ń��[����
�����肭�������B 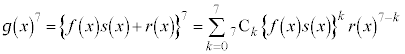
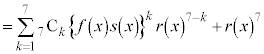 �@����H
�@����H