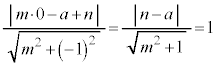���嗝�n���w'23�N�O��[3]
a�������Ƃ��A���W���ʏ�̓_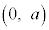 �𒆐S�Ƃ��锼�a1�̉~�̎���C�Ƃ���B
�𒆐S�Ƃ��锼�a1�̉~�̎���C�Ƃ���B
(1) C���A�s����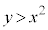 �̕\���̈�Ɋ܂܂��悤��a�͈̔͂����߂�B
�̕\���̈�Ɋ܂܂��悤��a�͈̔͂����߂�B (2) a��(1)�ŋ��߂��͈͂ɂ���Ƃ���BC�̂���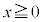 ����
����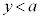 ����������S�Ƃ���BS��̓_P�ɑ��A�_P�ł�C�̐ڐ���������
����������S�Ƃ���BS��̓_P�ɑ��A�_P�ł�C�̐ڐ���������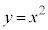 �ɂ���Đ����Ăł�������̒�����
�ɂ���Đ����Ăł�������̒�����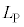 �Ƃ���B
�Ƃ���B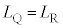 �ƂȂ�S��̑��قȂ�2�_Q�CR�����݂���悤��a�͈̔͂����߂�B
�ƂȂ�S��̑��قȂ�2�_Q�CR�����݂���悤��a�͈̔͂����߂�B
�y�L���z��������L���ł��B�����̊F���܂̂��x�������������肽���A��낵�����肢�������܂��B
�y�L���z�L���͂����܂łł��B
���@�v�Z�G�������Ȃ��悤�ɁA�ǂ�ǂ�ϐ���u�������Ă����H�v���K�v�ł��B�Ȃ��A2�����A�~�ƕ������̈ʒu�W���Q�Ƃ��Ă��������B
(1) C���A�s����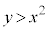 �̕\���̈��Ɋ܂܂��Ƃ��A�Ȑ�
�̕\���̈��Ɋ܂܂��Ƃ��A�Ȑ�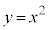 ��̑S�Ă̓_
��̑S�Ă̓_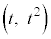 (t�F����)��
(t�F����)��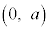 �Ƃ̋�����1���傫���Ȃ�܂��B����āA
�Ƃ̋�����1���傫���Ȃ�܂��B����āA ���ꂪ�S�Ă̎���t �Ő������邽�߂ɂ́A���ӂ�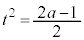 �ōŏ��l
�ōŏ��l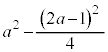 ���Ƃ�(2�����̍ő�E�ŏ����Q��)�̂ŁA
���Ƃ�(2�����̍ő�E�ŏ����Q��)�̂ŁA �܂�A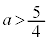 �ł��邱�Ƃ��K�v�\���ł��B
�ł��邱�Ƃ��K�v�\���ł��B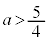 ......[��]
......[��] �ʉ��D�������F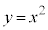 ���@�����l���܂��B
���@�����l���܂��B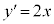 �C
�C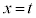 �ɂ�����@���̌X����
�ɂ�����@���̌X����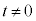 �ł���A
�ł���A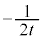
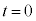 �̂Ƃ��A
�̂Ƃ��A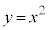 ��
��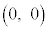 �ɂ�����@����y���A����
�ɂ�����@����y���A����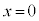 �ŁA���̖@���͓_
�ŁA���̖@���͓_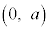 ��ʂ�܂��B
��ʂ�܂��B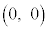 ��
��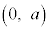 �Ƃ̋�����a�ŁA���̋�����1���傫���Ƃ��A���Ȃ��Ƃ�
�Ƃ̋�����a�ŁA���̋�����1���傫���Ƃ��A���Ȃ��Ƃ�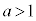 �@����@
�@����@
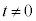 �̂Ƃ��A
�̂Ƃ��A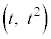 �ɂ�����@���́A
�ɂ�����@���́A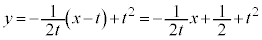
���ꂪ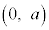 ��ʂ�Ƃ��A
��ʂ�Ƃ��A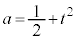
�@��菭�Ȃ��Ƃ�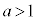 �Ȃ̂ŁA
�Ȃ̂ŁA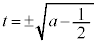
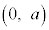 ��
��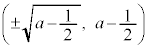 �Ƃ̋�����1���傫���̂ŁA
�Ƃ̋�����1���傫���̂ŁA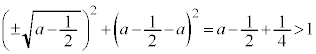 �@��
�@�� 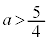
(2) �~C�̐ڐ���C�Ƃ̐ړ_��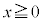 �C
�C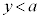 �͈̔͂ɂ���(�ړ_��x���W�́A
�͈̔͂ɂ���(�ړ_��x���W�́A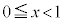 )�̂ŁA�ڐ���x���ɐ����ɂȂ邱�Ƃ͂Ȃ��A�ڐ��̌X��m��
)�̂ŁA�ڐ���x���ɐ����ɂȂ邱�Ƃ͂Ȃ��A�ڐ��̌X��m��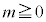 �͈̔͂ɂ���A�ڐ���
�͈̔͂ɂ���A�ڐ���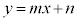 �Ƃ������Ƃ��ł��܂��B
�Ƃ������Ƃ��ł��܂��B ����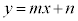 ���~C�̐ڐ��ł��邽�߂ɁA�~C�̒��S
���~C�̐ڐ��ł��邽�߂ɁA�~C�̒��S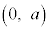 �ƒ����Ƃ̋�����1 (�~�ƒ����̈ʒu�W���Q��)�ł��B�܂�A
�ƒ����Ƃ̋�����1 (�~�ƒ����̈ʒu�W���Q��)�ł��B�܂�A �܂��A�ړ_��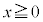 �C
�C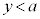 �͈̔͂ɂ��邱�Ƃ���A������y�ؕЂ�a�����������A
�͈̔͂ɂ��邱�Ƃ���A������y�ؕЂ�a�����������A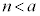 �C
�C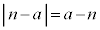 �C�]���āA
�C�]���āA 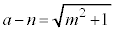 �@��
�@�� 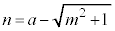 �@����@
�@����@�ڐ��̎�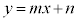 �ƕ������̎�
�ƕ������̎�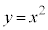 ��A������ƁA
��A������ƁA �ڐ���x���ɐ����ɂȂ邱�Ƃ͂Ȃ��A�ڐ��ƕ������͕K��2��_�����̂ŁA����2���������͑��قȂ�2�������������܂��B����2��������α�Cβ�Ƃ���(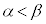 )�ƁA���ƌW���̊W���A
)�ƁA���ƌW���̊W���A 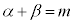 �C
�C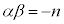 �@����A
�@����A�_P�ł�C�̐ڐ���������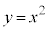 �ɂ���Đ����Ăł�������̒���
�ɂ���Đ����Ăł�������̒���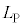 �́A���������2�_
�́A���������2�_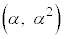 �C
�C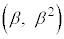 �̋����ł����āA����2��́A
�̋����ł����āA����2��́A �Ƃ����ƁA
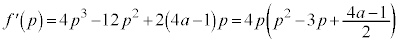 �@����B
�@����B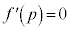 �Ƃ���ƁA
�Ƃ���ƁA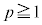 �ɂ����Ă�
�ɂ����Ă�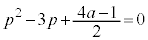 2��������
2��������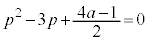 �̔��ʎ��F
�̔��ʎ��F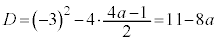
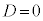 �Ƃ���ƁA
�Ƃ���ƁA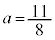 (
(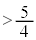 )
)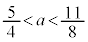 �ɂ����Ă�
�ɂ����Ă�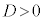 �ł����A
�ł����A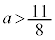 �ɂȂ��
�ɂȂ��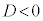 �ł��B�����ŁAa�̒l�ɂ��ďꍇ�������܂��B
�ł��B�����ŁAa�̒l�ɂ��ďꍇ�������܂��B(i) 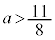 �̂Ƃ��A�B���A
�̂Ƃ��A�B���A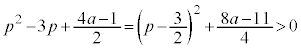
���̂Ƃ��A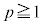 �ɂ�����
�ɂ�����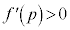 ���A
���A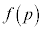 ��p�ɂ����P�������ł��B
��p�ɂ����P�������ł��B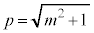 ��m�ɂ��ĒP�������A�ڐ��̌X��m�͐ړ_P��x���W(
��m�ɂ��ĒP�������A�ڐ��̌X��m�͐ړ_P��x���W(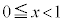 )�ɂ��ĒP���������A
)�ɂ��ĒP���������A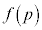 �͐ړ_P��x���W�ɑ��ĒP���ł���A
�͐ړ_P��x���W�ɑ��ĒP���ł���A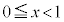 �͈̔͂ɂ���قȂ�2��x�ɂ���
�͈̔͂ɂ���قȂ�2��x�ɂ���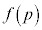 �̊��l���������Ȃ邱�Ƃ͂���܂���B���(��)
�̊��l���������Ȃ邱�Ƃ͂���܂���B���(��) (ii) 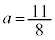 �̂Ƃ����A
�̂Ƃ����A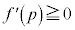 �ł����āA
�ł����āA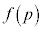 �͒P�������ŁA���̏ꍇ���قȂ�2��x�ɂ��Ċ��l���������Ȃ邱�Ƃ͂���܂���B
�͒P�������ŁA���̏ꍇ���قȂ�2��x�ɂ��Ċ��l���������Ȃ邱�Ƃ͂���܂���B (iii) 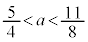 �̂Ƃ��A�B���A
�̂Ƃ��A�B���A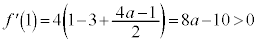 �C
�C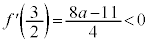 �C
�C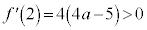 ���A
���A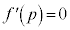 �́A
�́A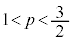 �C
�C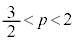 �͈̔͂ɁA���ꂼ�������γ�Cδ�������܂�(
�͈̔͂ɁA���ꂼ�������γ�Cδ�������܂�(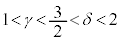 )�B�����\�͈ȉ�(���̑������Q��)�B
)�B�����\�͈ȉ�(���̑������Q��)�B �����\���A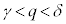 �����C�ӂ�
�����C�ӂ�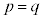 �ɂ��āA
�ɂ��āA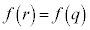 �C
�C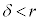 �ƂȂ�
�ƂȂ�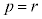 ���K�����݂��܂��B���̂Ƃ��A
���K�����݂��܂��B���̂Ƃ��A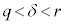 �ł���A
�ł���A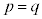 �ɑΉ�����ړ_Q�C
�ɑΉ�����ړ_Q�C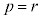 �ɑΉ�����ړ_R�ɂ��āA
�ɑΉ�����ړ_R�ɂ��āA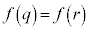 �C�����A
�C�����A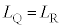 �ƂȂ�܂��B�܂�A
�ƂȂ�܂��B�܂�A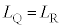 �ƂȂ�S��̑��قȂ�2�_Q�CR�����݂��܂��B
�ƂȂ�S��̑��قȂ�2�_Q�CR�����݂��܂��B ����āA���߂�a�͈̔͂́A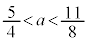 ......[��]
......[��]
�y�L���z��������L���ł��B�����̊F���܂̂��x�������������肽���A��낵�����肢�������܂��B
�y�L���z�L���͂����܂łł��B
�@�@���嗝�n���wTOP�@�@���wTOP�@�@TOP�y�[�W�ɖ߂�
�y�L���z��������L���ł��B�����̊F���܂̂��x�������������肽���A��낵�����肢�������܂��B
�y�L���z�L���͂����܂łł��B
�e���̒��쌠��
�o���w�ɑ����܂��B©2005-2024(�L)����� ��w�y�w�m ���������t���I���n��w�l�b�g�m��w�y�w�m(���ē���������)������́A
�܂��A������܂Ń��[����
�����肭�������B 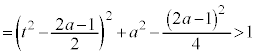
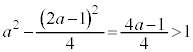
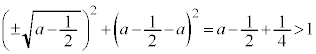 �@��
�@��