���嗝�H���w'06�N[1]
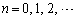 �ɑ��āA��
�ɑ��āA��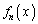 ��
��
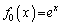 �C
�C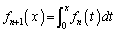
(1) 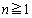 �ɂ�������
�ɂ������� �������B
(2) 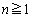 �Ƃ���B
�Ƃ���B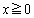 �ɑ��āA�s����
�ɑ��āA�s���� �������B
(3) 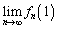 �����߂�B
�����߂�B
�y�L���z��������L���ł��B�����̊F���܂̂��x�������������肽���A��낵�����肢�������܂��B
�y�L���z�L���͂����܂łł��B
(I) 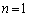 �̂Ƃ��A
�̂Ƃ��A �� 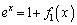 ����āA�^���͐��藧���܂��B
����āA�^���͐��藧���܂��B
(II) 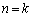 �̂Ƃ��A�^�������藧�Ɖ��肵�܂��B
�̂Ƃ��A�^�������藧�Ɖ��肵�܂��B �� 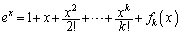
(I)�C(II)���A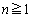 �ɑ��āA
�ɑ��āA �����藧���܂��B
(I) (1)���A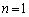 �̂Ƃ��A
�̂Ƃ��A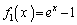
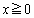 �ɂ����āA
�ɂ����āA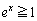 ���A
���A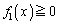 ����@
����@
�܂��A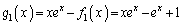 �Ƃ����ƁA
�Ƃ����ƁA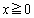 �ɂ����āA
�ɂ����āA�� 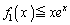 �@����A
�@����A
�@�C�A���A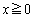 �ɂ����āA
�ɂ����āA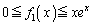
����āA�^�s�����͐��藧���܂��B
(II) 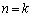 �̂Ƃ��A�^�s���������������Ƃ��܂��B
�̂Ƃ��A�^�s���������������Ƃ��܂��B 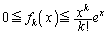 �@(
�@(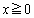 )�@����B
)�@����B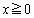 �ɂ����āA
�ɂ����āA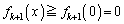 �@����C
�@����C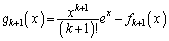 �Ƃ����ƁA
�Ƃ����ƁA
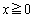 �ɂ����āA�B���A
�ɂ����āA�B���A�� 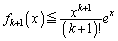 �@����D
�@����D
�C�C�D���A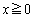 �ɂ����āA
�ɂ����āA ����āA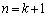 �̂Ƃ����A�^�s�����͐��藧���܂��B
�̂Ƃ����A�^�s�����͐��藧���܂��B (I)�C(II)���A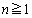 �Ƃ��āA
�Ƃ��āA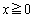 �ɑ��āA�s����
�ɑ��āA�s���� �����藧���܂��B
(3) (2)�̕s�����ɂ����āA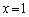 �Ƃ���ƁA
�Ƃ���ƁA
�y�L���z��������L���ł��B�����̊F���܂̂��x�������������肽���A��낵�����肢�������܂��B
�y�L���z�L���͂����܂łł��B
�@�@���嗝�H���wTOP�@�@���wTOP�@�@TOP�y�[�W�ɖ߂�
�y�L���z��������L���ł��B�����̊F���܂̂��x�������������肽���A��낵�����肢�������܂��B
�y�L���z�L���͂����܂łł��B
�e���̒��쌠��
�o���w�ɑ����܂��B©2005-2024(�L)����� ��w�y�w�m ���������t���I���n��w�l�b�g�m��w�y�w�m(���ē���������)������́A
�܂��A������܂Ń��[����
�����肭�������B