早稲田大学基幹・創造・先進理工学部2020年数学入試問題
【広告】ここから広告です。ご覧の皆さまのご支援ご理解を賜りたく、よろしくお願いいたします。
【広告】広告はここまでです。
[1] 複素数α,β,γが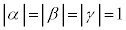 かつ
かつ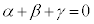 を満たすとき、以下の問に答えよ。
を満たすとき、以下の問に答えよ。
(1) α,β,γを表す複素平面上の点が正三角形をなすことを示せ。
(2) 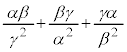 の値を求めよ。
の値を求めよ。 (3) nを3で割り切れない自然数とするとき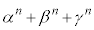 の値を求めよ。
の値を求めよ。 [解答へ]
[2] 放物線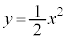 をCとする。C上を動く点をP
をCとする。C上を動く点をP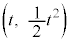 とし、dを正の定数とする。点PにおいてCに接する半径dの円で、中心Qの座標
とし、dを正の定数とする。点PにおいてCに接する半径dの円で、中心Qの座標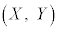 が
が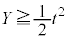 を満たすものを考える。このとき、以下の問に答えよ。
を満たすものを考える。このとき、以下の問に答えよ。
(1) 放物線CのPにおける接線の方程式を求めよ。
(2) 放物線CのPにおける法線の方程式を求めよ。
(3) 中心Qのy座標Yをtを用いて表せ。
(4) Yの極小値を求めよ。
[解答へ]
[3] 曲線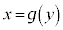 の
の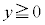 の部分とx軸上の線分
の部分とx軸上の線分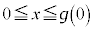 のなす曲線をCとし、Cをy軸のまわりに1回転してできる容器をVとする。ただし、
のなす曲線をCとし、Cをy軸のまわりに1回転してできる容器をVとする。ただし、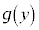 は
は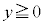 で定義された正の関数とする。Vに毎秒一定量vの水を注ぐとする。t秒後のV内の水位を
で定義された正の関数とする。Vに毎秒一定量vの水を注ぐとする。t秒後のV内の水位を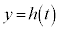 とするとき、以下の問に答えよ。
とするとき、以下の問に答えよ。
(1) 水位が一定の速さで上昇するとき、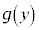 は定数関数であることを示せ。
は定数関数であることを示せ。 (2) 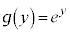 のとき、
のとき、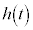 を求めよ。
を求めよ。 [解答へ]
[4] 箱の中にa個の赤玉とb個の白玉を合わせて2020個入れる。ただし、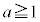 ,
,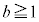 とする。n人を一列に並べ、前から順に1, 2, ・・・, nと番号をつける。番号1の人から順に玉を1個取り出し、色を確認したら箱の中へ戻し最後尾に並び直す。これを赤玉が出るまで繰り返す。番号kの人が赤玉を引く確率を
とする。n人を一列に並べ、前から順に1, 2, ・・・, nと番号をつける。番号1の人から順に玉を1個取り出し、色を確認したら箱の中へ戻し最後尾に並び直す。これを赤玉が出るまで繰り返す。番号kの人が赤玉を引く確率を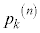 ,また、
,また、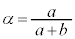 ,
,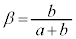 とするとき、以下の問に答えよ。
とするとき、以下の問に答えよ。
(1) 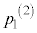 をβを用いて表せ。
をβを用いて表せ。 (2) 各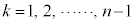 に対して、
に対して、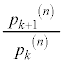 を求めよ。
を求めよ。 (3) 各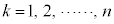 に対して
に対して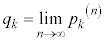 とし、
とし、 と定める。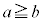 のとき、Eの値を最大にするようなa,bを求めよ。必要ならば、
のとき、Eの値を最大にするようなa,bを求めよ。必要ならば、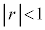 なる実数rに対して
なる実数rに対して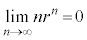 となることを用いてよい。
となることを用いてよい。 [解答へ]
[5] 以下の問に答えよ。
(1) 関数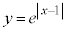 のグラフと関数
のグラフと関数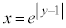 のグラフを一つの座標平面上に描け。
のグラフを一つの座標平面上に描け。 (2) 連立不等式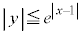 ,
,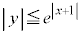 ,
,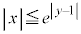 ,
,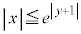 の表す領域をDとする。このとき、Dを図示せよ。
の表す領域をDとする。このとき、Dを図示せよ。 (3) 領域Dの面積を求めよ。
(4) 領域Dをx軸のまわりに1回転してできる回転体の体積を求めよ。
[解答へ]
【広告】ここから広告です。ご覧の皆さまのご支援ご理解を賜りたく、よろしくお願いいたします。
【広告】広告はここまでです。
早大理工数学TOP 数学TOP TOPページに戻る
【広告】ここから広告です。ご覧の皆さまのご支援ご理解を賜りたく、よろしくお願いいたします。
【広告】広告はここまでです。
各問題の著作権は
出題大学に属します。©2005-2024(有)りるらる 苦学楽学塾 随時入会受付中!理系大学受験ネット塾苦学楽学塾(ご案内はこちら)ご入会は、
まず、こちらまでメールを
お送りください。 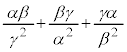 の値を求めよ。
の値を求めよ。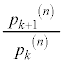 を求めよ。
を求めよ。