���嗝�H���w'20�N[3]
�Ȑ�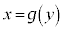 ��
��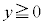 �̕�����x����̐���
�̕�����x����̐���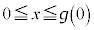 �̂Ȃ��Ȑ���C�Ƃ��AC��y���̂܂���1��]���Ăł���e���V�Ƃ���B�������A
�̂Ȃ��Ȑ���C�Ƃ��AC��y���̂܂���1��]���Ăł���e���V�Ƃ���B�������A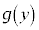 ��
��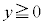 �Œ�`���ꂽ���̊��Ƃ���BV�ɖ��b����v�̐��𒍂��Ƃ���Bt�b���V���̐��ʂ�
�Œ�`���ꂽ���̊��Ƃ���BV�ɖ��b����v�̐��𒍂��Ƃ���Bt�b���V���̐��ʂ�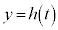 �Ƃ���Ƃ��A�ȉ��̖�ɓ�����B
�Ƃ���Ƃ��A�ȉ��̖�ɓ�����B
(1) ���ʂ����̑����ŏ㏸����Ƃ��A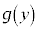 �͒萔���ł��邱�Ƃ������B
�͒萔���ł��邱�Ƃ������B (2) 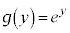 �̂Ƃ��A
�̂Ƃ��A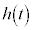 �����߂�B
�����߂�B
�y�L���z��������L���ł��B�����̊F���܂̂��x�������������肽���A��낵�����肢�������܂��B
�y�L���z�L���͂����܂łł��B
���@�e��ɐ����������ł��B�����A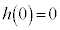 (�ŏ��ɐ��͂��܂��ĂȂ�)�Ƃ��Čv�Z��i�߂đ��v���Ǝv���܂����A�������ł͎����ēɊm�F���������ǂ��Ǝv���܂��B
(�ŏ��ɐ��͂��܂��ĂȂ�)�Ƃ��Čv�Z��i�߂đ��v���Ǝv���܂����A�������ł͎����ēɊm�F���������ǂ��Ǝv���܂��B
(1) y���̉��̉�]�̂Ȃ̂�y���ɐ����ɐ����f�ʂ͔��ax�̉~�ł��B�f�ʂ̉~�̖ʐς́A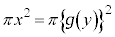 �Cy���̂܂��̉�]�̂�
�Cy���̂܂��̉�]�̂�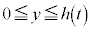 �̕������̐�(���̓����Ă��镔���̑̐�)�́At�b�Ԃɒ����ꂽ����
�̕������̐�(���̓����Ă��镔���̑̐�)�́At�b�Ԃɒ����ꂽ����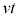 �ɓ������A
�ɓ������A 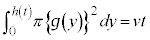 ����@
����@���ʂ���葬���ŏ㏸����Ƃ�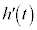 �͒萔�ŁA
�͒萔�ŁA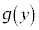 �͒萔���ł��B
�͒萔���ł��B
(2) �@��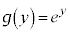 �Ƃ��āA
�Ƃ��āA
�y�L���z��������L���ł��B�����̊F���܂̂��x�������������肽���A��낵�����肢�������܂��B
�y�L���z�L���͂����܂łł��B
�@�@���嗝�H���wTOP�@�@���wTOP�@�@TOP�y�[�W�ɖ߂�
�y�L���z��������L���ł��B�����̊F���܂̂��x�������������肽���A��낵�����肢�������܂��B
�y�L���z�L���͂����܂łł��B
�e���̒��쌠��
�o���w�ɑ����܂��B©2005-2024(�L)����� ��w�y�w�m ���������t���I���n��w�l�b�g�m��w�y�w�m(���ē���������)������́A
�܂��A������܂Ń��[����
�����肭�������B