���嗝�H���w'20�N[2]
������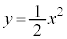 ��C�Ƃ���BC����_��P
��C�Ƃ���BC����_��P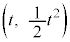 �Ƃ��Ad�𐳂̒萔�Ƃ���B�_P�ɂ�����C�ɐڂ��锼�ad�̉~�ŁA���SQ�̍��W
�Ƃ��Ad�𐳂̒萔�Ƃ���B�_P�ɂ�����C�ɐڂ��锼�ad�̉~�ŁA���SQ�̍��W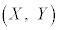 ��
��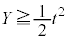 �������̂��l����B���̂Ƃ��A�ȉ��̖�ɓ�����B
�������̂��l����B���̂Ƃ��A�ȉ��̖�ɓ�����B
(1) ������C��P�ɂ�����ڐ��̕����������߂�B
(2) ������C��P�ɂ�����@���̕����������߂�B
(3) ���SQ��y���WY��t��p���ĕ\���B
(4) Y�̋ɏ��l�����߂�B
�y�L���z��������L���ł��B�����̊F���܂̂��x�������������肽���A��낵�����肢�������܂��B
�y�L���z�L���͂����܂łł��B
���@(4)��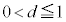 �C
�C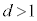 �ŏ��ς��̂ŏꍇ�������đΏ����܂��B
�ŏ��ς��̂ŏꍇ�������đΏ����܂��B
(1) C�F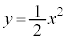 �@����@
�@����@ �������āA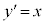 �C
�C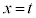 �ɂ�����ڐ��̌X����t �CP
�ɂ�����ڐ��̌X����t �CP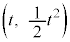 �ɂ������ڐ��̕������́A
�ɂ������ڐ��̕������́A 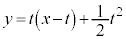 �C
�C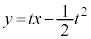 ......[��]
......[��]
(2) 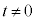 �̂Ƃ��A�@���̌X����
�̂Ƃ��A�@���̌X����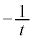 �CP�ɂ������@���̕������́A
�CP�ɂ������@���̕������́A t�������Đ�������ƁA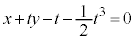 �@����A
�@����A
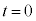 �̂Ƃ��A�@����y���ŁA
�̂Ƃ��A�@����y���ŁA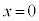 �ƂȂ�܂����A�A��
�ƂȂ�܂����A�A��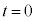 �Ƃ���ƁA
�Ƃ���ƁA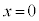 �ɂȂ�̂ŁA�A��
�ɂȂ�̂ŁA�A��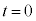 �̏ꍇ���܂�ł��܂��B����āA�@���̕������́A
�̏ꍇ���܂�ł��܂��B����āA�@���̕������́A 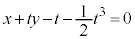 �@......[��]
�@......[��]
(3) 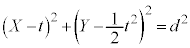 �Ƃ���(2)�̌��ʂ��g����X����������̂ł͂܂Ƃ��߂��Čv�Z����ρA�v�Z�~�X���Ăэ��݂����ł��B�Ȃ�ׂ�2�悪�o�Ă��Ȃ��悤�ɂ��邽�߂ɁA�_�ƒ����̋����̌����̗��p���l���܂��B�~�̔��a�Ɛڐ��͐����Ȃ̂ŁA�_Q
�Ƃ���(2)�̌��ʂ��g����X����������̂ł͂܂Ƃ��߂��Čv�Z����ρA�v�Z�~�X���Ăэ��݂����ł��B�Ȃ�ׂ�2�悪�o�Ă��Ȃ��悤�ɂ��邽�߂ɁA�_�ƒ����̋����̌����̗��p���l���܂��B�~�̔��a�Ɛڐ��͐����Ȃ̂ŁA�_Q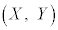 ��(2)�ŋ��߂��@����̓_�ł���A�_Q��(1)�̐ڐ��F
��(2)�ŋ��߂��@����̓_�ł���A�_Q��(1)�̐ڐ��F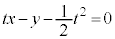 �Ƃ̋�����d�ł��B����āA
�Ƃ̋�����d�ł��B����āA 
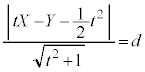 �@����B
�@����B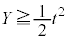 �Ȃ̂ŁA�_Q�́A�_P����㑤�A�܂�A���ɓʂȋȐ�C����㑤�ɂ���
�Ȃ̂ŁA�_Q�́A�_P����㑤�A�܂�A���ɓʂȋȐ�C����㑤�ɂ���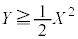 �����̂ŁA�B�̐�Βl�L�����́A
�����̂ŁA�B�̐�Βl�L�����́A�Ȃ̂ŁA�B�Ő�Βl�L�����O���ĕ�����ƁA
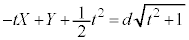 �@����C
�@����CQ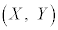 �͇A��̓_�Ȃ̂ŁA
�͇A��̓_�Ȃ̂ŁA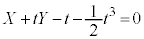 �C
�C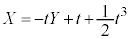
�C�ɑ�����āA
���q�̉E���̃J�b�R���͐��ł��B���q�̍����̃J�b�R���́A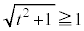 �Ȃ̂ŁA
�Ȃ̂ŁA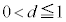 �̏ꍇ�ɂ�0�ȏ�ƂȂ�A�ꍇ�������K�v�ɂȂ�܂��B
�̏ꍇ�ɂ�0�ȏ�ƂȂ�A�ꍇ�������K�v�ɂȂ�܂��B
�E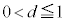 �̂Ƃ��A
�̂Ƃ��A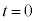 �̂Ƃ�
�̂Ƃ�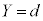 ���A�����\�́A���L�̂悤�ɂȂ�܂��B
���A�����\�́A���L�̂悤�ɂȂ�܂��B �E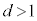 �̂Ƃ��A
�̂Ƃ��A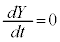 �Ƃ���ƁA
�Ƃ���ƁA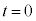 �C
�C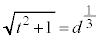 (���̂Ƃ��A
(���̂Ƃ��A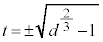 )
) 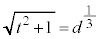 �̂Ƃ��A
�̂Ƃ��A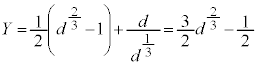 ���A�����\�́A���L�̂悤�ɂȂ�܂��B�����\���A�ɏ��l�́A
���A�����\�́A���L�̂悤�ɂȂ�܂��B�����\���A�ɏ��l�́A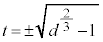 �̂Ƃ�
�̂Ƃ�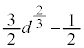
�ȏ���A�ɏ��l�́A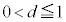 �̂Ƃ�d (
�̂Ƃ�d (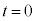 �̂Ƃ�)�C
�̂Ƃ�)�C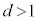 �̂Ƃ�
�̂Ƃ�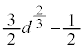 (
(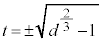 �̂Ƃ�) ......[��]
�̂Ƃ�) ......[��]
�y�L���z��������L���ł��B�����̊F���܂̂��x�������������肽���A��낵�����肢�������܂��B
�y�L���z�L���͂����܂łł��B
�@�@���嗝�H���wTOP�@�@���wTOP�@�@TOP�y�[�W�ɖ߂�
�y�L���z��������L���ł��B�����̊F���܂̂��x�������������肽���A��낵�����肢�������܂��B
�y�L���z�L���͂����܂łł��B
�e���̒��쌠��
�o���w�ɑ����܂��B©2005-2024(�L)����� ��w�y�w�m ���������t���I���n��w�l�b�g�m��w�y�w�m(���ē���������)������́A
�܂��A������܂Ń��[����
�����肭�������B 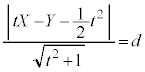 �@����B
�@����B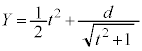 �@......[��] (
�@......[��] (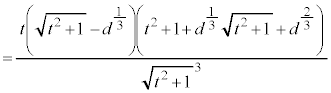
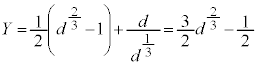 ���A�����\�́A���L�̂悤�ɂȂ�܂��B
���A�����\�́A���L�̂悤�ɂȂ�܂��B