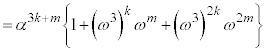���嗝�H���w'20�N[1]
���f��α�Cβ�Cγ��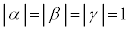 ����
����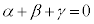 �����Ƃ��A�ȉ��̖�ɓ�����B
�����Ƃ��A�ȉ��̖�ɓ�����B
(1) α�Cβ�Cγ��\�����f���ʏ�̓_�����O�p�`���Ȃ����Ƃ������B
(2) 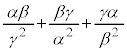 �̒l�����߂�B
�̒l�����߂�B (3) n��3�Ŋ����Ȃ����R���Ƃ���Ƃ�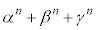 �̒l�����߂��B
�̒l�����߂��B
�y�L���z��������L���ł��B�����̊F���܂̂��x�������������肽���A��낵�����肢�������܂��B
�y�L���z�L���͂����܂łł��B
���@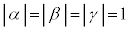 �Ƃ��������́Aα�Cβ�Cγ���\���_���P�ʉ~��ɂ��邱�Ƃ������Ă��܂��B
�Ƃ��������́Aα�Cβ�Cγ���\���_���P�ʉ~��ɂ��邱�Ƃ������Ă��܂��B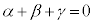 �́A3�_α�Cβ�Cγ�łł���O�p�`�̏d�S�����_�ł��邱�Ƃ������Ă��܂��B
�́A3�_α�Cβ�Cγ�łł���O�p�`�̏d�S�����_�ł��邱�Ƃ������Ă��܂��B
(1) �Ώ̐��ɂ��e�ӂ̐������������_��ʂ邱�Ƃ���A�O�p�`�̊O�S�����_�ɂȂ�܂��B�d�S�ƊO�S����v����O�p�`�͐��O�p�`�A�ƌ����܂����A�����ł́A�v�Z�ł���Ă݂܂��B 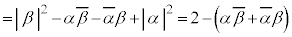 �@����@
�@����@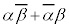 ���ǂ�������Ђ˂�o���K�v������܂����A
���ǂ�������Ђ˂�o���K�v������܂����A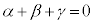 ���A
���A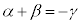 �C����āA
�C����āA�� 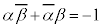 �@���A
�@���A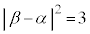
����āA3�ӂ̒������������Aα�Cβ�Cγ���\��3�_�Ő��O�p�`���Ȃ����ƂɂȂ�܂��B
(2) α�Cβ�Cγ���\��3�_���A���̏��ɔ����v���ɕ���ł���Ƃ��Ĉ�ʐ��������܂���B
(1)���A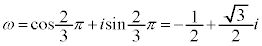 �Ƃ��āA
�Ƃ��āA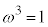 �ł����Aβ��α�����_�̉���
�ł����Aβ��α�����_�̉���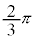 ��]�������_�Aγ��α�����_�̉���
��]�������_�Aγ��α�����_�̉���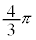 ��]�������_�ŁA
��]�������_�ŁA 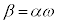 �C
�C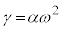
�ƕ\����܂��B
����āA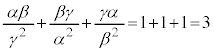 ......[��]
......[��]
(3) n��3�Ŋ����Ȃ����R���ł��邱�Ƃ���A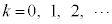 �C
�C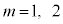 �Ƃ��āA
�Ƃ��āA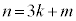 �Ƃ����ƁA
�Ƃ����ƁA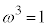 ���A
���A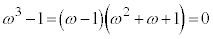 �C
�C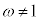 ���A
���A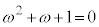 �Ȃ̂�(1�̗ݏ捪���Q��)�A
�Ȃ̂�(1�̗ݏ捪���Q��)�A 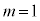 �̂Ƃ��A
�̂Ƃ��A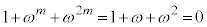
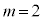 �̂Ƃ��A
�̂Ƃ��A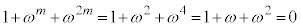
����āA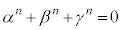 ......[��]
......[��]
�y�L���z��������L���ł��B�����̊F���܂̂��x�������������肽���A��낵�����肢�������܂��B
�y�L���z�L���͂����܂łł��B
�@�@���嗝�H���wTOP�@�@���wTOP�@�@TOP�y�[�W�ɖ߂�
�y�L���z��������L���ł��B�����̊F���܂̂��x�������������肽���A��낵�����肢�������܂��B
�y�L���z�L���͂����܂łł��B
�e���̒��쌠��
�o���w�ɑ����܂��B©2005-2024(�L)����� ��w�y�w�m ���������t���I���n��w�l�b�g�m��w�y�w�m(���ē���������)������́A
�܂��A������܂Ń��[����
�����肭�������B 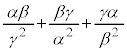 �̒l�����߂�B
�̒l�����߂�B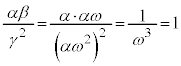 �C
�C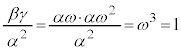 �C
�C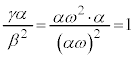
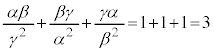 ......[��]
......[��]