早稲田大学基幹・創造・先進理工学部2021年数学入試問題
【広告】ここから広告です。ご覧の皆さまのご支援ご理解を賜りたく、よろしくお願いいたします。
【広告】広告はここまでです。
[1] xy平面上の曲線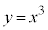
をCとする。C上の2点A
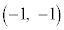，B
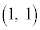をとる。さらに、C上で原点OとBの間に動点P
(
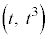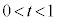)をとる。このとき、以下の問に答えよ。
(1) 直線APとx軸のなす角をαとし、直線PBとx軸のなす角をβとするとき、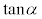
，
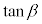をtを用いて表せ。ただし、
，
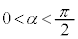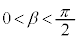とする。 (2)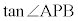 
をtを用いて表せ。 (3) 
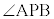を最小にするtの値を求めよ。 [解答へ]
[2] 整式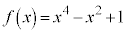
について、以下の問に答えよ。
(1) 
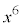を
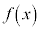で割ったときの余りを求めよ。 (2) 
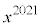を
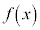で割ったときの余りを求めよ。 (3) 自然数nが3の倍数であるとき、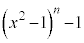
が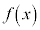
で割り切れることを示せ。 [解答へ]
[3] 複素数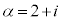
，
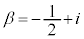に対応する複素数平面上の点を
，
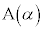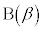とする。このとき、以下の問に答えよ。
(1) 複素数平面上の点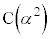
，
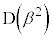と原点Oの3点は一直線上にあることを示せ。 (2) 点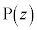
が直線AB上を動くとき、
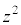の実部をx，虚部をyとして、点
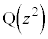の軌跡をx，yの方程式で表せ。 (3) 点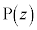
が三角形OABの周および内部にあるとき、点
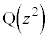全体のなす図形をKとする。Kを複素数平面上に図示せよ。 (4) (3)の図形Kの面積を求めよ。
[解答へ]
[4] n，kを2以上の自然数とする。n個の箱の中にk個の玉を無作為に入れ、各箱に入った玉の個数を数える。その最大値と最小値の差が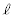
となる確率を
(
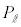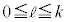)とする。このとき、以下の問に答えよ。
[解答へ]
[5] 正四面体OABCに対し、三角形ABCの外心をMとし、Mを中心として点A，B，Cを通る球面をSとする。また、Sと辺OA，OB，OCとの交点のうち、A，B，Cとは異なるものをそれぞれD，E，Fとする。さらに、Sと三角形OABの共通部分として得られる弧DEを考え、その弧を含む円周の中心をGとする。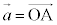
，
，
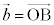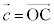として、以下の問に答えよ。
(2) 三角形OABの面積を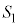
，四角形ODGEの面積を
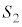とするとき、
：
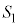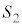をできるだけ簡単な整数により表せ。 [解答へ]
【広告】ここから広告です。ご覧の皆さまのご支援ご理解を賜りたく、よろしくお願いいたします。
【広告】広告はここまでです。
早大理工数学TOP 数学TOP TOPページに戻る
【広告】ここから広告です。ご覧の皆さまのご支援ご理解を賜りたく、よろしくお願いいたします。
【広告】広告はここまでです。
各問題の著作権は
出題大学に属します。©2005-2024(有)りるらる 苦学楽学塾 随時入会受付中！理系大学受験ネット塾苦学楽学塾(ご案内はこちら)ご入会は、
まず、こちらまでメールを
お送りください。 
，
のとき、
を求めよ。
，
のとき、
を求めよ。
，
のとき、
を求めよ。
，
，
，
を
，
，
を用いて表せ。