早稲田大学基幹・創造・先進理工学部2024年数学入試問題
【広告】ここから広告です。ご覧の皆さまのご支援ご理解を賜りたく、よろしくお願いいたします。
【広告】広告はここまでです。
[1] 円C: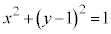 に接する直線で、x切片、y切片がともに正であるものを
に接する直線で、x切片、y切片がともに正であるものを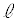 とする。Cと
とする。Cと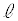 とx軸により囲まれた部分の面積をS,Cと
とx軸により囲まれた部分の面積をS,Cと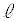 とy軸により囲まれた部分の面積をTとする。
とy軸により囲まれた部分の面積をTとする。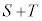 が最小となるとき、
が最小となるとき、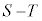 の値を求めよ。
の値を求めよ。
[解答へ]
[2] nを自然数とし、数1,2,4を重複を許してn個並べてできるn桁の自然数全体を考える。そのうちで3の倍数となるものの個数を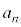 ,3で割ると1余るものの個数を
,3で割ると1余るものの個数を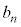 ,3で割ると2余るものの個数を
,3で割ると2余るものの個数を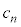 とする。
とする。
(1) 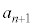 を
を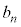 ,
,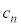 を用いて表せ。同様に、
を用いて表せ。同様に、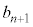 を
を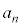 ,
,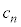 を用いて、
を用いて、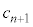 を
を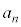 ,
,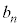 を用いて表せ。
を用いて表せ。 (2) 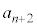 をnと
をnと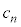 を用いて表せ。
を用いて表せ。 (3) 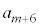 をnと
をnと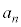 を用いて表せ。
を用いて表せ。 (4) 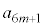 (
(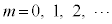 )をmを用いて表せ。
)をmを用いて表せ。 [解答へ]
[3] 点O,A,B,Cを頂点とする四面体OABCを考える。辺OA,OB,OCの中点をそれぞれP,Q,Rとし、辺BC,CA,ABの中点をそれぞれS,T,Uとする。
(1) 辺PS,QT,RUが1点で交わることを示せ。
(2) 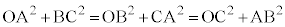 のとき、点P,Q,R,S,T,Uが同一球面上にあることを示せ。
のとき、点P,Q,R,S,T,Uが同一球面上にあることを示せ。 (3) (2)において、辺PSが辺OA,BCと直交するとし、辺OA,BCの長さをそれぞれa,kとする。点P,Q,R,S,T,Uを頂点とする八面体の体積Vをaとkを用いて表せ。
(4) (3)において、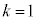 のとき八面体の体積Vの最大値を求めよ。
のとき八面体の体積Vの最大値を求めよ。 [解答へ]
[4] 2つのチームW,Kがn回試合を行う。ただし、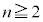 とする。各試合でのW,Kそれぞれの勝つ確率は
とする。各試合でのW,Kそれぞれの勝つ確率は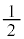 とし、引き分けはないものとする。Wが連敗しない確率を
とし、引き分けはないものとする。Wが連敗しない確率を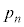 とする。ただし、連敗とは2回以上続けて負けることを言う。
とする。ただし、連敗とは2回以上続けて負けることを言う。
(1) 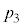 を求めよ。
を求めよ。 (3) 以下の2式を満たすα,βを求めよ。
(4) 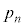 を求めよ。
を求めよ。 [解答へ]
[5] xy平面上において、以下の媒介変数表示をもつ曲線をCとする。
ただし、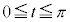 とする。
とする。
(1) yの最大値、最小値を求めよ。
(2) 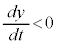 となるt の範囲を求め、Cの概形をxy平面上に描け。
となるt の範囲を求め、Cの概形をxy平面上に描け。 (3) Cをy軸のまわりに1回転してできる立体の体積Vを求めよ。
[解答へ]
【広告】ここから広告です。ご覧の皆さまのご支援ご理解を賜りたく、よろしくお願いいたします。
【広告】広告はここまでです。
早大理工数学TOP 数学TOP TOPページに戻る
【広告】ここから広告です。ご覧の皆さまのご支援ご理解を賜りたく、よろしくお願いいたします。
【広告】広告はここまでです。
各問題の著作権は
出題大学に属します。©2005-2024(有)りるらる 苦学楽学塾 随時入会受付中!理系大学受験ネット塾苦学楽学塾(ご案内はこちら)ご入会は、
まず、こちらまでメールを
お送りください。