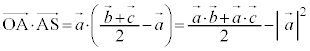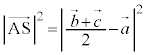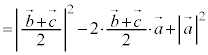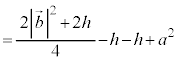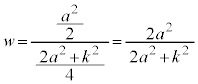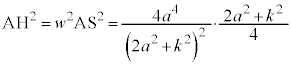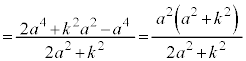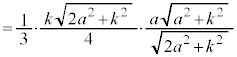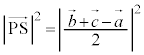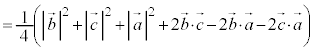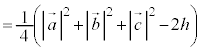���嗝�H���w'24�N[3]
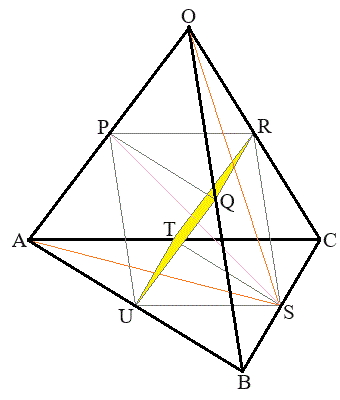
�_O�CA�CB�CC�_�Ƃ���l�ʑ�OABC���l����B��OA�COB�COC�̒��_�����ꂼ��P�CQ�CR�Ƃ��A��BC�CCA�CAB�̒��_�����ꂼ��S�CT�CU�Ƃ���B
(1) ��PS�CQT�CRU��1�_�Ō���邱�Ƃ������B
(2) 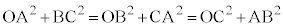 �̂Ƃ��A�_P�CQ�CR�CS�CT�CU�����ꋅ�ʏ�ɂ��邱�Ƃ������B
�̂Ƃ��A�_P�CQ�CR�CS�CT�CU�����ꋅ�ʏ�ɂ��邱�Ƃ������B (3) (2)�ɂ����āA��PS����OA�CBC�ƒ�������Ƃ��A��OA�CBC�̒��������ꂼ��a�Ck�Ƃ���B�_P�CQ�CR�CS�CT�CU�_�Ƃ��锪�ʑ̂̑̐�V��a��k��p���ĕ\���B
(4) (3)�ɂ����āA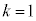 �̂Ƃ����ʑ̂̑̐�V�̍ő�l�����߂�B
�̂Ƃ����ʑ̂̑̐�V�̍ő�l�����߂�B
�y�L���z��������L���ł��B�����̊F���܂̂��x�������������肽���A��낵�����肢�������܂��B
�y�L���z�L���͂����܂łł��B
���@�����Ɏl�ʑ̂̑̐ς��l����ƁA�ȉ��̂悤�ɁA���Ȃ��ςł�(�������ԓ��ɉł���Ƃ͎v���܂���)�B�u��PS����OA�CBC�ƒ�������v�Ƃ�����蕶�̏������������Ċȕւɉ\�ł��B(4)�́A���̕s���̂��߉s�\�A�Ƃ̂��Ƃł��B
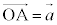 �C
�C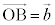 �C
�C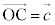 �Ƃ����ƁA
�Ƃ����ƁA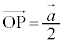 �C
�C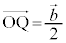 �C
�C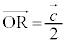 �C
�C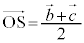 �C
�C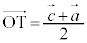 �C
�C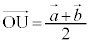 �C
�C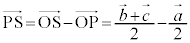 �C
�C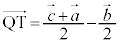 �C
�C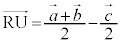 �@(�x�N�g���̓����E�O�����Q��)�@���(��)
�@(�x�N�g���̓����E�O�����Q��)�@���(��)
(1) ����PS��̓_�̈ʒu�x�N�g���́A(��)��p����(��ԃx�N�g�����Q��)�A 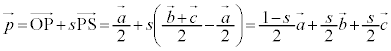 �@����@
�@����@����QT��̓_�̈ʒu�x�N�g���́A(��)��p���āA
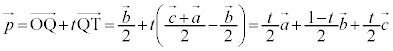 �@����A
�@����A����RU��̓_�̈ʒu�x�N�g���́A(��)��p���āA
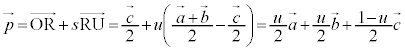 �@����B
�@����B�@�C�A�C�B�̌W�������Ƃ���ƁA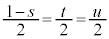 �C
�C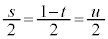 �C
�C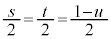 �ƂȂ�A
�ƂȂ�A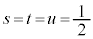 �̂Ƃ��ɖ�������܂��B���̂Ƃ��A�@�ł��A�ł��B�ł��A
�̂Ƃ��ɖ�������܂��B���̂Ƃ��A�@�ł��A�ł��B�ł��A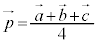 �ƂȂ�܂����A�_G��
�ƂȂ�܂����A�_G��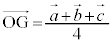 �����_�Ƃ���ƁAG�́A��PS�̒��_(
�����_�Ƃ���ƁAG�́A��PS�̒��_(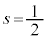 )�ł���A��QT�̒��_(
)�ł���A��QT�̒��_(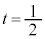 )�ł���A��RU�̒��_(
)�ł���A��RU�̒��_(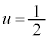 )�ł��B�@���(����)�����A��PS�CQT�CRU��1�_G�Ō����܂��B
)�ł��B�@���(����)�����A��PS�CQT�CRU��1�_G�Ō����܂��B
����āA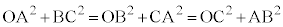 �̂Ƃ��A
�̂Ƃ��A 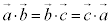 (
(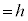 �Ƃ����܂�)�@����C
�Ƃ����܂�)�@����C�ƂȂ�܂��B�����ŁA�C��(��)��p���āA
����āA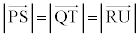 �ł��B(1)��(����)���AG�́A��PS�C��QT�C��RU�̒��_�Ȃ̂ŁA
�ł��B(1)��(����)���AG�́A��PS�C��QT�C��RU�̒��_�Ȃ̂ŁA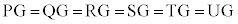 ���A�_P�CQ�CR�CS�CT�CU��G�𒆐S�Ƃ��铯�ꋅ�ʏ�ɂ���܂��B
���A�_P�CQ�CR�CS�CT�CU��G�𒆐S�Ƃ��铯�ꋅ�ʏ�ɂ���܂��B
(3) 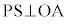 ���A�C��(��)��p���āA
���A�C��(��)��p���āA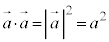 ���A
���A
�� 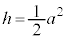 �@����D
�@����D
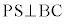 ���A�C��p���āA
���A�C��p���āA �� 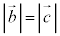 �@����E
�@����E
�܂��A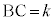 ���A�C�C�D�C�E��p���āA
���A�C�C�D�C�E��p���āA �� 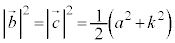 �@����F
�@����F
�C�C�D�C�F��p���āA 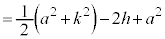
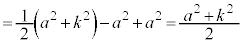 �@����G
�@����G���l�ɁA�F���A
��ABC�́AAB = AC�̓ӎO�p�`�ŁA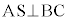 �C
�C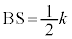 �C�G���A
�C�G���A 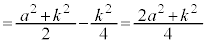 �@����H
�@����H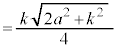 �@����I
�@����IO���灢ABC�ɐ����������ƁA�����̑�H�́AAS��ɗ��܂��B
w�������Ƃ��āA(��)��p���āA
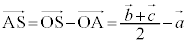 �@����J
�@����J
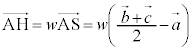 �@����K
�@����K�Ƃ����ƁA
�ł����āA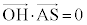 ���A
���A 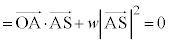 �@����L
�@����L�J�C�C�C�D��p���āA
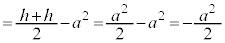 �@����M
�@����M�C�C�D�C�F�C�J���A
�M�C�N���L�ɑ�����邱�Ƃɂ��A
�K�C�N���A
����ƇI���A�l�ʑ�OABC���̐�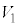 �́A
�́A 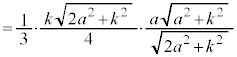
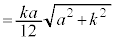 �@����O
�@����O�Ƃ���ŁA�_P�CQ�CR�CS�CT�CU�_�Ƃ��锪�ʑ̂́A�l�ʑ�OABC����l�ʑ�OPQR�C�l�ʑ�APQU�C�l�ʑ�BSQU�C�l�ʑ�CRST����菜�������̂ł��B�_P�CQ�CR�CS�CT�CU���l�ʑ�OABC�̊e�ӂ̒��_�ł��邱�Ƃ���A�l�ʑ�OPQR�C�l�ʑ�APQU�C�l�ʑ�BSQU�C�l�ʑ�CRST�̑̐ς́A�l�ʑ�OABC�̑̐�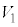 ��
��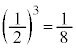 �ł�(�ʐϔ�E�̐ϔ����Q��)�B�O���A���ʑ̂̑̐�V�́A
�ł�(�ʐϔ�E�̐ϔ����Q��)�B�O���A���ʑ̂̑̐�V�́A 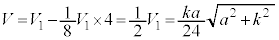 ......[��]
......[��]
�ʉ��D��L�ł́A��ABC���ʂƍl�������߂ɍ��������߂�̂ɋ�J���邱�ƂɂȂ�܂������A���X�H�v���邱�Ƃɂ��A���̍�Ƃ�������邱�Ƃ��ł��܂��B
[��@1]�@��蕶��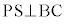 ���������āA�l�ʑ�OABC����OAS�Ő��āA�l�ʑ�COAS�Ǝl�ʑ�BOAS�ɕ����܂��BS��BC�̒��_�ł���A(2)���AB=AC�C�F���OB=OC�C����āA����2�̎l�ʑ͍̂����ŁA�l�ʑ�BOAS�́A��OAS���ʂƍl����ƍ�����
���������āA�l�ʑ�OABC����OAS�Ő��āA�l�ʑ�COAS�Ǝl�ʑ�BOAS�ɕ����܂��BS��BC�̒��_�ł���A(2)���AB=AC�C�F���OB=OC�C����āA����2�̎l�ʑ͍̂����ŁA�l�ʑ�BOAS�́A��OAS���ʂƍl����ƍ�����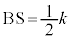 �ł��B
�ł��B ��L�C�C�D�C�F���A
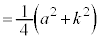 �@����P
�@����P�l�ʑ�BOAS�̑̐ς́A
�l�ʑ�OABC�̑̐ς͂���2�{�ŁA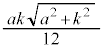
���ʑ̂̑̐ς́A����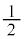 �ŁA
�ŁA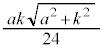
[��@2]�@�_P�CQ�CR�CS�CT�CU�_�Ƃ��锪�ʑ̂��l�p�`QRTU(�E��}���F���F��)�Ő���2�ɕ����A�l�p��PQRTU�Ǝl�p��SQRTU�ɕ����܂��B�ȉ��Ō���悤�ɒ��_�A���藝���A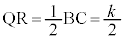 �C
�C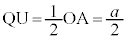 �C
�C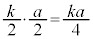 �C
�C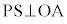 �C����āA����2�̎l�p���͍����ł��B��COA�ɂ����āA���_�A���藝���AOA // RT
�C����āA����2�̎l�p���͍����ł��B��COA�ɂ����āA���_�A���藝���AOA // RT ��BOA�ɂ����āA���_�A���藝���AOA // QU����āART // QU���l�ɁAQR // UT�܂��A��L(2)���AQT = RU�ł����āA�l�p�`QRTU�͒����`�ŁA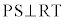 �C
�C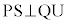 ���A���̖ʐς́A
���A���̖ʐς́A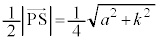 �ł��B
�ł��B
�܂�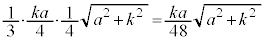 ���A
���A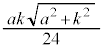 �C
�C �C����āAPS�͒����`QRTU�Ɛ����ł��B
�C����āAPS�͒����`QRTU�Ɛ����ł��B
�P���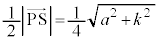 �Ȃ̂ŁA�l�p��PQRTU�̑̐ς́A
�Ȃ̂ŁA�l�p��PQRTU�̑̐ς́A �ł��B���ʑ̂̑̐ς́A����2�{�ŁA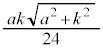
�y�L���z��������L���ł��B�����̊F���܂̂��x�������������肽���A��낵�����肢�������܂��B
�y�L���z�L���͂����܂łł��B
�@�@���嗝�H���wTOP�@�@���wTOP�@�@TOP�y�[�W�ɖ߂�
�y�L���z��������L���ł��B�����̊F���܂̂��x�������������肽���A��낵�����肢�������܂��B
�y�L���z�L���͂����܂łł��B
�e���̒��쌠��
�o���w�ɑ����܂��B©2005-2024(�L)����� ��w�y�w�m ���������t���I���n��w�l�b�g�m��w�y�w�m(���ē���������)������́A
�܂��A������܂Ń��[����
�����肭�������B 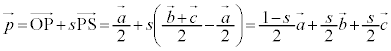 �@����@
�@����@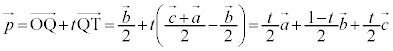 �@����A
�@����A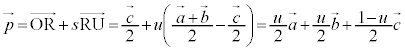 �@����B
�@����B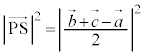
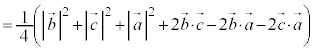
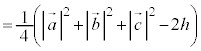
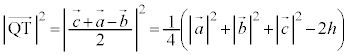
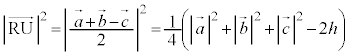
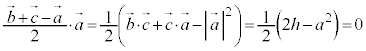
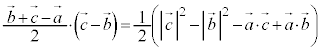
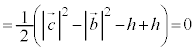
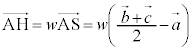 �@����K
�@����K