���嗝�H���w'24�N[4]
2�̃`�[��W�CK��n�����s���B�������A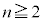 �Ƃ���B�e�����ł�W�CK���ꂼ��̏��m����
�Ƃ���B�e�����ł�W�CK���ꂼ��̏��m����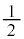 �Ƃ��A���������͂Ȃ����̂Ƃ���BW���A�s���Ȃ��m����
�Ƃ��A���������͂Ȃ����̂Ƃ���BW���A�s���Ȃ��m����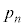 �Ƃ���B�������A�A�s�Ƃ�2��ȏ㑱���ĕ����邱�Ƃ������B
�Ƃ���B�������A�A�s�Ƃ�2��ȏ㑱���ĕ����邱�Ƃ������B
(1) 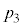 �����߂�B
�����߂�B (3) �ȉ���2������α�Cβ�����߂�B�������A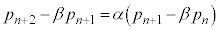 �Ƃ���B
�Ƃ���B (4) 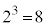 �����߂�B
�����߂�B
�y�L���z��������L���ł��B�����̊F���܂̂��x�������������肽���A��낵�����肢�������܂��B
�y�L���z�L���͂����܂łł��B
���@W������c��K���c��ł��傤���H�����ɂ����c��̂悤�ȕ��͋C�̖��ŁA�u�A�s�v�Ƃ͉������I�Ɩ싅���ɓ{��ꂽ�肵�Ȃ��̂ł��傤���H
(1) �������Z�A���������ŕ\���ƁA3�������ĘA�s���Ȃ��̂́A
�Z�Z�Z�C�Z�Z���C�Z���Z�C���Z�Z�C���Z����5�ʂ肠��܂��B3�����ł̏��s�̃p�^�[����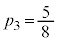 �ʂ肠��܂��B���߂��m���́A
�ʂ肠��܂��B���߂��m���́A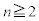 ......[��]��蕶�ł�
......[��]��蕶�ł�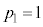 �ƂȂ��Ă��܂����A1�����̏ꍇ���l���ɓ����ƁA1�����ł͘A�s�Ƃ������Ƃ͂Ȃ��̂ŁA
�ƂȂ��Ă��܂����A1�����̏ꍇ���l���ɓ����ƁA1�����ł͘A�s�Ƃ������Ƃ͂Ȃ��̂ŁA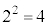 �ł��B2�����ŘA�s����̂́A������1�ʂ�A2�����̏��s�̃p�^�[����
�ł��B2�����ŘA�s����̂́A������1�ʂ�A2�����̏��s�̃p�^�[����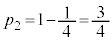 �ʂ�A
�ʂ�A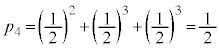
���s�ǂ���ł��悢�A�Ƃ����̂��~�ŕ\���āA4�������ƁA�A�s�́A�����~�~�C�Z�����~�C�~�Z�����̏ꍇ�ŁA���ꂼ��̊m�����������킹�āA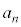
(2) n�����ڂɘA�s���Ă��Ȃ��A�ƌ����Ă��An�����ڂɏ����ĘA�s���Ȃ��ꍇ�ƁA�����ĘA�s���Ȃ��ꍇ�������Q�����𗧂Ăɂ������Ȃ̂ŁA��2�ɕ����āAn�����ڂɏ����ĘA�s���Ă��Ȃ��m����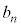 �Cn�����ڂɕ����ĘA�s���Ă��Ȃ��m����
�Cn�����ڂɕ����ĘA�s���Ă��Ȃ��m����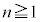 �Ƃ��܂��B
�Ƃ��܂��B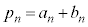 �Ƃ��Ă����܂��B���Ҕr���ŁA
�Ƃ��Ă����܂��B���Ҕr���ŁA 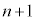 �@����@
�@����@�ł��Bn�����ڂɏ����ĘA�s���Ă��Ȃ��ꍇ�́A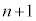 �����ڂ̌��ʂɂ�����炸�A
�����ڂ̌��ʂɂ�����炸�A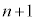 �����ڂ܂ŘA�s���Ă��܂���B
�����ڂ܂ŘA�s���Ă��܂���B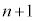 �����ڂɏ����ĘA�s���Ă��Ȃ��m����
�����ڂɏ����ĘA�s���Ă��Ȃ��m����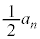 �����ڂɕ����ĘA�s���Ă��Ȃ��m�����Ƃ���
�����ڂɕ����ĘA�s���Ă��Ȃ��m�����Ƃ���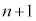 �ł��Bn�����ڂɕ����ĘA�s���Ă��Ȃ��ꍇ�́A
�ł��Bn�����ڂɕ����ĘA�s���Ă��Ȃ��ꍇ�́A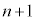 �����ڂɏ������ꍇ�̂݁A
�����ڂɏ������ꍇ�̂݁A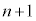 �����ڂ܂łŘA�s���܂���B���̊m��(
�����ڂ܂łŘA�s���܂���B���̊m��(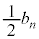 �����ڂɏ����ĘA�s���Ă��Ȃ�)��
�����ڂɏ����ĘA�s���Ă��Ȃ�)��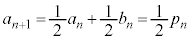 �ł��B
�ł��B
�ȏ���A�@���l�����āA 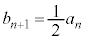 �@����A
�@����A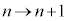
�܂��A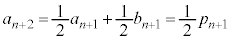 �Ƃ��āA
�Ƃ��āA 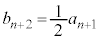 �@����B
�@����B
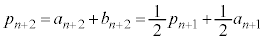 �@����C
�@����C�A�C�B�C�C��p���āA
�� 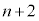 ......[��]�@����D
......[��]�@����D
��������đQ�������ł��Ă݂�ƁA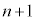 �����ڂ܂ŘA�s���Ȃ��̂́A
�����ڂ܂ŘA�s���Ȃ��̂́A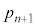 �����ڂ܂ŘA�s����(�m��
�����ڂ܂ŘA�s����(�m��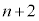 )��
)��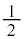 �����ڂɏ���(�m��
�����ڂɏ���(�m��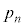 )���An�����ڂ܂ŘA�s����(�m��
)���An�����ڂ܂ŘA�s����(�m��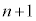 )�ɁA
)�ɁA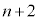 �����ڂɏ�����
�����ڂɏ�����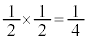 �����ڂɕ�����(�m��
�����ڂɕ�����(�m��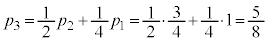 )�Ƃ����A�Ƃ������Ƃ�������܂��B
)�Ƃ����A�Ƃ������Ƃ�������܂��B
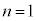 ��
��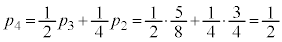 �̂Ƃ��A�Q���������Ă��܂��B
�̂Ƃ��A�Q���������Ă��܂��B
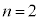 ��
��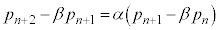 �̂Ƃ��A�Q���������Ă��܂��B
�̂Ƃ��A�Q���������Ă��܂��B
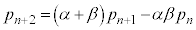 �@����F
�@����F���������Ă���Ƃ��āA
��2���ŁA
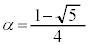 ���A
���A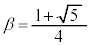 �C
�C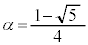 �Ƃ��āA�E�C�F�������܂��B
�Ƃ��āA�E�C�F�������܂��B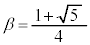 �C
�C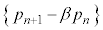 ......[��]
......[��]
(4) �E���A����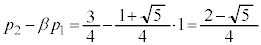 �́A����Fα�C�����F
�́A����Fα�C�����F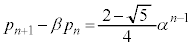 �����䐔���ł��B����āA
�����䐔���ł��B����āA 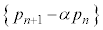 �@����G
�@����G�F���A����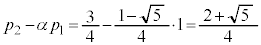 �́A����Fβ�C�����F
�́A����Fβ�C�����F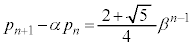 �̓��䐔��ł��B����āA
�̓��䐔��ł��B����āA 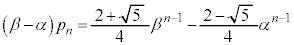 �@����H
�@����H�H�|�G���A
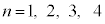 ......[��]
......[��]
�y�L���z��������L���ł��B�����̊F���܂̂��x�������������肽���A��낵�����肢�������܂��B
�y�L���z�L���͂����܂łł��B
�@�@���嗝�H���wTOP�@�@���wTOP�@�@TOP�y�[�W�ɖ߂�
�y�L���z��������L���ł��B�����̊F���܂̂��x�������������肽���A��낵�����肢�������܂��B
�y�L���z�L���͂����܂łł��B
�e���̒��쌠��
�o���w�ɑ����܂��B©2005-2024(�L)����� ��w�y�w�m ���������t���I���n��w�l�b�g�m��w�y�w�m(���ē���������)������́A
�܂��A������܂Ń��[����
�����肭�������B 
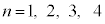 ......[��]
......[��]