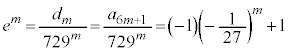���嗝�H���w'24�N[2]
n�����R���Ƃ��A��1�C2�C4���d����������n���ׂĂł���n���̎��R���S�̂��l����B���̂�����3�̔{���ƂȂ���̂̌���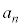 �C3�Ŋ����1�]����̂̌���
�C3�Ŋ����1�]����̂̌���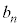 �C3�Ŋ����2�]����̂̌���
�C3�Ŋ����2�]����̂̌���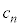 �Ƃ���B
�Ƃ���B
(1) 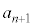 ��
��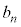 �C
�C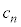 ��p���ĕ\���B���l�ɁA
��p���ĕ\���B���l�ɁA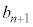 ��
��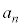 �C
�C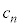 ��p���āA
��p���āA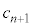 ��
��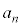 �C
�C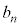 ��p���ĕ\���B
��p���ĕ\���B (2) 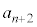 ��n��
��n��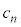 ��p���ĕ\���B
��p���ĕ\���B (3) 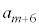 ��n��
��n��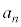 ��p���ĕ\���B
��p���ĕ\���B (4) 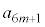 (
(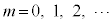 )��m��p���ĕ\���B
)��m��p���ĕ\���B
�y�L���z��������L���ł��B�����̊F���܂̂��x�������������肽���A��낵�����肢�������܂��B
�y�L���z�L���͂����܂łł��B
���@���R����10�i�@�ŕ\���Ƃ��A�e���̐����̘a��3�Ŋ�������̎��R����3�̔{���ł���A�e���̐����̘a��3�Ŋ�����1�]����̎��R����3�Ŋ����1�]��A�e���̐����̘a��3�Ŋ�����2�]����̎��R����3�Ŋ����2�]��A�Ƃ�������(�������Q��)���g���čl���܂��A����킯�ł͂Ȃ��̂ŁA�o�ꂷ�鐔���傫���Ă��f�킳��Ȃ��悤�ɂ��܂��傤�B
(1) 3�Ŋ�����n���̎��R��(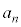 ��)��
��)��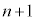 ���߂�1�C4��t������ƁA3�Ŋ����1�]��
���߂�1�C4��t������ƁA3�Ŋ����1�]��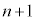 ���̎��R����
���̎��R����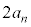 �ł��܂��B
�ł��܂��B 3�Ŋ�����n���̎��R��(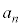 ��)��
��)��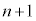 ���߂�2��t������ƁA3�Ŋ����2�]��
���߂�2��t������ƁA3�Ŋ����2�]��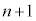 ���̎��R����
���̎��R����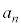 �ł��܂��B3�Ŋ����1�]��n���̎��R��(
�ł��܂��B3�Ŋ����1�]��n���̎��R��(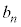 ��)��
��)��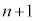 ���߂�1�C4��t������ƁA3�Ŋ����2�]��
���߂�1�C4��t������ƁA3�Ŋ����2�]��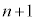 ���̎��R����
���̎��R����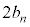 �ł��܂��B3�Ŋ����1�]��n���̎��R��(
�ł��܂��B3�Ŋ����1�]��n���̎��R��(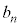 ��)��
��)��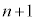 ���߂�2��t������ƁA3�Ŋ��肫���
���߂�2��t������ƁA3�Ŋ��肫���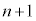 ���̎��R����
���̎��R����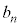 �ł��܂��B3�Ŋ����2�]��n���̎��R��(
�ł��܂��B3�Ŋ����2�]��n���̎��R��(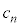 ��)��
��)��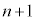 ���߂�1�C4��t������ƁA3�Ŋ��肫���
���߂�1�C4��t������ƁA3�Ŋ��肫���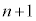 ���̎��R����
���̎��R����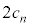 �ł��܂��B3�Ŋ����2�]��n���̎��R��(
�ł��܂��B3�Ŋ����2�]��n���̎��R��(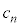 ��)��
��)��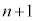 ���߂�2��t������ƁA3�Ŋ����1�]��
���߂�2��t������ƁA3�Ŋ����1�]��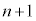 ���̎��R����
���̎��R����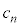 �ł��܂��B
�ł��܂��B
����āA���߂��A���Q�����́A 3����ӁX�������킹��ƁA
����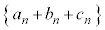 �́A����3�F����
�́A����3�F����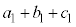 �����䐔���ł��B1���̎��R���A1�C2�C4�ŁA3�Ŋ�������̂�
�����䐔���ł��B1���̎��R���A1�C2�C4�ŁA3�Ŋ�������̂�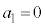 �A3�Ŋ����1�]����̂�
�A3�Ŋ����1�]����̂�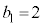 �A3�Ŋ����2�]����̂�
�A3�Ŋ����2�]����̂�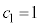 ����܂��B
����܂��B ����āA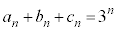 �@����@
�@����@
(2) (1)�̌���(��)��p���āA
������(��)�������āA
�@���A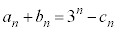 �C����������A
�C����������A 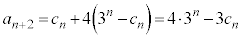 ......[��]�@����A
......[��]�@����A���l�ɂ��āA
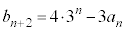 �@����B
�@����B
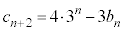 �@����C
�@����C
(3) �A���A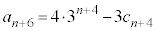
�C���A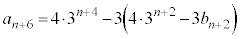
�B���A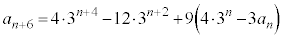
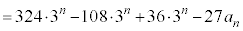
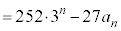 ......[��]�@����D
......[��]�@����D
(4) �D�ɂ����āA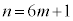 �Ƃ��āA
�Ƃ��āA 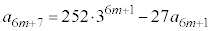 �@����E
�@����E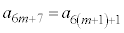 ���A
���A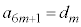 (
(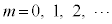 )�Ƃ�����
)�Ƃ�����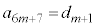 �C
�C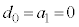 �C�܂��A
�C�܂��A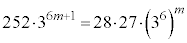 ���A�E������������ƁA
���A�E������������ƁA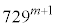 �Ŋ���ƁA
�Ŋ���ƁA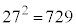 �ł����āA
�ł����āA�F�|�G���A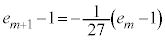
����āA����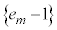 �́A����F
�́A����F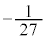 �C�����F
�C�����F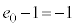 �ł��铙�䐔��B
�ł��铙�䐔��B
�� 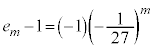
�� 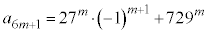 ......[��]
......[��]
�y�L���z��������L���ł��B�����̊F���܂̂��x�������������肽���A��낵�����肢�������܂��B
�y�L���z�L���͂����܂łł��B
�@�@���嗝�H���wTOP�@�@���wTOP�@�@TOP�y�[�W�ɖ߂�
�y�L���z��������L���ł��B�����̊F���܂̂��x�������������肽���A��낵�����肢�������܂��B
�y�L���z�L���͂����܂łł��B
�e���̒��쌠��
�o���w�ɑ����܂��B©2005-2024(�L)����� ��w�y�w�m ���������t���I���n��w�l�b�g�m��w�y�w�m(���ē���������)������́A
�܂��A������܂Ń��[����
�����肭�������B