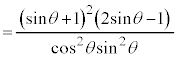早大理工数学'24年[1]
円C: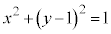 に接する直線で、x切片、y切片がともに正であるものを
に接する直線で、x切片、y切片がともに正であるものを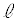 とする。Cと
とする。Cと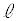 とx軸により囲まれた部分の面積をS,Cと
とx軸により囲まれた部分の面積をS,Cと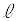 とy軸により囲まれた部分の面積をTとする。
とy軸により囲まれた部分の面積をTとする。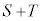 が最小となるとき、
が最小となるとき、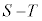 の値を求めよ。
の値を求めよ。
【広告】ここから広告です。ご覧の皆さまのご支援ご理解を賜りたく、よろしくお願いいたします。
【広告】広告はここまでです。
解答 以下では、平凡に正直に計算して解答します。
円C上の点は、円Cの半径が1 (円の方程式を参照)なので、θを実数として、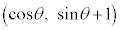 と表せます(円の媒介変数表示を参照)。
と表せます(円の媒介変数表示を参照)。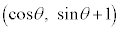 における円Cの接線
における円Cの接線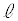 は(円の接線を参照)、
は(円の接線を参照)、
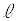 :
: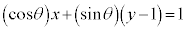
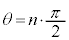 のときの接線はx軸、またはy軸に垂直な直線で、x軸と囲む面積、y軸と囲む面積を作り得ないので、
のときの接線はx軸、またはy軸に垂直な直線で、x軸と囲む面積、y軸と囲む面積を作り得ないので、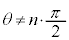 とします。
とします。
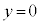 としてx切片は、
としてx切片は、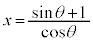
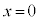 としてy切片は、
としてy切片は、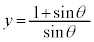
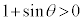 なので、x切片、y切片がともに正であることから、
なので、x切片、y切片がともに正であることから、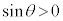 ,
,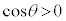
よって、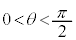 として考えれば十分です。
として考えれば十分です。
直線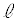 とx軸,y軸との交点をM,Nとする(x切片はMのx座標、y切片はNのy座標)と、
とx軸,y軸との交点をM,Nとする(x切片はMのx座標、y切片はNのy座標)と、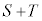 は、三角形OMNの面積から、半径1の半円の面積
は、三角形OMNの面積から、半径1の半円の面積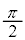 を引いたものです。よって、
を引いたものです。よって、
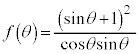 とおくと、
とおくと、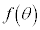 最小のときに
最小のときに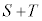 最小です。
最小です。
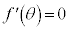 とすると、
とすると、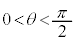 においては
においては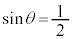 より
より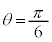 ,このとき、
,このとき、
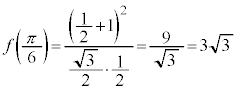 ,
,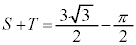 ,x切片:
,x切片: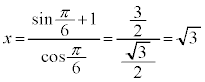 ,y切片:
,y切片: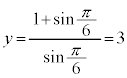 増減表は以下。
増減表は以下。
 増減表より、
増減表より、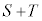 は
は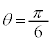 のとき最小値
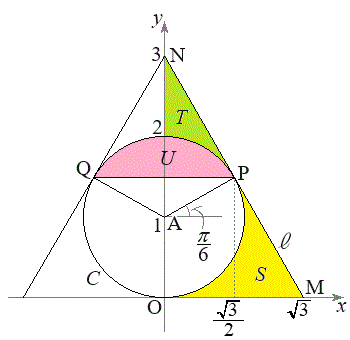
のとき最小値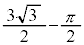 をとります。このときの状況を右図に示します。Sは黄色、Tは緑色で示しました。
をとります。このときの状況を右図に示します。Sは黄色、Tは緑色で示しました。
右図で、扇形APQから三角形APQを取り除いた部分Uをピンクで示しました。
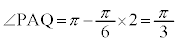 なので、扇形APQの面積は円Cの
なので、扇形APQの面積は円Cの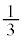 で
で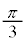 です。
です。
注.右図を見れば、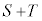 が最小、つまり
が最小、つまり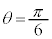 のとき、△AMP≡△ANPなので
のとき、△AMP≡△ANPなので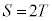 です。
です。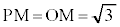 より、△OAM
より、△OAM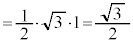 ,
,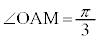 より、△OAMの面積から半径1の円の面積の
より、△OAMの面積から半径1の円の面積の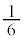 を引いて、
を引いて、 とすることもできます。
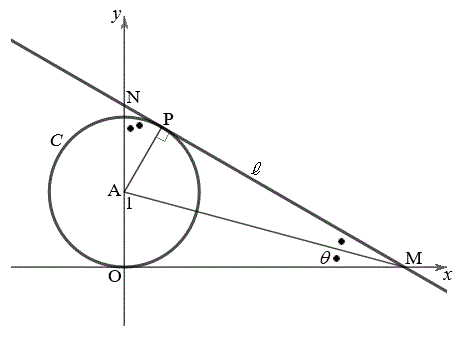 別解.上記ではあまりに真正直なので、多少工夫をしてみます。円Cの中心をA
別解.上記ではあまりに真正直なので、多少工夫をしてみます。円Cの中心をA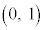 ,円Cの接線
,円Cの接線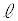 との接点をP,接線
との接点をP,接線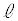 とx軸,y軸との交点をM,N,右図で
とx軸,y軸との交点をM,N,右図で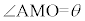 とします。
とします。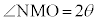 です。
です。上記にも書きましたが、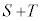 は、△OMNの面積から半円の面積
は、△OMNの面積から半円の面積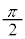 を引いたものです。右図より、
を引いたものです。右図より、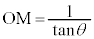 ,
,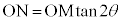 ,
,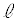 のx切片,y切片がともに正であるために
のx切片,y切片がともに正であるために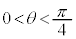 です。
です。 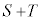 が最小のとき、△OMNの面積も最小で、このとき分母の
が最小のとき、△OMNの面積も最小で、このとき分母の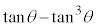 は最大です。
は最大です。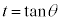 として、
として、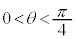 より、
より、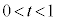 です。
です。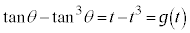 とおくと、
とおくと、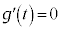 とすると、
とすると、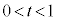 より
より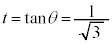 ,
,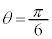 のとき
のとき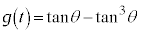 最大です。
最大です。
たまたまできた感はありますが、これで、上記注.のようにすれば、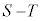 が求められます。
が求められます。
【広告】ここから広告です。ご覧の皆さまのご支援ご理解を賜りたく、よろしくお願いいたします。
【広告】広告はここまでです。
早大理工数学TOP 数学TOP TOPページに戻る
【広告】ここから広告です。ご覧の皆さまのご支援ご理解を賜りたく、よろしくお願いいたします。
【広告】広告はここまでです。
各問題の著作権は
出題大学に属します。©2005-2024(有)りるらる 苦学楽学塾 随時入会受付中!理系大学受験ネット塾苦学楽学塾(ご案内はこちら)ご入会は、
まず、こちらまでメールを
お送りください。 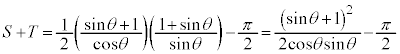
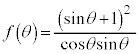 とおくと、
とおくと、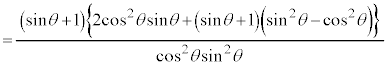
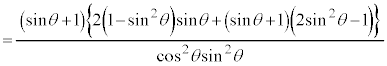
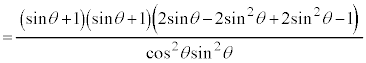 (∵
(∵