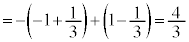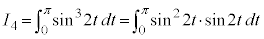���嗝�H���w'24�N[5]
xy���ʏ�ɂ����āA�ȉ��̔}��ϐ��\�������Ȑ���C�Ƃ���B
�������A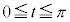 �Ƃ���B
�Ƃ���B
(1) y�̍ő�l�A�ŏ��l�����߂�B
(2) 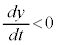 �ƂȂ�t �͈̔͂����߁AC�̊T�`��xy���ʏ�ɕ`���B
�ƂȂ�t �͈̔͂����߁AC�̊T�`��xy���ʏ�ɕ`���B (3) C��y���̂܂���1��]���Ăł��闧�̂̑̐�V�����߂�B
�y�L���z��������L���ł��B�����̊F���܂̂��x�������������肽���A��낵�����肢�������܂��B
�y�L���z�L���͂����܂łł��B
���@�Ȑ�C���J�[�W�I�C�h�ł��B(3)�̗��̂̑̐ς́A��]�����Ƃ��ɂ��蔲���镔�������邱�Ƃɒ��ӂ��܂��傤�B
x��y��t �Ŕ��������(�}��ϐ��\�����ꂽ���̔����@���Q��)�A
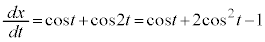
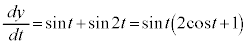
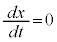 �Ƃ���ƁA
�Ƃ���ƁA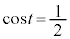 �܂���
�܂���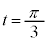 �C�����
�C�����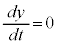
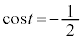 �Ƃ���ƁA
�Ƃ���ƁA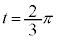 �܂���
�܂���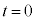 �C
�C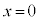
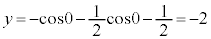 �̂Ƃ��A
�̂Ƃ��A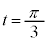 �C
�C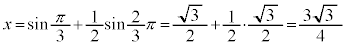
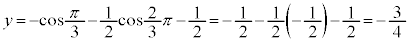 �̂Ƃ��A
�̂Ƃ��A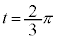 �C
�C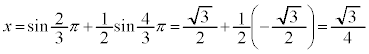
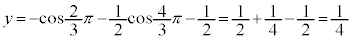 �̂Ƃ��A
�̂Ƃ��A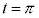 �C
�C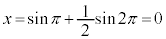
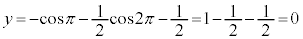 �̂Ƃ��A
�̂Ƃ��A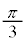 �C
�C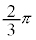
�����\�͈ȉ��̂悤�ɂȂ�܂��B
| t | 0 | �@ | 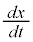 | �@ | 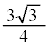 | �@ | π |
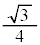 | + | �{ | 0 | �| | �| | �| | 0 |
| x | 0 |  | 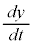 |  | 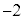 |  | 0 |
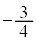 | 0 | �{ | �{ | �{ | 0 | �| | 0 |
| y | 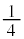 |  | 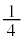 |  | 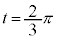 |  | 0 |
>
(1) ��L�̑����\�ɂ��Ay�̍ő�l��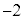 (
(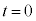 �̂Ƃ�)�C�ŏ��l��
�̂Ƃ�)�C�ŏ��l��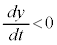 (
(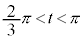 �̂Ƃ�) ......[��]
�̂Ƃ�) ......[��] 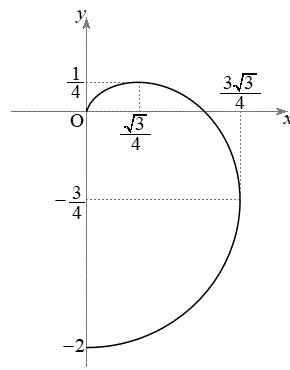
(2) ��L�̑����\���A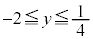 �ƂȂ�t �͈̔͂́A
�ƂȂ�t �͈̔͂́A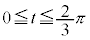 ......[��]
......[��] C�̊T�`�͉E�}�B
(3) C��y���̂܂���1��]���Ăł������̂̑̐��́A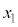 �̕���(��L�����\��
�̕���(��L�����\��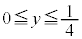 �͈̔́B���͈̔͂�x���ȉ��̐ϕ��ł�
�͈̔́B���͈̔͂�x���ȉ��̐ϕ��ł�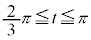 �Ƃ��܂�)����]���������̂���A
�Ƃ��܂�)����]���������̂���A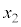 �̓���(��L�̑����\��
�̓���(��L�̑����\��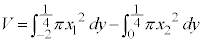 �͈̔́B���͈̔͂�x���ȉ��̐ϕ��ł�
�͈̔́B���͈̔͂�x���ȉ��̐ϕ��ł�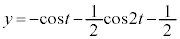 �Ƃ��܂�)����]���������̂��������̐ςɂȂ�܂��B
�Ƃ��܂�)����]���������̂��������̐ςɂȂ�܂��B �����ŁA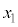 �Ƃ������u���ϕ�����ƁA
�Ƃ������u���ϕ�����ƁA
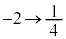 �C
�C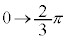 �ɑ��ẮAy�F
�ɑ��ẮAy�F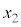 �̂Ƃ�t�F
�̂Ƃ�t�F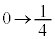 �C
�C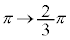 �ɑ��ẮAy�F
�ɑ��ẮAy�F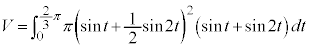 �̂Ƃ�t�F
�̂Ƃ�t�F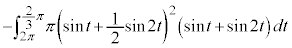
�����ŁA��ϕ����́A
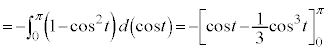 �@����@
�@����@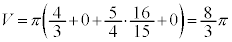 ......[��]
......[��]
�y�L���z��������L���ł��B�����̊F���܂̂��x�������������肽���A��낵�����肢�������܂��B
�y�L���z�L���͂����܂łł��B
�@�@���嗝�H���wTOP�@�@���wTOP�@�@TOP�y�[�W�ɖ߂�
�y�L���z��������L���ł��B�����̊F���܂̂��x�������������肽���A��낵�����肢�������܂��B
�y�L���z�L���͂����܂łł��B
�e���̒��쌠��
�o���w�ɑ����܂��B©2005-2024(�L)����� ��w�y�w�m ���������t���I���n��w�l�b�g�m��w�y�w�m(���ē���������)������́A
�܂��A������܂Ń��[����
�����肭�������B 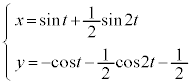
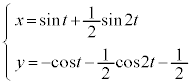
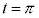 �C
�C