�A���y�[������ϕ��̖@��
�y�L���z��������L���ł��B�����̊F���܂̂��x�������������肽���A��낵�����肢�������܂��B
�y�L���z�L���͂����܂łł��B
�Ȑ�C�ň͂ޖʂ��d��I���т��Ă���Ƃ��AC��̊e�_�ɂ��������E��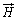 �Ƃ��āA
�Ƃ��āA
������A�A���y�[������ϕ��̖@���ƌ����B
�r�I�E�T�o�[���̖@�����A�d���̗����o�HC�ɉ��������ϕ����ē����鎮�F
�����ŁA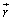 �́AC����d���f��
�́AC����d���f��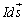 �̈ʒu����_����A���E
�̈ʒu����_����A���E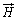 ���l���Ă���_�Ɍ������x�N�g���ł��B
���l���Ă���_�Ɍ������x�N�g���ł��B
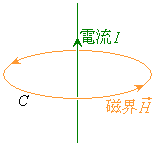
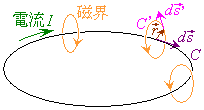 �r�I�E�T�o�[���̖@���ɂ��A�d���������ƁA�d���̗����������E�˂��̐i�ތ����Ƃ��āA�d���o�H�����͐������͂ނ悤�ɁA�E�˂��̉����������E���������܂�(���̎������u�A���y�[���E�˂��̖@���v�A�P�Ɂu�A���y�[���̖@���v�ƌĂԂ��Ƃ�����܂�)�B
�r�I�E�T�o�[���̖@���ɂ��A�d���������ƁA�d���̗����������E�˂��̐i�ތ����Ƃ��āA�d���o�H�����͐������͂ނ悤�ɁA�E�˂��̉����������E���������܂�(���̎������u�A���y�[���E�˂��̖@���v�A�P�Ɂu�A���y�[���̖@���v�ƌĂԂ��Ƃ�����܂�)�B
�@�̗��ӂ�1�{�����͐��̌o�H�ƂȂ�Ȑ�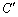 �ɉ����Đ��ϕ����Ă݂܂��BC�ɉ��������f
�ɉ����Đ��ϕ����Ă݂܂��BC�ɉ��������f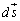 �Ƌ�ʂ��āA
�Ƌ�ʂ��āA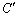 �ɉ��������f��
�ɉ��������f��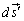 �Ƃ��܂�(���̕ӂ̋c�_�́A��g�u���E����̕����w2�u�d���͊w�v���c�O����57�y�[�W�ɂ킩��Ղ����������܂�)�B
�Ƃ��܂�(���̕ӂ̋c�_�́A��g�u���E����̕����w2�u�d���͊w�v���c�O����57�y�[�W�ɂ킩��Ղ����������܂�)�B
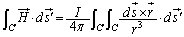 �@����A
�@����A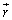 �́A
�́A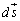 �̈ʒu����_����
�̈ʒu����_����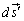 �̈ʒu����_�Ɍ������x�N�g���ł��B
�̈ʒu����_�Ɍ������x�N�g���ł��B
�x�N�g���̌����F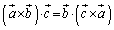 (�O�����Q��)���A
(�O�����Q��)���A
�����ŁA�Ȑ�C���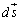 �������A�Ȑ�
�������A�Ȑ�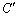 ���
���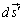 �������Ăł���Ǐ�̕Ȗʂ�U�Ƃ���ƁA
�������Ăł���Ǐ�̕Ȗʂ�U�Ƃ���ƁA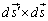 �͕Ȗ�U�̖ʐϑf��
�͕Ȗ�U�̖ʐϑf��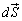 (�����͊Ǐ�ʂ���O�Ɍ����������ɂȂ�)�ł����āA2�̐��ϕ����ʐϕ��ɒu��������ƁA
(�����͊Ǐ�ʂ���O�Ɍ����������ɂȂ�)�ł����āA2�̐��ϕ����ʐϕ��ɒu��������ƁA
�E�ӂ̐ϕ������̊p��\���Ă��āA�A�ŁA���͐��o�H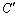 �ɉ����Đ��ϕ����Ă���ꍇ�ɂ́A�Ȗ�U��
�ɉ����Đ��ϕ����Ă���ꍇ�ɂ́A�Ȗ�U��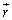 �̎n�_���܂�ł���̂ŁA
�̎n�_���܂�ł���̂ŁA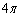 �ƂȂ�܂�(���́A���͐��ɉ����o�H�łȂ��Ă��A���̌o�H�ň͂ޖʂ��d�����т��Ă���悢)�B
�ƂȂ�܂�(���́A���͐��ɉ����o�H�łȂ��Ă��A���̌o�H�ň͂ޖʂ��d�����т��Ă���悢)�B
�� 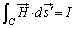
�@�̗��ӂ��A���͐��̌o�H�ł͂Ȃ��A�d���o�HC�����͂܂Ȃ��悤�Ȍo�H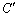 �ɂ��Đ��ϕ�����ꍇ�ɂ́A��L�̊Ǐ�Ȗʂ�
�ɂ��Đ��ϕ�����ꍇ�ɂ́A��L�̊Ǐ�Ȗʂ�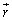 �̎n�_���܂܂Ȃ��̂ŁA�ʐϕ�
�̎n�_���܂܂Ȃ��̂ŁA�ʐϕ�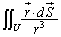 �̓[���ɂȂ�܂��B
�̓[���ɂȂ�܂��B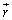 �̎n�_����Ȗ�U������Ƃ��A�߂����Ɖ������ƂŖʐϑf�Ђ��t�������A���̊p��\���ʐϕ���������������ł��B
�̎n�_����Ȗ�U������Ƃ��A�߂����Ɖ������ƂŖʐϑf�Ђ��t�������A���̊p��\���ʐϕ���������������ł��B
 �������āA���߂����E
�������āA���߂����E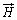 �̐��ϕ��̌o�H�ƂȂ�Ȑ���C�C���f��
�̐��ϕ��̌o�H�ƂȂ�Ȑ���C�C���f��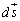 �Ə����ƁA
�Ə����ƁA
�Ȑ�C�̓������т��悤���d��I������Ă���Ƃ��ɂ́A
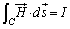 �@����D
�@����D
�ƂȂ�܂��B�D�����A���y�[������ϕ��̖@���ƌ����܂��B
�y�L���z��������L���ł��B�����̊F���܂̂��x�������������肽���A��낵�����肢�������܂��B
�y�L���z�L���͂����܂łł��B
�@�@������b����TOP�@�@����TOP�@�@TOP�y�[�W�ɖ߂�
�y�L���z��������L���ł��B�����̊F���܂̂��x�������������肽���A��낵�����肢�������܂��B
�y�L���z�L���͂����܂łł��B
�e���̒��쌠��
�o���w�ɑ����܂��B©2005-2024(�L)����� ��w�y�w�m ���������t���I���n��w�l�b�g�m��w�y�w�m(���ē���������)������́A
�܂��A������܂Ń��[����
�����肭�������B