�Q�[�W�ϊ�
�y�L���z��������L���ł��B�����̊F���܂̂��x�������������肽���A��낵�����肢�������܂��B
�y�L���z�L���͂����܂łł��B
��ԓ��̊e�_�ɂ����āA�d�E��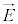 �C���E��
�C���E��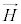 �C�U�d����ε�C��������μ�Ƃ��āA�d�����x��
�C�U�d����ε�C��������μ�Ƃ��āA�d�����x��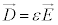 �C�������x��
�C�������x��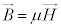 �C�܂��A�d�ז��x��ρ�C�d�����x��
�C�܂��A�d�ז��x��ρ�C�d�����x��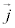 �Ƃ��āA
�Ƃ��āA
�}�N�X�E�G���̕������F
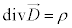 �@����@�@
�@����@�@
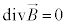 �@����A�@
�@����A�@
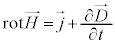 �@����B�@
�@����B�@
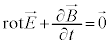 �@����C�@
�@����C�@
�Ȃ��A�B��div���Ƃ�ƁA�x�N�g����͂̌������A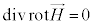 �ƂȂ�̂ŁA�@���A
�ƂȂ�̂ŁA�@���A
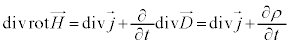 ��
�� 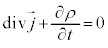 �@����D
�@����D
�@�`�C�ɂ��d����̋�������܂�킯�ł����A�d�E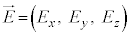 �C���E
�C���E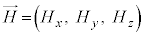 ��6�̎��R�x������̂ŁA�d�ו��zρ���d�����x
��6�̎��R�x������̂ŁA�d�ו��zρ���d�����x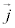 ��^���邾���ł́A�d�E
��^���邾���ł́A�d�E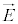 �C���E
�C���E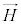 ����ӓI�ɋ��߂邱�Ƃ��ł��܂���B
����ӓI�ɋ��߂邱�Ƃ��ł��܂���B
�����ŁA�x�N�g���E�|�e���V����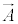 ��p���āA
��p���āA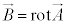 �ƕ\���邱�Ƃɒ��Ⴕ�܂��B
�ƕ\���邱�Ƃɒ��Ⴕ�܂��B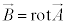 �̗��ӂ�div����p������ƁA
�̗��ӂ�div����p������ƁA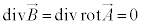 �ƂȂ�A�A�͎����I�ɖ�������܂��B
�ƂȂ�A�A�͎����I�ɖ�������܂��B
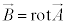 ���C�̍��ӂɑ������ƁA
���C�̍��ӂɑ������ƁA
�����ŁAϕ��K���Ȋ��Ƃ��āA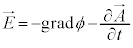 �Ƃ����ƁA
�Ƃ����ƁA
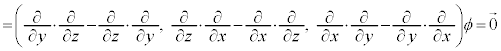 �@����E
�@����E
�ƂȂ��ćC����������܂��B
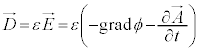 �C
�C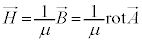 ���@�C�B�ɑ������ƁA
���@�C�B�ɑ������ƁA
�x�N�g����͂̌������A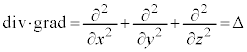 �C
�C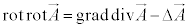 �ƂȂ�̂ŁA
�ƂȂ�̂ŁA
�F���A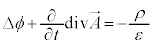 �@����H
�@����H
�G���A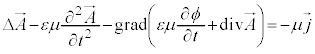 �@����I
�@����I
�H�C�I��p���āA�X�J���[��ϕ�C�x�N�g����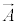 �����߂�A
�����߂�A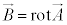 �C
�C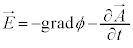 �ɂ��A���E
�ɂ��A���E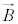 �C�d�E
�C�d�E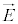 �����߂邱�Ƃ��ł���͂��ł��B
�����߂邱�Ƃ��ł���͂��ł��B
�Ƃ��낪�A�����œK���Ȋ�χ�������Ă��āA
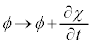 �C
�C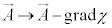 �@����J
�@����J
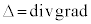 ���A
���A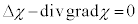 �Ȃ̂ŁA
�Ȃ̂ŁA
�܂��A�J���I�̍��ӂɑ�����Ă݂�ƁA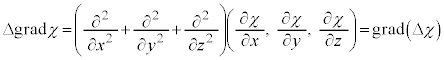 �Ȃ̂ŁA
�Ȃ̂ŁA
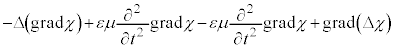 �@(��
�@(�� 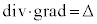 )
)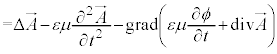 �@(�I�̍���)
�@(�I�̍���)
�܂��A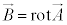 �C
�C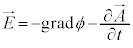 �ɂ����āA�J�Ƃ��Ă��A�E���A
�ɂ����āA�J�Ƃ��Ă��A�E���A
�ƂȂ�̂ŁA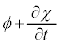 �C
�C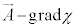 ��ϕ�C
��ϕ�C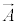 �̑���ɁA
�̑���ɁA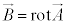 �C
�C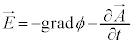 �ɑ�����Ă��A����
�ɑ�����Ă��A����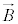 �C
�C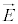 �������܂��B�܂�A�H�C�I�C����Maxwell�������ɂ́Aχ��K���Ȋ��Ƃ��āA�ϊ��J�Ɋւ��ĕs�ςł���A�Ƃ�������������܂��B���̕ϊ��J���Q�[�W�ϊ��A�Q�[�W�ϊ��ɂ���āA�d�E
�������܂��B�܂�A�H�C�I�C����Maxwell�������ɂ́Aχ��K���Ȋ��Ƃ��āA�ϊ��J�Ɋւ��ĕs�ςł���A�Ƃ�������������܂��B���̕ϊ��J���Q�[�W�ϊ��A�Q�[�W�ϊ��ɂ���āA�d�E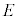 �C���E
�C���E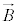 ���ς��Ȃ����Ƃ��A�Q�[�W�s���A�ƌ����܂��B
���ς��Ȃ����Ƃ��A�Q�[�W�s���A�ƌ����܂��B
�H�C�I�ł���χ�̕��������R�x���c��̂ŁAϕ�C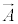 ���m�肳���邽�߂ɁA�H�C�I�ɏ����������邱�Ƃ��l���܂��B��́A���[�����c�E�Q�[�W�ƌĂ������F
���m�肳���邽�߂ɁA�H�C�I�ɏ����������邱�Ƃ��l���܂��B��́A���[�����c�E�Q�[�W�ƌĂ������F
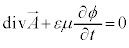 �@����K
�@����K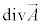 ��
��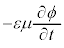 �Ƃ��A�I��grad�̃J�b�R�����[���Ƃ���ƁA�H�C�I�́A
�Ƃ��A�I��grad�̃J�b�R�����[���Ƃ���ƁA�H�C�I�́A
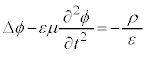 �@����L
�@����L
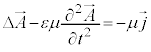 �@����M
�@����M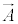 �̊e����
�̊e����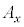 �C
�C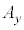 �C
�C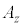 �ɂ��ē����`�̕������ɂȂ�܂��B�����ŁA
�ɂ��ē����`�̕������ɂȂ�܂��B�����ŁA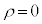 �C
�C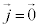 �Ƃ���ƁAϕ�C
�Ƃ���ƁAϕ�C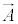 �ɑ����g���������ł��B
�ɑ����g���������ł��B
������A�N�[�����E�Q�[�W�ƌĂ������F
��t����ƁA�H�C�I�́A
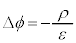 �@����N
�@����N
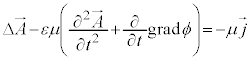 �@����O
�@����O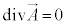 �����悤��
�����悤��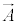 �����߁A
�����߁A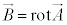 �C
�C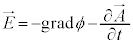 �ɂ��A���E
�ɂ��A���E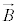 �C�d�E
�C�d�E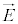 �����߂�A�Ƃ�������ɂȂ�܂��B
�����߂�A�Ƃ�������ɂȂ�܂��B
�y�L���z��������L���ł��B�����̊F���܂̂��x�������������肽���A��낵�����肢�������܂��B
�y�L���z�L���͂����܂łł��B
�@�@������b����TOP�@�@����TOP�@�@TOP�y�[�W�ɖ߂�
�y�L���z��������L���ł��B�����̊F���܂̂��x�������������肽���A��낵�����肢�������܂��B
�y�L���z�L���͂����܂łł��B
�e���̒��쌠��
�o���w�ɑ����܂��B©2005-2024(�L)����� ��w�y�w�m ���������t���I���n��w�l�b�g�m��w�y�w�m(���ē���������)������́A
�܂��A������܂Ń��[����
�����肭�������B 
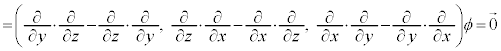 �@����E
�@����E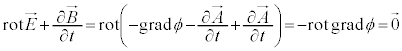
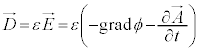 �C
�C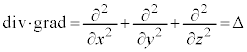 �C
�C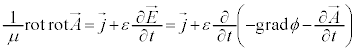
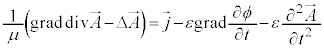 �@����G
�@����G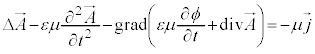 �@����I
�@����I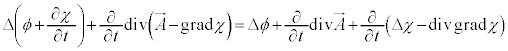
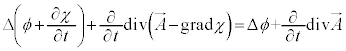
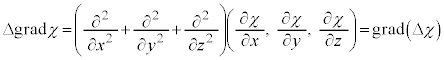 �Ȃ̂ŁA
�Ȃ̂ŁA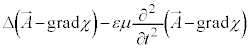
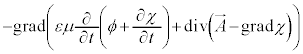
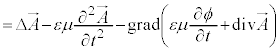
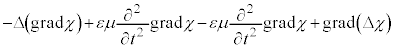 �@(��
�@(�� 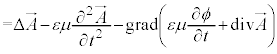 �@(�I�̍���)
�@(�I�̍���)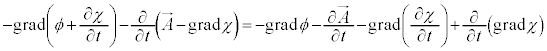
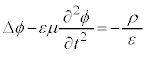 �@����L
�@����L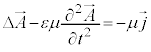 �@����M
�@����M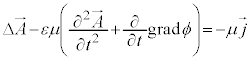 �@����O
�@����O