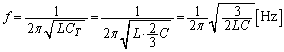横浜国大物理'09年[2]
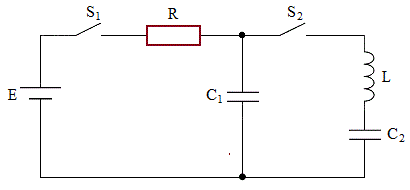 図に示すように、起電力
図に示すように、起電力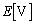 の電池E,抵抗値
の電池E,抵抗値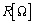 の抵抗R,電気容量
の抵抗R,電気容量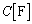 のコンデンサー
のコンデンサー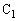 ,電気容量
,電気容量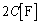 のコンデンサー
のコンデンサー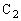 ,自己インダクタンス
,自己インダクタンス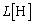 のコイルL,スイッチ
のコイルL,スイッチ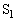 ,
,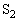 により構成された回路がある。初期状態ではスイッチ
により構成された回路がある。初期状態ではスイッチ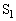 ,
,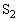 は開いていて、コンデンサー
は開いていて、コンデンサー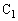 と
と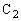 には電荷(電気量)がたまっていないものとする。また、電池とコイルの内部抵抗は無視できるものとする。以下の文章の空欄を埋めよ。
には電荷(電気量)がたまっていないものとする。また、電池とコイルの内部抵抗は無視できるものとする。以下の文章の空欄を埋めよ。
(1) スイッチ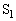 を閉じた直後に抵抗Rを流れる電流の大きさは ア [A]となる。また、十分に時間がたった後では、コンデンサー
を閉じた直後に抵抗Rを流れる電流の大きさは ア [A]となる。また、十分に時間がたった後では、コンデンサー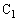 に蓄えられる電荷は イ [C],コンデンサー
に蓄えられる電荷は イ [C],コンデンサー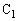 に蓄えられるエネルギーは ウ [J]となる。
に蓄えられるエネルギーは ウ [J]となる。 (2) 十分に時間がたった後でスイッチ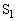 を開放し、スイッチ
を開放し、スイッチ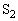 を閉じたところ、コイルの両端の電圧、各コンデンサーの両端の電圧、およびそれらを流れる電流は周期的に振動した。この振動の周波数は エ [Hz]である。
を閉じたところ、コイルの両端の電圧、各コンデンサーの両端の電圧、およびそれらを流れる電流は周期的に振動した。この振動の周波数は エ [Hz]である。 (3) スイッチ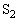 を閉じた直後は、コンデンサー
を閉じた直後は、コンデンサー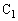 の極板間の電圧の大きさは
の極板間の電圧の大きさは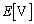 ,コンデンサー
,コンデンサー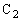 の極板間の電圧は
の極板間の電圧は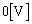 であるから、コイルLの両端の電圧の大きさは オ [V]と
であるから、コイルLの両端の電圧の大きさは オ [V]と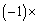 オ [V]の間を周期的に振動する。スイッチ
オ [V]の間を周期的に振動する。スイッチ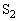 を閉じてから、コイルLの両端の電圧が最初に
を閉じてから、コイルLの両端の電圧が最初に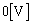 になるまでの時間は カ [s]となる。
になるまでの時間は カ [s]となる。 (4) コイルLの両端の電圧が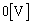 になった瞬間を考える。コンデンサー
になった瞬間を考える。コンデンサー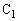 に蓄えられている電荷は キ [C],コンデンサー
に蓄えられている電荷は キ [C],コンデンサー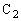 に蓄えられている電荷は ク [C]となり、コンデンサー
に蓄えられている電荷は ク [C]となり、コンデンサー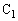 に蓄えられているエネルギーは ケ [J],コンデンサー
に蓄えられているエネルギーは ケ [J],コンデンサー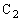 に蓄えられているエネルギーは コ [J]である。回路に蓄えられる電気エネルギーの総和は一定に保たれるので、コイルLに蓄えられているエネルギーは サ [J]となり、コイルLを流れる電流の大きさは シ [A]である。
に蓄えられているエネルギーは コ [J]である。回路に蓄えられる電気エネルギーの総和は一定に保たれるので、コイルLに蓄えられているエネルギーは サ [J]となり、コイルLを流れる電流の大きさは シ [A]である。
【広告】ここから広告です。ご覧の皆さまのご支援ご理解を賜りたく、よろしくお願いいたします。
【広告】広告はここまでです。
解答 コンデンサーとコイルに関する回路の問題ですが、単なる回路の問題とは言えない、慎重に考えるべき点のある問題です。
(2)(3)が見慣れない設定で悩みますが、問題文の(オ)の書き方がヒントになっています。
 (2)では、最初に
(2)では、最初に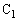 と
と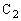 の間の部分の電荷が0でないので、
の間の部分の電荷が0でないので、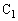 と
と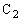 は直列ではなく、L両端、即ち、
は直列ではなく、L両端、即ち、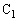 と
と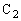 両端の電圧をV,
両端の電圧をV,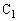 が蓄える電荷をQとして、
が蓄える電荷をQとして、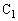 と
と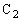 を直列として考えた合成容量
を直列として考えた合成容量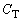 (
(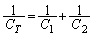 )との間に、
)との間に、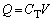 という関係は成立しません。
という関係は成立しません。
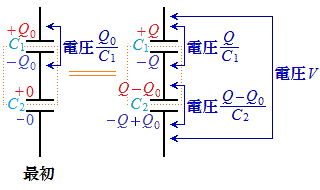
どういうことかと言うと、右図で、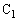 に最初電荷
に最初電荷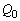 が蓄えられていて、
が蓄えられていて、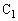 と
と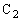 両端の電圧をVとしたときの
両端の電圧をVとしたときの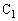 の電荷をQとすると、
の電荷をQとすると、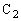 の
の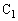 側の極板の電荷
側の極板の電荷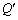 は、電荷保存より、
は、電荷保存より、
∴ 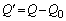
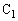 両端の電圧
両端の電圧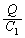 と
と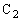 両端の電圧
両端の電圧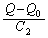 の和がVになるので、
の和がVになるので、
∴ 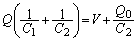
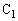 と
と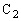 直列の合成容量
直列の合成容量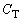 を用いて、
を用いて、
つまり、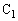 と
と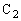 が直列であるときには、
が直列であるときには、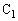 と
と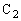 には等量の電荷が蓄えられるはずなのですが、
には等量の電荷が蓄えられるはずなのですが、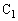 と
と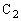 の間に孤立している電荷
の間に孤立している電荷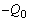 があると、電圧が
があると、電圧が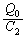 だけずれるので、直列の公式通りにならなくなります。
だけずれるので、直列の公式通りにならなくなります。
ですが、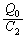 は定数なので、振動回路においては、
は定数なので、振動回路においては、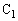 と
と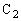 の間に孤立している電荷は振動中心と振幅を変化させても、周波数には影響を与えません。従って、(3)の振動回路では、
の間に孤立している電荷は振動中心と振幅を変化させても、周波数には影響を与えません。従って、(3)の振動回路では、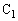 と
と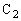 を直列として合成容量を考え、周波数を求めることができます。
を直列として合成容量を考え、周波数を求めることができます。
(1)(ア) 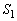 を閉じた直後、
を閉じた直後、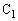 は導通したのと同じで、電流の大きさは、オームの法則より、
は導通したのと同じで、電流の大きさは、オームの法則より、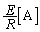
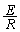 ......[答]
......[答](イ) 十分時間が経過すると、電流は流れなくなりR両端の電圧は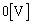 で、
で、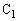 に蓄えられる電荷は、
に蓄えられる電荷は、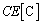
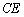 ......[答]
......[答]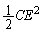 ......[答]
......[答]
振動の周波数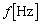 は、
は、
(3)(オ) スイッチ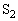 を閉じた直後、問題文より、コイルLの両端の電圧の大きさは
を閉じた直後、問題文より、コイルLの両端の電圧の大きさは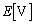 (問題文の図のL上側が高電位)で、コイルL両端の電圧は、
(問題文の図のL上側が高電位)で、コイルL両端の電圧は、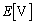 と
と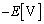 の間で振動します。
の間で振動します。 E ......[答]
(カ) スイッチ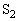 を閉じてから、コイルLの両端の電圧が最初に
を閉じてから、コイルLの両端の電圧が最初に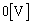 になるまでの時間は、単振動の周期
になるまでの時間は、単振動の周期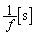 の
の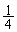 に等しく、
に等しく、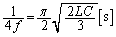
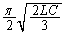 ......[答]
......[答]
(4)(キ) L両端の電圧が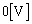 になった瞬間に、
になった瞬間に、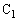 に蓄えられている電荷を
に蓄えられている電荷を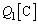 として、電荷保存より、
として、電荷保存より、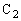 の上側の極板には、
の上側の極板には、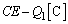 の電荷が蓄えられています。このとき、
の電荷が蓄えられています。このとき、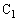 両端の電圧と
両端の電圧と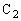 両端の電圧が等しくなるので、
両端の電圧が等しくなるので、 ∴ 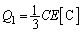
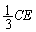 ......[答]
......[答] (ク) 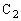 に蓄えられている電荷は、
に蓄えられている電荷は、 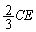 ......[答]
......[答](ケ) 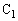 に蓄えられているエネルギーは、
に蓄えられているエネルギーは、 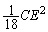 ......[答]
......[答](コ) 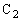 に蓄えられているエネルギーは、
に蓄えられているエネルギーは、 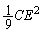 ......[答]
......[答](サ) エネルギー保存より、Lに蓄えられているエネルギーは、
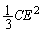 ......[答]
......[答](シ) このときの電流の大きさを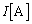 として、Lに蓄えられているエネルギーは、
として、Lに蓄えられているエネルギーは、 ∴ 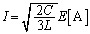
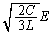 ......[答]
......[答] 注.この電流の大きさが、電流の単振動の振幅であり、電流の最大値になります。また、この問題では、電流の最大値Iについて、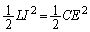 (最初の
(最初の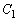 の静電エネルギー)とならないので注意してください。
の静電エネルギー)とならないので注意してください。
(5)(ス) 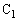 に蓄えられる電荷が
に蓄えられる電荷が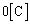 になった瞬間に、
になった瞬間に、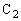 に蓄えられている電荷は、電荷保存より
に蓄えられている電荷は、電荷保存より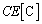 です。
です。 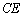 ......[答]
......[答](セ) 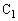 両端の電圧は
両端の電圧は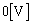 で、L両端の電圧の大きさは、
で、L両端の電圧の大きさは、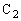 両端の電圧の大きさに等しく、
両端の電圧の大きさに等しく、 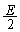 ......[答]
......[答](ソ) 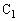 に蓄えられているエネルギーは
に蓄えられているエネルギーは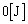 ,
,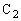 に蓄えられているエネルギーは
に蓄えられているエネルギーは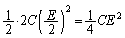 で、コイルに流れる電流を
で、コイルに流れる電流を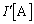 として、エネルギー保存より、
として、エネルギー保存より、 ∴ 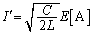
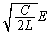 ......[答]
......[答]
【広告】ここから広告です。ご覧の皆さまのご支援ご理解を賜りたく、よろしくお願いいたします。
【広告】広告はここまでです。
物理TOP TOPページに戻る
【広告】ここから広告です。ご覧の皆さまのご支援ご理解を賜りたく、よろしくお願いいたします。
【広告】広告はここまでです。
各問題の著作権は
出題大学に属します。©2005-2024(有)りるらる 苦学楽学塾 随時入会受付中!理系大学受験ネット塾苦学楽学塾(ご案内はこちら)ご入会は、
まず、こちらまでメールを
お送りください。