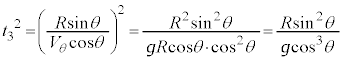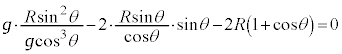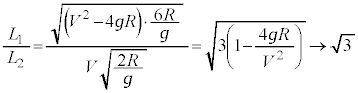���啨��'22�N�O��[1]
���̕��͂�ǂ�ŁA �ɓK�������܂��͐��l���A���ꂼ��̉��ɋL������B�Ȃ��A
�ɓK�������܂��͐��l���A���ꂼ��̉��ɋL������B�Ȃ��A �͂��ł�
�͂��ł� �ŗ^����ꂽ���̂Ɠ������̂�\���B�܂��A��1�C��2�ł́A�w���ɂ��������āA�����ꂼ��̉��ɋL������B�������A�d�͉����x�̑傫����
�ŗ^����ꂽ���̂Ɠ������̂�\���B�܂��A��1�C��2�ł́A�w���ɂ��������āA�����ꂼ��̉��ɋL������B�������A�d�͉����x�̑傫����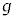 �Ƃ��A���C���C��R�A�����̑傫���Ɖ�]�̉e���͖������A�Փ˂͂��ׂĊ��S�e���Փ˂Ƃ���B
�Ƃ��A���C���C��R�A�����̑傫���Ɖ�]�̉e���͖������A�Փ˂͂��ׂĊ��S�e���Փ˂Ƃ���B
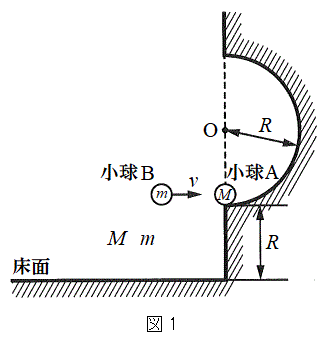 �}1�̂悤�ɁA�����ȕǂ�����A�����ȏ��ʂ��獂��R�̈ʒu����ɂ͓_O�𒆐S�Ƃ��锼�aR�̔��~����̂��ڂ݂�����B���~���̉��[�Ɏ���M�̏���A���Î~���Ă���A�����玿��m�̏���B�𑬂�v�Ő����ɏՓ˂�����B�Փ˂ɂ���ď���A�͐��������̑���V�āA���~���ɉ��������炩�ȉ^�����J�n����B�^���͂��ׂē��ꉔ���ʓ�(���Ȃ킿�A�}1�̎��ʓ�)�ŋN���Ă�����̂Ƃ���B
�}1�̂悤�ɁA�����ȕǂ�����A�����ȏ��ʂ��獂��R�̈ʒu����ɂ͓_O�𒆐S�Ƃ��锼�aR�̔��~����̂��ڂ݂�����B���~���̉��[�Ɏ���M�̏���A���Î~���Ă���A�����玿��m�̏���B�𑬂�v�Ő����ɏՓ˂�����B�Փ˂ɂ���ď���A�͐��������̑���V�āA���~���ɉ��������炩�ȉ^�����J�n����B�^���͂��ׂē��ꉔ���ʓ�(���Ȃ킿�A�}1�̎��ʓ�)�ŋN���Ă�����̂Ƃ���B
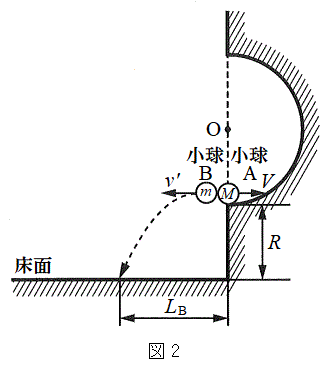 (1) �}2�̂悤�ɏ���B������
(1) �}2�̂悤�ɏ���B������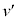 �ō������ɒ��˕Ԃ����Ƃ��A�^���ʕۑ��̖@������
�ō������ɒ��˕Ԃ����Ƃ��A�^���ʕۑ��̖@���������A�͊w�I�G�l���M�[�ۑ��̖@������
����������̂ŁAm�CM�CV��p����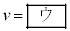 �C
�C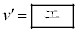 �ƕ\����B������A����B���������ɒ��˕Ԃ���������M��m��p����
�ƕ\����B������A����B���������ɒ��˕Ԃ���������M��m��p���� �ƕ\����B����ɁA����B�����ʂɗ�������n�_�ƕǂ̋���
�ƕ\����B����ɁA����B�����ʂɗ�������n�_�ƕǂ̋���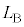 ���Am�CM�CV�CR�C
���Am�CM�CV�CR�C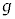 ��p����
��p����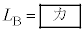 �ƕ\����B
�ƕ\����B
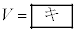 �̂Ƃ��A����A�͔��~���̒��SO�Ɠ��������܂œo��B�܂�A
�̂Ƃ��A����A�͔��~���̒��SO�Ɠ��������܂œo��B�܂�A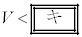 �̂Ƃ��A����A�͔��~���̒��SO�����Ⴂ�����܂œo�����̂��ɔ��~���ɉ����ĉ����Ă���B�����Ĕ��~���̒[�����������`���ď��ʂɗ�������B�����ŁA����A�̗����n�_������B�̗����n�_�Ɠ����ł���Ƃ��AM��m�̊W��
�̂Ƃ��A����A�͔��~���̒��SO�����Ⴂ�����܂œo�����̂��ɔ��~���ɉ����ĉ����Ă���B�����Ĕ��~���̒[�����������`���ď��ʂɗ�������B�����ŁA����A�̗����n�_������B�̗����n�_�Ɠ����ł���Ƃ��AM��m�̊W�� �ƕ\����B
�ƕ\����B
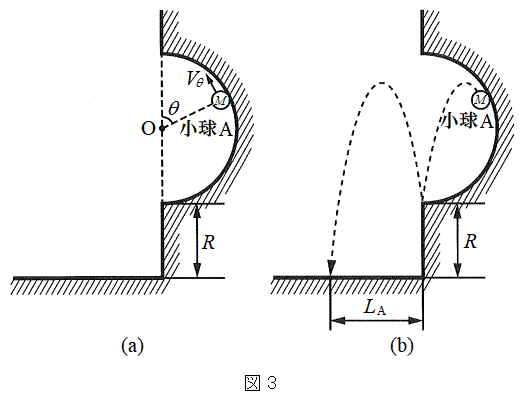 (2) �}3(a)�̂悤�ɁA����A�����~���̒��SO���������ʒu�܂œo��A�p�xθ�̂Ƃ��ɔ��~���̕ǂ��痣���Ƃ���B�����u�Ԃɂ����鏬��A�̑���
(2) �}3(a)�̂悤�ɁA����A�����~���̒��SO���������ʒu�܂œo��A�p�xθ�̂Ƃ��ɔ��~���̕ǂ��痣���Ƃ���B�����u�Ԃɂ����鏬��A�̑���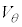 ��
��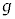 �CR�C�p����
�CR�Cθ��p����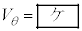 �ƕ\�����B���̂Ƃ��A�Փ˒���̑���V�����l��
�ƕ\�����B���̂Ƃ��A�Փ˒���̑���V�����l��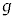 �CR�Cθ��p����
�CR�Cθ��p����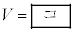 �ƕ\����B
�ƕ\����B���ɁA�}3(b)�̂悤�ɁA���~���̕ǂ��痣�ꂽ����A���A�͂��߂ɐÎ~���Ă����ʒu(���~���̉��̒[�̈ʒu)�ɗ������A�����Œ��˕Ԃ��ď��ʂɗ�������ꍇ���l����B����A�����˕Ԃ�ʂ͐����ƌ��Ȃ��B
����A���͂��߂ɐÎ~���Ă����ʒu�ɗ�������̂�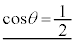 �̏ꍇ�݂̂ł���B�����p����ƁA�͂��߂̈ʒu�ɗ������钼�O�ɂ����鏬��A�̐��������������̑���
�̏ꍇ�݂̂ł���B�����p����ƁA�͂��߂̈ʒu�ɗ������钼�O�ɂ����鏬��A�̐��������������̑���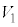 �́A
�́A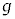 ��R��p����
��R��p����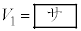 �ƕ\���A���������������̑���
�ƕ\���A���������������̑���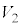 ��
��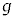 ��R��p����
��R��p����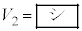 �ƕ\����B�����āA����A�����ʂɗ�������n�_�ƕǂ̋���
�ƕ\����B�����āA����A�����ʂɗ�������n�_�ƕǂ̋���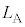 ��
��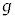 �CR�C
�CR�C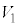 �C
�C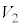 ��p����
��p����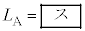 �ƕ\����B
�ƕ\����B
��1�@�������ŏq�ׂ��悤�ɁA����A���͂��߂ɐÎ~���Ă����ʒu�ɗ�������̂�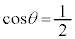 �̏ꍇ�݂̂ł��邱�Ƃ������B
�̏ꍇ�݂̂ł��邱�Ƃ������B
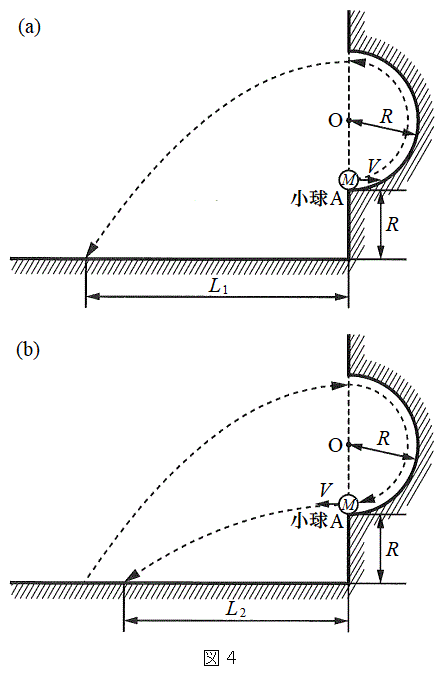 (3) ����V���\���ɑ傫���ꍇ���l����B����A�͐}4(a)�̂悤�ɔ��~���̏�[���琅�����˂���A�ǂ��狗��
(3) ����V���\���ɑ傫���ꍇ���l����B����A�͐}4(a)�̂悤�ɔ��~���̏�[���琅�����˂���A�ǂ��狗��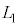 �̏��ʂɗ�������B����A���������Ƃ��̑����Ɗp�x�ŁA���������ʒu���珬��A���t�����ɓ����Ԃ��ƁA�}4(b)�̂悤�ɔ��~�����t�����Ɏ���A���[���瑬��V�Ő������˂���A�ǂ��狗��
�̏��ʂɗ�������B����A���������Ƃ��̑����Ɗp�x�ŁA���������ʒu���珬��A���t�����ɓ����Ԃ��ƁA�}4(b)�̂悤�ɔ��~�����t�����Ɏ���A���[���瑬��V�Ő������˂���A�ǂ��狗��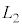 ���ꂽ�ʒu�ŏ��ʂɗ�������B
���ꂽ�ʒu�ŏ��ʂɗ�������B
��2�@�����2�̋����̔�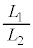 �́A����V���傫���Ȃ�ɂ��
�́A����V���傫���Ȃ�ɂ��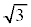 �ɋ߂Â��B���̗��R���Ȍ��ɏq�ׂ�B
�ɋ߂Â��B���̗��R���Ȍ��ɏq�ׂ�B
�y�L���z��������L���ł��B�����̊F���܂̂��x�������������肽���A��낵�����肢�������܂��B
�y�L���z�L���͂����܂łł��B
���@�~�^���A�ՓˁA�������˂̗Z�����ł��B
(1) �ՓˑO���^�����́A����B�̉E�����^����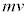 �C�Փˌ�̉^���ʂ́A����B�̍������̉^����
�C�Փˌ�̉^���ʂ́A����B�̍������̉^����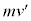 �C����A�̉E�����̉^����
�C����A�̉E�����̉^����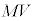 �ł��B�^���ʕۑ����A
�ł��B�^���ʕۑ����A 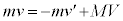 �@����@�@
�@����@�@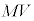 ......[�A]
......[�A]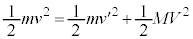 �@����A�@
�@����A�@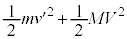 ......[�C]
......[�C]�@���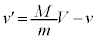 �@����B
�@����B
�A�ɑ������ƁA ��������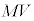 �Ŋ���ƁA
�Ŋ���ƁA 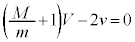 �@��
�@�� 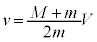 ......[�E]
......[�E]�B���A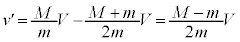 ......[�G]�@����C
......[�G]�@����C
�������ɒ��˕Ԃ��������́A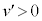 ���A
���A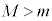 ......[�I]����������R�������鎞�Ԃ�
......[�I]����������R�������鎞�Ԃ�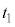 �Ƃ��āA�������x�^���̌������A
�Ƃ��āA�������x�^���̌������A 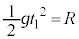 �@��
�@�� 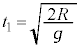 �@����D
�@����D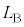 �́A���������ɑ���
�́A���������ɑ���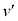 �Ŏ���
�Ŏ���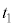 �i�ދ����Ƃ��āA
�i�ދ����Ƃ��āA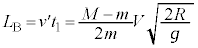 ......[�J]
......[�J]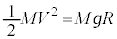 �@��
�@�� 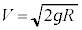 ......[�L]
......[�L]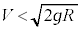 �̂Ƃ��A����A���Փ˒n�_�ɖ߂��Ă����Ƃ��̑�����V�ł��B����A�̗����n�_������B�̗����n�_�Ɠ����ł�������́A
�̂Ƃ��A����A���Փ˒n�_�ɖ߂��Ă����Ƃ��̑�����V�ł��B����A�̗����n�_������B�̗����n�_�Ɠ����ł�������́A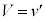 ���A�C��p���āA
���A�C��p���āA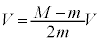 �@��
�@�� 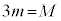 ......[�N]
......[�N]
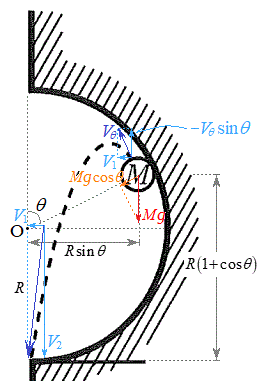 (2) �p�xθ�̂Ƃ��A����A���ǂ��痣���̂ŏ���A���ǂ���鐂���R�͂�0�ł��B�~�^�����鏬��A�ɓ������S�͂͏���A�ɓ����d�͂�O�Ɍ����������ʼnE�}���
(2) �p�xθ�̂Ƃ��A����A���ǂ��痣���̂ŏ���A���ǂ���鐂���R�͂�0�ł��B�~�^�����鏬��A�ɓ������S�͂͏���A�ɓ����d�͂�O�Ɍ����������ʼnE�}���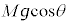 �C�~�^���̉^��������(�s�����~�^�����Q��)�́A
�C�~�^���̉^��������(�s�����~�^�����Q��)�́A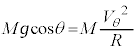 �@����E�@��
�@����E�@�� 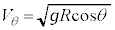 ......[�P]
......[�P]�p�xθ�̂Ƃ��A�^���G�l���M�[��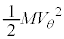 �C�Փ˒n�_����̍����͉E�}���
�C�Փ˒n�_����̍����͉E�}���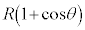 �ňʒu�G�l���M�[��
�ňʒu�G�l���M�[��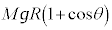 �C�Փ˒n�_�Ƃ��͊w�I�G�l���M�[�ۑ����A
�C�Փ˒n�_�Ƃ��͊w�I�G�l���M�[�ۑ����A �E���A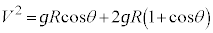 �@��
�@�� 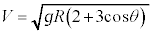 ......[�R]�͂��߂̈ʒu�ɗ������钼�O�ɂ����鏬��A�̐��������������̑���
......[�R]�͂��߂̈ʒu�ɗ������钼�O�ɂ����鏬��A�̐��������������̑���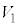 �C���������������̑���
�C���������������̑���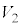 �́A�p�xθ�̂Ƃ��̏���A�̑��x�̐�������������
�́A�p�xθ�̂Ƃ��̏���A�̑��x�̐�������������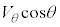 �C���������������������𐳂Ƃ���
�C���������������������𐳂Ƃ���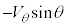 �ł����āA
�ł����āA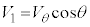 �C�܂��A�������x�^���̌������A
�C�܂��A�������x�^���̌������A 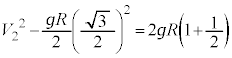 �@��
�@�� 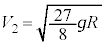 ......[�V]
......[�V]�͂��߂̈ʒu�ɗ������Ċ��S�e���Փˌ�̏���A�̑��x�͉������𐳂Ƃ���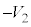 �ł��B���ɗ�������܂ł̎��Ԃ�
�ł��B���ɗ�������܂ł̎��Ԃ�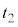 �Ƃ��āA�������x�^���̌������A
�Ƃ��āA�������x�^���̌������A ���ʂɗ�������n�_�ƕǂƂ̋���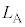 �́A����
�́A����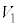 �Ŏ���
�Ŏ���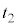 �i�ދ����Ƃ��āA
�i�ދ����Ƃ��āA 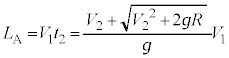 ......[�X]
......[�X]
��1�@(2)�̐}���A�p�xθ�̂Ƃ��ɕǂ��痣��āA���������ɁA����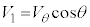 �Ŏ���
�Ŏ���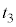 �C����
�C����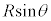 �����ړ�����ԂɁA���������ɁA�����x
�����ړ�����ԂɁA���������ɁA�����x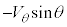 ��
��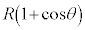 �������Ă͂��߂̈ʒu�ɗ��܂��B�������x�^���̌������A
�������Ă͂��߂̈ʒu�ɗ��܂��B�������x�^���̌������A 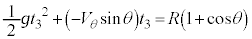 �@����F
�@����F�܂��A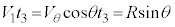 �@��
�@�� 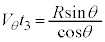
[�P]�̌��ʂ�p���āA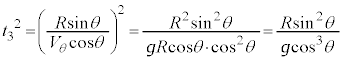
�������F�ɑ�����āA �������āA
�� 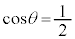 ����āA����A���͂��߂ɐÎ~���Ă����ʒu�ɗ�������̂�
����āA����A���͂��߂ɐÎ~���Ă����ʒu�ɗ�������̂�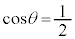 �̏ꍇ�݂̂ł��B
�̏ꍇ�݂̂ł��B
(3) ���~���̏�[���琅�����˂���ꍇ�A����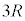 �������鎞��
�������鎞��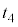 �́A
�́A 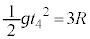 �@��
�@�� 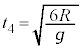
�ŏ�[�ł̑�����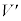 �Ƃ���ƁA�ŏ�[�ƏՓ˒���Ƃ̗͊w�I�G�l���M�[�ۑ����A
�Ƃ���ƁA�ŏ�[�ƏՓ˒���Ƃ̗͊w�I�G�l���M�[�ۑ����A 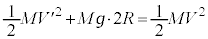 �@��
�@�� 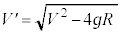
����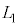 �͑���
�͑���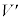 �Ŏ���
�Ŏ���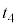 �i�ދ����Ƃ��āA
�i�ދ����Ƃ��āA �ŏ��̈ʒu���琅�����˂���ꍇ�A����R�������鎞�Ԃ�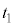 �ŁA����
�ŁA����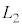 �͑���V�Ŏ���
�͑���V�Ŏ���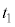 �i�ދ����Ƃ��āA�D��p���āA
�i�ދ����Ƃ��āA�D��p���āA
��2�@�ȏ���A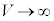 �̂Ƃ��A
�̂Ƃ��A �ƂȂ�̂ł����A���R���Ȍ��ɏq�ׂ�A�Ƃ������ƂȂ̂ŁA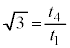 �ł��邱�Ƃ���A
�ł��邱�Ƃ���A V���傫���Ȃ�ƁA�����̈Ⴂ�ɂ�鏉���x�̈Ⴂ���Ȃ��Ȃ�A�������B�������������˂̗������Ԃɔ�Ⴕ�A�������Ԃ�������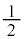 ��Ɉˑ����A�����̔䂪3�{�Ȃ̂ŁA���B�����̔��
��Ɉˑ����A�����̔䂪3�{�Ȃ̂ŁA���B�����̔��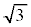 �ɋ߂Â� ......[��]
�ɋ߂Â� ......[��]
�y�L���z��������L���ł��B�����̊F���܂̂��x�������������肽���A��낵�����肢�������܂��B
�y�L���z�L���͂����܂łł��B
�@�@���啨��TOP�@�@����TOP�@�@TOP�y�[�W�ɖ߂�
�y�L���z��������L���ł��B�����̊F���܂̂��x�������������肽���A��낵�����肢�������܂��B
�y�L���z�L���͂����܂łł��B
�e���̒��쌠��
�o���w�ɑ����܂��B©2005-2024(�L)����� ��w�y�w�m ���������t���I���n��w�l�b�g�m��w�y�w�m(���ē���������)������́A
�܂��A������܂Ń��[����
�����肭�������B  �@��
�@�� 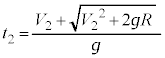 (
(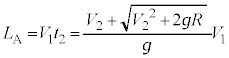 ......[�X]
......[�X]