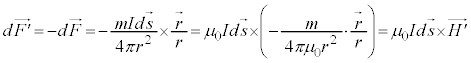�d���E�דd���q�����
�y�L���z��������L���ł��B�����̊F���܂̂��x�������������肽���A��낵�����肢�������܂��B
�y�L���z�L���͂����܂łł��B
�������x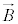 �����E���𗬂�������d��
�����E���𗬂�������d��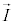 ������l�̕����ɓ�����
������l�̕����ɓ�����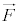 �́A
�́A
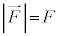 �C
�C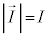 �C
�C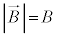 �C
�C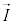 ��
��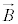 �̂Ȃ��p��θ �Ƃ��āA
�̂Ȃ��p��θ �Ƃ��āA
�d�E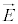 ���������x
���������x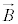 �����E�����݂��钆�����x
�����E�����݂��钆�����x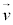 �Œʉ߂����דd���qq�������A�������[�����c��
�Œʉ߂����דd���qq�������A�������[�����c��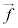 �́A
�́A
�d�E�����݂��Ȃ��ꍇ�A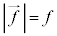 �C
�C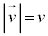 �C���x
�C���x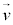 ���������x
���������x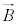 �̂Ȃ��p��θ �Ƃ��āA
�̂Ȃ��p��θ �Ƃ��āA
�P�ꎥ���̑��݂͔ے肳��Ă���̂ł����A�����ł́A���C�o�Ɏq�̕Б��������ɓ������ɂ��čl���Ă݂܂��B���C�̊�{�P�ʂ�������~�`�d���ƍl����ꍇ�ł��A�������~�`�d���͎��C�o�Ɏq�Ɠ����Ȃ̂�(���C�o�Ɏq���Q��)�A�~�`�d���Ɠ����Ȏ��C�o�Ɏq�̕Б����������l���邱�Ƃɂ��܂��B
���E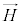 ���ɒu���ꂽ�_����m�ɓ������F
���ɒu���ꂽ�_����m�ɓ������F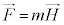 (���E���Q��)���r�I�E�T�o�[���̖@���ɂ��A�d���f��
(���E���Q��)���r�I�E�T�o�[���̖@���ɂ��A�d���f��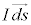 ��
��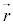 ���ꂽ�ʒu�ɍ���������E�F
���ꂽ�ʒu�ɍ���������E�F
�̒����_����m��u���ƁA�����_�����ɂ́A
�Ƃ������������܂��B��p����p�̖@�����l����ƁA�_����m�̍�����E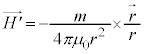 (���C�ɂ�����N�[�����̖@�����Q��)���d���f��
(���C�ɂ�����N�[�����̖@�����Q��)���d���f��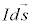 �ɋy�ڂ���
�ɋy�ڂ���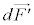 �́A
�́A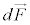 �Ƒ傫���������������͋t�ŁA
�Ƒ傫���������������͋t�ŁA
���̎��́A�_����m�̍�����E���𗬂���d�������łȂ��A(���C�o�Ɏq�̑�����������܂߂�)�_�������u���Ăł������E���d�ˍ��킹��A�C�ӂ����E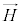 ���𗬂���d���ɓ�����
���𗬂���d���ɓ�����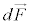 �ɂ��Ă��������܂��B�܂�A
�ɂ��Ă��������܂��B�܂�A
����l�������d�������E���y�ڂ��͂̑傫��F�́A
�������x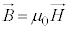 �Ǝg���ď����ƁA�����d�����������܂߂�
�Ǝg���ď����ƁA�����d�����������܂߂�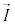 �Ƃ��āA
�Ƃ��āA
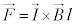 �@����@
�@����@
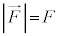 �C
�C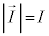 �C
�C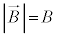 �C�d��
�C�d��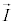 ���������x
���������x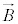 �̂Ȃ��p��θ �Ƃ��āA
�̂Ȃ��p��θ �Ƃ��āA
�����ŁA����l�C�f�ʐ�S�̒�����̓��̖_���ɁA�d��q�����דd���q�����xn (�P�ʑ̐ϒ���n��)�ő��݂��A���̖_�������x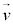 �Œʉ߂��邱�Ƃɂ���d��
�Œʉ߂��邱�Ƃɂ���d��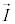 �������Ƃ��܂��B���̂Ƃ��A
�������Ƃ��܂��B���̂Ƃ��A
�ł��B������@�ɑ������ƁA
�������x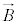 �����E�������x
�����E�������x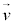 �Œʉ߂����דd���qq������
�Œʉ߂����דd���qq������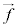 �́A�d���̎���
�́A�d���̎���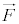 �̖_���̉דd���q�̌�
�̖_���̉דd���q�̌�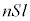 �Ŋ����āA
�Ŋ����āA
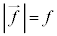 �C
�C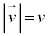 �C���x
�C���x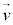 ���������x
���������x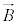 �̂Ȃ��p��θ �Ƃ��āA
�̂Ȃ��p��θ �Ƃ��āA
���Z�͈̔͂ł́A�����������[�����c���ƌ����Ă��܂����A���̉^�������x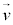 �ʼn^������ϑ��҂��猩��ƁA�דd���q���Î~���Ă���̂�������悤�Ɍ����܂��B�A�C���V���^�C���́A������A���x
�ʼn^������ϑ��҂��猩��ƁA�דd���q���Î~���Ă���̂�������悤�Ɍ����܂��B�A�C���V���^�C���́A������A���x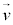 �ʼn^������ϑ��҂��猩��Ƃ��ɂ́A�U���d�E
�ʼn^������ϑ��҂��猩��Ƃ��ɂ́A�U���d�E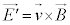 ���ł��Ă��āA�דd���q�͂����d�E����������̂��A�Ɛ������܂����B
���ł��Ă��āA�דd���q�͂����d�E����������̂��A�Ɛ������܂����B
�܂�A�N�[������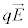 ���U���d�E�ɂ����
���U���d�E�ɂ����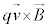 �́A�ϑ��҂̗���ɂ���ĕς���Ă��܂����̂ł����Ė{����ʂł��Ȃ��̂ł��B�d�E
�́A�ϑ��҂̗���ɂ���ĕς���Ă��܂����̂ł����Ė{����ʂł��Ȃ��̂ł��B�d�E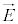 �C�������x
�C�������x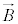 �̎��E�������x
�̎��E�������x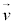 �ʼn^�������דd���qq�̎���
�ʼn^�������דd���qq�̎���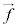 �́A
�́A
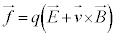 �@����A
�@����A
�y�L���z��������L���ł��B�����̊F���܂̂��x�������������肽���A��낵�����肢�������܂��B
�y�L���z�L���͂����܂łł��B
�@�@������b����TOP�@�@����TOP�@�@TOP�y�[�W�ɖ߂�
�y�L���z��������L���ł��B�����̊F���܂̂��x�������������肽���A��낵�����肢�������܂��B
�y�L���z�L���͂����܂łł��B
�e���̒��쌠��
�o���w�ɑ����܂��B©2005-2024(�L)����� ��w�y�w�m ���������t���I���n��w�l�b�g�m��w�y�w�m(���ē���������)������́A
�܂��A������܂Ń��[����
�����肭�������B 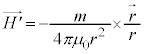 (���C�ɂ�����N�[�����̖@�����Q��)���d���f��
(���C�ɂ�����N�[�����̖@�����Q��)���d���f��