���H�啨��'02�N�O��[3]
 �@����m�̏����̗����Ɏ��R����
�@����m�̏����̗����Ɏ��R����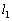 �̃S���Ђ�1��
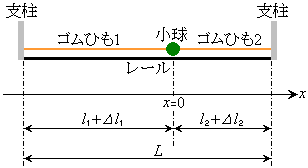
�̃S���Ђ�1��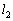 �̃S���Ђ�2�̈�[���Ȃ��A�}�̂悤�ɂ��̏����𐅕��ɒu���ꂽ����L�̐^�������ȃ��[���̏�ɒu���B2�{�̃S���Ђ��̑��[�́A���[���̗��[�ɌŒ肳�ꂽ�x���ɂȂ����B���̂Ƃ�������̃S���Ђ������R�������L�тĂ����B�S���Ђ������R������
�̃S���Ђ�2�̈�[���Ȃ��A�}�̂悤�ɂ��̏����𐅕��ɒu���ꂽ����L�̐^�������ȃ��[���̏�ɒu���B2�{�̃S���Ђ��̑��[�́A���[���̗��[�ɌŒ肳�ꂽ�x���ɂȂ����B���̂Ƃ�������̃S���Ђ������R�������L�тĂ����B�S���Ђ������R������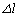 �����L����
�����L����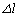 �ɔ�Ⴗ�镜���͂������B�����͂̔��萔�́A�S���Ђ�1�ł�k�C�S���Ђ�2�ł�
�ɔ�Ⴗ�镜���͂������B�����͂̔��萔�́A�S���Ђ�1�ł�k�C�S���Ђ�2�ł�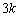 �ł���B�}�̂悤�ɂ肠���̈ʒu��x���̌��_�Ƃ��A�S���Ђ�2�̂���E������x���̐��̌����Ƃ��ď����̈ʒu��x�ŕ\�����̂Ƃ���B�Ȃ��A�����́A���[���̏�C�Ȃ��^��������̂Ƃ��A����S���Ђ��ɂ��^�����W�����邱�Ƃ͂Ȃ����̂Ƃ���B�܂��A�S���Ђ��̎��ʂ͖����ł�����̂Ƃ���B
�ł���B�}�̂悤�ɂ肠���̈ʒu��x���̌��_�Ƃ��A�S���Ђ�2�̂���E������x���̐��̌����Ƃ��ď����̈ʒu��x�ŕ\�����̂Ƃ���B�Ȃ��A�����́A���[���̏�C�Ȃ��^��������̂Ƃ��A����S���Ђ��ɂ��^�����W�����邱�Ƃ͂Ȃ����̂Ƃ���B�܂��A�S���Ђ��̎��ʂ͖����ł�����̂Ƃ���B
[A]�@���������_�ɂ���ꍇ�ɂ��čl����B
(a) �S���Ђ�1��2�̂��ꂼ��̎��R������̐L��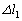 ��
��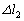 �����߂�B
�����߂�B
[B]�@������x�܂ŕψʂ������Ƃ�������2�{�̃S���Ђ�����鍇��F���l����B�Ȃ��A��F�̕����́Ax���̌����Ɠ��l�ɉE�����𐳂Ƃ���B
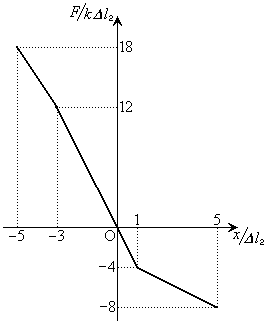
(b) F��x�̊W��\���O���t��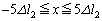 �̗̈�ɂ��Ď����B�Ȃ��A���͈̔͂̕ψʂł́A�����͎x���ɂԂ���Ȃ����̂Ƃ���B�܂��A���ėp���̃O���t�ł́A�ψʂƗ͂̒P�ʂ����ꂼ��
�̗̈�ɂ��Ď����B�Ȃ��A���͈̔͂̕ψʂł́A�����͎x���ɂԂ���Ȃ����̂Ƃ���B�܂��A���ėp���̃O���t�ł́A�ψʂƗ͂̒P�ʂ����ꂼ��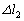 �C
�C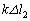 �Ƃ��ĕ\���Ă��邱�Ƃɒ��ӂ���B�܂��A�����I�ȓ_�̍��W�ɂ��ẮA���̐��l���O���t���ɋL������B
�Ƃ��ĕ\���Ă��邱�Ƃɒ��ӂ���B�܂��A�����I�ȓ_�̍��W�ɂ��ẮA���̐��l���O���t���ɋL������B
[C]�@������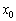 (
(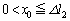 )�ŐÂ��ɕ������ꍇ�̏����̉^�����l����B
)�ŐÂ��ɕ������ꍇ�̏����̉^�����l����B (c) �����̉����x��a�Ƃ��ď����ɑ���^�����������A�^���̎���T�����߂�B�Ȃ��A�����xa�̕����́Ax���̌����Ɠ��l�ɉE�����𐳂Ƃ���B
[D]�@������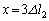 �ŐÂ��ɕ������ꍇ�̏����̉^���ɂ��Ĉȉ��̖₢�ɓ�����B�Ȃ��A�ȉ��̖₢�ł́A�K�v�ȏꍇ�ɂ́A
�ŐÂ��ɕ������ꍇ�̏����̉^���ɂ��Ĉȉ��̖₢�ɓ�����B�Ȃ��A�ȉ��̖₢�ł́A�K�v�ȏꍇ�ɂ́A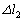 ��p���ĉ���B
��p���ĉ���B (d) ������x���̕��̗̈�ɂ���ꍇ�ɁA�ψʂ̐�Βl���ő�ƂȂ鏬���̍��W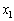 �����߂�B
�����߂�B (e) �ȏ�̍l�@�ɂ��ƂÂ��Ď��̕��͒��̇@����F���@�@�ɓ��Ă͂܂�K���Ȏ��A�܂��́A���l�����ɋL������B
������x�� �@ �̗̈�ł́Ax�� �A �𒆐S�Ƃ���U�� �B �Ŏ���T�� �C �̒P�U���̈ꕔ�ƂȂ�^��������B�܂��Ax�� �@ �̗̈�ł́Ax�� �D �𒆐S�Ƃ���U�� �E �C����T= �F �̒P�U���̈ꕔ�ƂȂ�^��������B�S�̂Ƃ��ė��҂��Ax�� �@ �Ŋ��炩�ɐڑ����ꂽ���̂ƂȂ�B
�y�L���z��������L���ł��B�����̊F���܂̂��x�������������肽���A��낵�����肢�������܂��B
�y�L���z�L���͂����܂łł��B
���@[A](a) �荇���̈ʒu�ŏ����ɓ������́Ax���������ɃS���Ђ�2������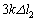 �Cx���������ɃS���Ђ�1������
�Cx���������ɃS���Ђ�1������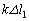 �C����2�����͂̂荇�����A
�C����2�����͂̂荇�����A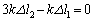 ����@
����@ �S���Ђ��������ɂ��āA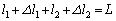 ����A
����A
�@���A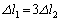 �C�A�ɑ�����āA
�C�A�ɑ�����āA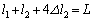
�� 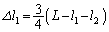 �C
�C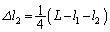 ......[��]
......[��] 
[B](b) 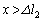 �ł́A�S���Ђ�2�͂���݂܂��B
�ł́A�S���Ђ�2�͂���݂܂��B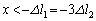 �ł́A�S���Ђ�1������݂܂��B�]���āA
�ł́A�S���Ђ�1������݂܂��B�]���āA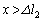 �C
�C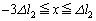 �C
�C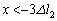 ��3�̗̈�ŕ����čl����K�v������܂��B
��3�̗̈�ŕ����čl����K�v������܂��B (i) 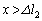 �̂Ƃ��A�S���Ђ�2�͂���݁A�S���Ђ�1���L����
�̂Ƃ��A�S���Ђ�2�͂���݁A�S���Ђ�1���L����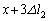 �ł��B����S���Ђ�2�������y�ڂ����B�S���Ђ�1��������x���������������܂��B����āA
�ł��B����S���Ђ�2�������y�ڂ����B�S���Ђ�1��������x���������������܂��B����āA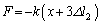
(ii) 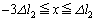 �̂Ƃ��A�S���Ђ�1�̐L�т�
�̂Ƃ��A�S���Ђ�1�̐L�т�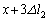 �C�S���Ђ�2���L����
�C�S���Ђ�2���L����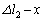 �ł��B�S���Ђ�1��������x���������A�S���Ђ�2��������x���������������܂��B����āA
�ł��B�S���Ђ�1��������x���������A�S���Ђ�2��������x���������������܂��B����āA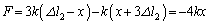
(iii) 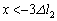 �̂Ƃ��A�S���Ђ�1�͂���݁A�S���Ђ�2���L����
�̂Ƃ��A�S���Ђ�1�͂���݁A�S���Ђ�2���L����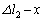 �ł��B�S���Ђ�2��������x���������������܂��B����āA
�ł��B�S���Ђ�2��������x���������������܂��B����āA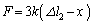
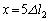 �̂Ƃ��A
�̂Ƃ��A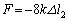 �C
�C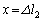 �̂Ƃ��A
�̂Ƃ��A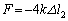 �C
�C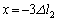 �̂Ƃ��A
�̂Ƃ��A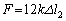 �C
�C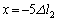 �̂Ƃ��A
�̂Ƃ��A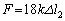
�ȏ���AF��x�̊W��\���O���t�͉E�}�B
[C](c) ������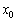 (
(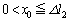 )�ŐÂ��ɕ������ꍇ�A����������ɂ����ẮA������
)�ŐÂ��ɕ������ꍇ�A����������ɂ����ẮA������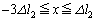 �̗̈�ɂ���̂ŁA[B](b)��(ii)���A�����ɂ�
�̗̈�ɂ���̂ŁA[B](b)��(ii)���A�����ɂ�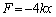 �Ƃ������������܂��B����āA�������^���������́A
�Ƃ������������܂��B����āA�������^���������́A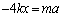
�� 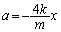 ����́A�p�U����
����́A�p�U����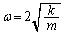 ���P�U����\���܂��B�U�����S��
���P�U����\���܂��B�U�����S��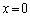 �ŁA
�ŁA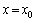 �ŕ����Ă���̂��U����
�ŕ����Ă���̂��U����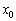 �ƂȂ�A
�ƂȂ�A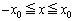 �͈̔͂��P�U�����܂��B���͈̔͂́A[B](b)(ii)�͈̔�
�͈̔͂��P�U�����܂��B���͈̔͂́A[B](b)(ii)�͈̔�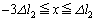 �Ɋ��S�Ɋ܂܂��̂ŁA���߂�^���������́A
�Ɋ��S�Ɋ܂܂��̂ŁA���߂�^���������́A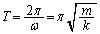 ......[��]
......[��]
[D](d) �������ʒu��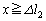 �ɂ���Ԃ́A[B](b)(i)���A�����ɓ�������
�ɂ���Ԃ́A[B](b)(i)���A�����ɓ�������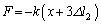 �ŁA�^���������́A
�ŁA�^���������́A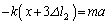
�� 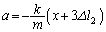 ����́A�p�U����
����́A�p�U����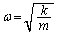 ���P�U����\���܂��B���̂Ƃ���������
���P�U����\���܂��B���̂Ƃ���������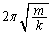 �ł��B�U�����S��
�ł��B�U�����S��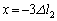 �ŁA
�ŁA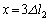 �ŕ����Ă���̂��U����
�ŕ����Ă���̂��U����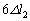 �ƂȂ�܂��B������x���������Ɍ������ē����Ă����ƁA
�ƂȂ�܂��B������x���������Ɍ������ē����Ă����ƁA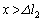 �͈̔͂���o�Ă��܂��܂��B
�͈̔͂���o�Ă��܂��܂��B
������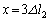 �ŐÂ��ɕ������Ƃ��A�ʒu�G�l���M�[
�ŐÂ��ɕ������Ƃ��A�ʒu�G�l���M�[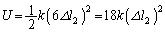 �������Ă��܂��B
�������Ă��܂��B
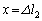 �܂ŗ����Ƃ��ɂ́A�S���Ђ�1���L����
�܂ŗ����Ƃ��ɂ́A�S���Ђ�1���L����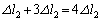 �ƂȂ�A�ʒu�G�l���M�[��
�ƂȂ�A�ʒu�G�l���M�[��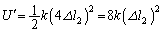
�]���āA���̂Ƃ����^���G�l���M�[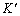 �́A�͊w�I�G�l���M�[�ۑ����A
�́A�͊w�I�G�l���M�[�ۑ����A �� 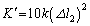
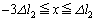 �͈̔͂ɂ����ẮA[C](c)�Ō����悤�ɁA�����́A
�͈̔͂ɂ����ẮA[C](c)�Ō����悤�ɁA�����́A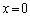 ���U�����S�Ƃ����p�U����
���U�����S�Ƃ����p�U����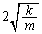 ���P�U�����s���܂��B������
���P�U�����s���܂��B������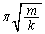 �ł��B
�ł��B
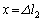 �ɗ����Ƃ����ʒu�G�l���M�[
�ɗ����Ƃ����ʒu�G�l���M�[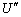 �́A[B](b)(ii)���˒萔��
�́A[B](b)(ii)���˒萔��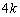 �ƍl���āA
�ƍl���āA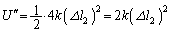 �ƂȂ�܂��B�^���G�l���M�[��
�ƂȂ�܂��B�^���G�l���M�[��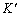 �̂܂ܕς��Ȃ��̂ŁA���̂Ƃ��S�͊w�I�G�l���M�[�́A
�̂܂ܕς��Ȃ��̂ŁA���̂Ƃ��S�͊w�I�G�l���M�[�́A ����������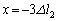 �܂ŗ����Ƃ���ƁA�ʒu�G�l���M�[��
�܂ŗ����Ƃ���ƁA�ʒu�G�l���M�[��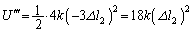 �ƂȂ�܂����A
�ƂȂ�܂����A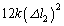 ���Ă��܂��̂ŁA������
���Ă��܂��̂ŁA������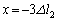 �ɓ��B�ł��܂���B
�ɓ��B�ł��܂���B
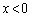 �ɂ������ψ��̐�Βl���ő�ƂȂ�Ƃ�(
�ɂ������ψ��̐�Βl���ő�ƂȂ�Ƃ�(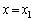 )���U�����S�����������
)���U�����S�����������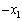 �ł��B���̂Ƃ����ʒu�G�l���M�[�́A
�ł��B���̂Ƃ����ʒu�G�l���M�[�́A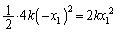 �C���̂Ƃ��^���G�l���M�[��0 (��u�Î~����)�Ȃ̂ŁA�͊w�I�G�l���M�[�ۑ����A
�C���̂Ƃ��^���G�l���M�[��0 (��u�Î~����)�Ȃ̂ŁA�͊w�I�G�l���M�[�ۑ����A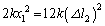
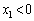 ���A
���A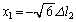 ......[��]�܂�A���̂Ƃ��̒P�U�����U����
......[��]�܂�A���̂Ƃ��̒P�U�����U����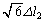 �ł��B
�ł��B
(e) ��L�̍l�@���A
�y�L���z��������L���ł��B�����̊F���܂̂��x�������������肽���A��낵�����肢�������܂��B
�y�L���z�L���͂����܂łł��B
�@�@���H�啨��TOP�@�@����TOP�@�@TOP�y�[�W�ɖ߂�
�y�L���z��������L���ł��B�����̊F���܂̂��x�������������肽���A��낵�����肢�������܂��B
�y�L���z�L���͂����܂łł��B
�e���̒��쌠��
�o���w�ɑ����܂��B©2005-2024(�L)����� ��w�y�w�m ���������t���I���n��w�l�b�g�m��w�y�w�m(���ē���������)������́A
�܂��A������܂Ń��[����
�����肭�������B