���啨��'02�N�O��[1]
 �@����L�̕s�����ȍׂ��p�C�v�̒��ɁA����m�̏���1�Ǝ���
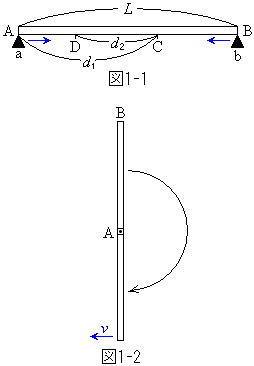
�@����L�̕s�����ȍׂ��p�C�v�̒��ɁA����m�̏���1�Ǝ���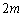 �̏���2�����ߍ��܂�Ă���B�p�C�v�͒�����ŋȂ��炸�A���̌��a�A�y�я����ȊO�̕����̎��ʂ͖����ł���قǏ������B�܂������͎��_�Ƃ݂Ȃ��Ă悢�Ƃ��A�d�͉����x��g�Ƃ���B�����̏����̈ʒu�ׂ邽�߂Ɏ��̓�̎������s�����B
�̏���2�����ߍ��܂�Ă���B�p�C�v�͒�����ŋȂ��炸�A���̌��a�A�y�я����ȊO�̕����̎��ʂ͖����ł���قǏ������B�܂������͎��_�Ƃ݂Ȃ��Ă悢�Ƃ��A�d�͉����x��g�Ƃ���B�����̏����̈ʒu�ׂ邽�߂Ɏ��̓�̎������s�����B
�T�@�܂��A�}1-1�Ɏ������悤�ɁA�p�C�v�̗��[A�CB���x�_a�Cb�Ő����Ɏx���A�����̎x�_���߂Â���悤�ȗ͂��������Ƃ����Ă������Ƃ���A�܂�b��C�̈ʒu�܂Ŋ����Ď~�܂�A���̒���ɍ��x��a������o����D�̈ʒu�Ŏ~�܂����B�p�C�v�Ǝx�_�̊Ԃ̐Î~���C�W���A�y�ѓ����C�W�������ꂼ��μ�C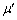 (������
(������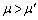 )�ƋL�����Ƃɂ��āA�ȉ��̖�ɓ�����B
)�ƋL�����Ƃɂ��āA�ȉ��̖�ɓ�����B (1) ����C�Ŏ~�܂钼�O�Ɏx�_a�Cb�ɂ������Ă���p�C�v�ɐ����ȕ����̗͂����ꂼ��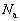 �C
�C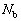 �Ƃ���B���̂Ƃ��̃p�C�v�ɉ����������̗͂̂荇����\�����������B
�Ƃ���B���̂Ƃ��̃p�C�v�ɉ����������̗͂̂荇����\�����������B (2) AC�̒����𑪒肵���Ƃ���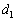 �ł������B�p�C�v�̏d�S�����[A����}����l�̈ʒu�ɂ���Ƃ���Ƃ��A�d�S�̎���̗͂̃��[�����g�̂荇�����l���邱�Ƃɂ��A
�ł������B�p�C�v�̏d�S�����[A����}����l�̈ʒu�ɂ���Ƃ���Ƃ��A�d�S�̎���̗͂̃��[�����g�̂荇�����l���邱�Ƃɂ��A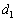 ��l�Cμ�C
��l�Cμ�C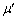 ��p���ĕ\���B
��p���ĕ\���B (3) CD�̒����𑪒肵���Ƃ���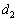 �ł������B���C�W���̔�
�ł������B���C�W���̔�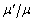 ��
��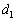 �C
�C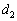 �ŕ\���B
�ŕ\���B (4) ��L�̑��肩��d�S�̈ʒul�����߂邱�Ƃ��ł���Bl��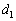 �C
�C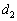 �ŕ\���B
�ŕ\���B (5) ����ɗ����̎x�_���߂Â���v���Z�X�𑱂���ƁA�ǂ̂悤�Ȍ��ۂ��N����A�ŏI�I�ɂǂ̂悤�ȏ�Ԃɍs���������A���R���܂߂ĊȒP�ɏq�ׂ�B
�U�@���ɁA�p�C�v�̒[A�ɏ����Ȍ����J���A�}1-2�̂悤�ɂ������x�_�Ƃ��ĉ����ɗ��Ă���Ԃ���Â��ɂ͂Ȃ��A�p�C�v����]�������B�p�C�v��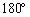 ��]�����Ƃ��̒[B�̑��x�̑傫���𑪂����Ƃ���Av�ł������B�[A����}��������1�C2�̈ʒu�����ꂼ��
��]�����Ƃ��̒[B�̑��x�̑傫���𑪂����Ƃ���Av�ł������B�[A����}��������1�C2�̈ʒu�����ꂼ��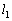 �C
�C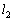 �Ƃ��Ĉȉ��̖�ɓ�����B(�x�_�ł̖��C����ы�C��R�͖����ł�����̂Ƃ���B)
�Ƃ��Ĉȉ��̖�ɓ�����B(�x�_�ł̖��C����ы�C��R�͖����ł�����̂Ƃ���B) (1) v��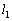 �C
�C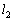 �Cg�CL��p���ĕ\���B
�Cg�CL��p���ĕ\���B (2) v�������T�œ���ꂽ�d�S�̈ʒul�̒l��p���ĕ\�����Ƃ���A
�@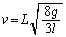
�y�L���z��������L���ł��B�����̊F���܂̂��x�������������肽���A��낵�����肢�������܂��B
�y�L���z�L���͂����܂łł��B
���@�������̏�ɏ����S���ł��u���āA2�{�̃{�[���y���ȂǂŎx���Ȃ���{�[���y���ɓ������ɗ͂������Ă݂Ă��������B���̖��̎������ȒP�ɍs�����Ƃ��ł��܂��B
������͂ǂ��ɉB����Ă���̂��A�T�����y���܂��Ă������ł�����܂��B
�T(1) �p�C�v�͐��������ɓ������A�x�_�������A�Ƃ������Ƃɒ��ӂ��Ă��������B�p�C�v�ɐ��������ɓ������́Aa�����E�������Î~���C����b����鍶�����������C��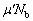 �ł��B����C�Ŏ~�܂钼�O�ɁA�p�C�v��a��������C���́Aa������o�����O�Ȃ̂ŁA�ő�Î~���C��
�ł��B����C�Ŏ~�܂钼�O�ɁA�p�C�v��a��������C���́Aa������o�����O�Ȃ̂ŁA�ő�Î~���C��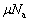 �ł��B����2�͂̂荇�����A
�ł��B����2�͂̂荇�����A 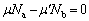 ......[��]�@����@
......[��]�@����@
(2) b���b�Ŏ~�܂钼�O�ɁA�p�C�v�ɉ��������ɓ������́Aa����������R��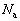 ��b����������R��
��b����������R��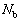 �ł��B�d�S��C�Ƃ�������
�ł��B�d�S��C�Ƃ�������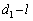 �ł��B
�ł��B 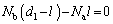 ����A
����A�@�C�A���A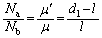
�� 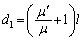 ......[��]�@����B
......[��]�@����B
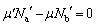 ����C
����C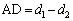
�d�S��D�Ƃ������́A
�d�S�̎�����͂̃��[�����g�̂荇�����A
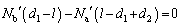 ����D
����D�C�C�D���A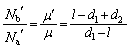
������ƁA �������ćB���g���ƁA
�� 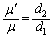 ......[��]�@����E
......[��]�@����E
(4) �E���B�ɑ������ƁA
�� 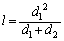 ......[��]
......[��]
(5) ����Ɏ����𑱂��āAB������o����E�Ŏ~�܂����Ƃ��܂��B���̂Ƃ��A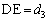 �Ƃ���ƁA
�Ƃ���ƁA �d�S��E�Ƃ������́A
(1)�C(2)�Ɠ��l�ɍl���āA�p�C�v�ɓ��������������͂̂荇���̎��ƁA�d�S�̎�����͂̃��[�����g�̂荇���̎��𗧂Ă�ƁA�p�C�v��a�Cb����������R����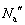 �C
�C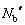 �Ƃ��āA
�Ƃ��āA 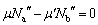 �@����F
�@����F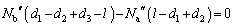
���̎��́A
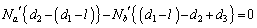 �@����G
�@����G�Ə��������ƁA�F�C�G�́A�C�C�D�ɂ����āAa��b�����ւ��A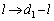 �C
�C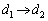 �C
�C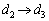 �Ƃ������̂ł��B�v�Z�����Ȃ��Ă��A
�Ƃ������̂ł��B�v�Z�����Ȃ��Ă��A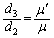 �ƂȂ邱�Ƃ��킩��܂��B�܂�A2�x�_�Ԃ�����
�ƂȂ邱�Ƃ��킩��܂��B�܂�A2�x�_�Ԃ�����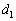 �C
�C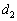 �C
�C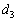 �C��� �́A����
�C��� �́A����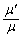 �����䐔���ɂȂ��Ă��āA
�����䐔���ɂȂ��Ă��āA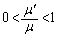 ���A�v���Z�X�����x���J��Ԃ��Ă����ƁA2�x�_�Ԃ������́A0�ɋ߂Â��Ă����܂��B2�x�_�́A�K���d�S�̗����ɂ���̂ŁA�ŏI�I��2�x�_���d�S�ɏd�Ȃ�܂��B
���A�v���Z�X�����x���J��Ԃ��Ă����ƁA2�x�_�Ԃ������́A0�ɋ߂Â��Ă����܂��B2�x�_�́A�K���d�S�̗����ɂ���̂ŁA�ŏI�I��2�x�_���d�S�ɏd�Ȃ�܂��B
�x�_a�Ǝx�_b������������������đ������~�܂�Ƃ������Ƃ��J��Ԃ��A���x�_�Ԃ̋����́A����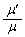 �̓��䐔��ƂȂ��ď������Ȃ�A
�̓��䐔��ƂȂ��ď������Ȃ�A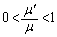 ���A0�ɋ߂Â��Ă����B�ŏI�I�ɁA���x�_�͏d�S�ɗ���B ......[��]
���A0�ɋ߂Â��Ă����B�ŏI�I�ɁA���x�_�͏d�S�ɗ���B ......[��]
���̘a���A�p�C�v��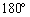 ��]�����Ƃ����^���G�l���M�[�ɂȂ�܂��B
��]�����Ƃ����^���G�l���M�[�ɂȂ�܂��B
�p�C�v��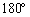 ��]�����Ƃ��́A����1�Ə���2�������͂��ꂼ��A
��]�����Ƃ��́A����1�Ə���2�������͂��ꂼ��A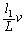 �C
�C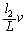 �ł�(�~�^���̌���
�ł�(�~�^���̌���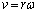 ���A�p���x��ω�Ƃ��āAB��������
���A�p���x��ω�Ƃ��āAB��������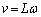 �C����1�C����2��������
�C����1�C����2��������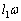 �C
�C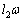 �C�Ȃ��A�����~�^�����Q��)�B�͊w�I�G�l���M�[�ۑ����A
�C�Ȃ��A�����~�^�����Q��)�B�͊w�I�G�l���M�[�ۑ����A �������āA
�� 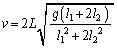 ......[��]
......[��]
(2) 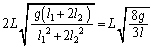
���ӂ�2�悵�Đ�������ƁA
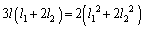 ����H
����H������A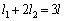
����ƁA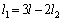 ���H�ɑ������ƁA
���H�ɑ������ƁA �������āA
�� 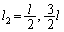
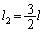 �̂Ƃ�
�̂Ƃ�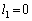 �ƂȂ��ĕs�K�B
�ƂȂ��ĕs�K�B
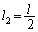 �̂Ƃ��A
�̂Ƃ��A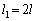
�� 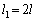 �C
�C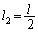 ......[��]
......[��]
�y�L���z��������L���ł��B�����̊F���܂̂��x�������������肽���A��낵�����肢�������܂��B
�y�L���z�L���͂����܂łł��B
�@�@���啨��TOP�@�@����TOP�@�@TOP�y�[�W�ɖ߂�
�y�L���z��������L���ł��B�����̊F���܂̂��x�������������肽���A��낵�����肢�������܂��B
�y�L���z�L���͂����܂łł��B
�e���̒��쌠��
�o���w�ɑ����܂��B©2005-2024(�L)����� ��w�y�w�m ���������t���I���n��w�l�b�g�m��w�y�w�m(���ē���������)������́A
�܂��A������܂Ń��[����
�����肭�������B