���啨��'03�N�O��[1]
 �@�}1�̂悤�ɁA����
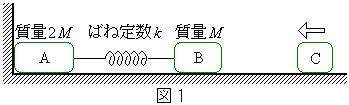
�@�}1�̂悤�ɁA����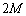 �̕���A�Ǝ���M�̕���B���A�˒萔k�̎��ʂ̖����ł���˂ɂ���ĂȂ���āA�Ȃ߂炩�Ő����ȏ��̏�ɐÎ~���Ă����B�܂��A����A�͂������ǂɐڂ��Ă����B���̏���������ɐi��ł�������C���A����B�Ɋ��S�e���Փ˂��āA���˕Ԃ��ꂽ�B�E�����𐳂̌����ƒ�߂�ƁA�Փ˒���̕���C�̑��x��
�̕���A�Ǝ���M�̕���B���A�˒萔k�̎��ʂ̖����ł���˂ɂ���ĂȂ���āA�Ȃ߂炩�Ő����ȏ��̏�ɐÎ~���Ă����B�܂��A����A�͂������ǂɐڂ��Ă����B���̏���������ɐi��ł�������C���A����B�Ɋ��S�e���Փ˂��āA���˕Ԃ��ꂽ�B�E�����𐳂̌����ƒ�߂�ƁA�Փ˒���̕���C�̑��x��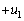 (
(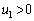 )�C����B�̑��x��
)�C����B�̑��x��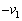 (
(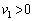 )�ł������B���̌�A����B�ƕ���C���ĂяՓ˂��邱�Ƃ͂Ȃ������B
)�ł������B���̌�A����B�ƕ���C���ĂяՓ˂��邱�Ƃ͂Ȃ������B
�T�@�܂��A�ՓˑO���畨��A���ǂ��痣���܂ł̉^�����l����B
(1) �ՓˑO�̕���C�̑��x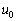 (
(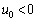 )��
)��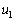 ��
��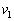 ��p���ĕ\���B
��p���ĕ\���B (2) �˂��ł��k�Ƃ��̎��R������̏k��x (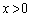 )�����߂�B
)�����߂�B (3) �Փ˂��Ă���˂̒��������R���ɖ߂�܂ł̎���T�����߂�B
�U�@�˂̒��������R���ɖ߂�ƁA���̒���ɕ���A���ǂ��痣�ꂽ�B
(1) �₪�āA�˂̒����͍ő�l�ɒB���A���̂Ƃ��̕���A�ƕ���B�̑��x�͓������Ȃ����B���̑��x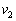 �����߂�B
�����߂�B (2) �˂̒������ő�l�ɒB�����Ƃ��̎��R������̐L��y (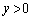 )�����߂�B
)�����߂�B (3) ���̌�˂��k��ŁA�������Ăю��R���ɖ߂����Ƃ��A����A�̑��x�͍ő�lV�ɒB�����BV�����߂�B
�V�@����A���ǂ��痣�ꂽ��A����B�ƕ���C�̊Ԋu�́A�˂��L�яk�݂��J��Ԃ����тɍL�����Ă������B���̂��Ƃ���킩��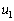 ��
��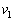 �̊W���A�s�����ŕ\���B
�̊W���A�s�����ŕ\���B
�y�L���z��������L���ł��B�����̊F���܂̂��x�������������肽���A��낵�����肢�������܂��B
�y�L���z�L���͂����܂łł��B
���@���������P�U���̖��ł́A�ɗ́A�^���������𗧂Ă��ɁA�G�l���M�[�I�l�@(�G�l���M�[�̌����A�͊w�I�G�l���M�[�ۑ���)�ōl����悤�ɂ��܂��傤�B�^���������ɗ���Ƃǂ����Ă����ϕ����o�Ă��āA�����ɂȂ�܂��B
�� 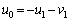 ......[��]
......[��] (2) �Փ˒����A+B���͊w�I�G�l���M�[�́A�^���G�l���M�[��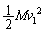 �̂݁B
�̂݁B �˂��ł��k�Ƃ�(A�CB�Ƃ����x0)��A+B���͊w�I�G�l���M�[�́A�e���G�l���M�[��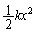 �̂݁B�͊w�I�G�l���M�[�ۑ����A
�̂݁B�͊w�I�G�l���M�[�ۑ����A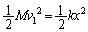
�� 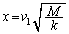 ......[��]
......[��] (3) ����B�̉^�����P�U���ŁA�����̍ő�l��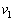 �C�U����
�C�U����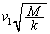 ((2)�ŋ��߂��ő���k�����U���ɂȂ�܂�)
((2)�ŋ��߂��ő���k�����U���ɂȂ�܂�) �P�U�����p�U������ω �Ƃ��āA�����F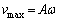 ���A
���A �� 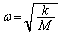 ���߂�����T�́A�P�U�����������ŁA
���߂�����T�́A�P�U�����������ŁA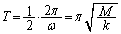 ......[��]
......[��]
�U�@�˂����R���ɖ߂�ƁA�˂�A�ɋy�ڂ�����0�C�]���āA�ǂ�A�ɋy�ڂ�����0�ɂȂ�A���̒���ɁAA�͕ǂ��痣��܂��B���̂Ƃ��AA�����x��0��B�����x��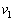 (C�Ƃ̏Փ˒���Ɠ���t����)�ł��B
(C�Ƃ̏Փ˒���Ɠ���t����)�ł��B (1) �˂̐L�т��ő�ɂȂ�Ƃ��AA���猩��B�͎~�܂�܂��B�Ƃ������Ƃ́A�����猩��ƁAA��B�����x�͓������x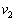 �ɂȂ�܂��B
�ɂȂ�܂��B �O������A��B�Ƃ˂���Ȃ�n�ɓ����Ă������͂���܂���B�]���āA�^���ʕۑ������������܂��BC�Ƃ̏Փ˒���AB�������^����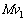 �������Ă��āA�˂��L�����ő�ɂȂ�Ƃ��AA�CB���^�����́A
�������Ă��āA�˂��L�����ő�ɂȂ�Ƃ��AA�CB���^�����́A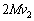 �C
�C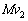 �ł��B�^���ʕۑ����A
�ł��B�^���ʕۑ����A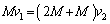
�� 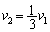 ......[��]
......[��]
(2) C �Ƃ̏Փˌ�ŏ��ɂ˂����R���ɖ߂�Ƃ��AB�������^���G�l���M�[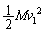 �������Ă��āAA���^���G�l���M�[�Ƃ˂��e���G�l���M�[��0�ł��B
�������Ă��āAA���^���G�l���M�[�Ƃ˂��e���G�l���M�[��0�ł��B �˂��������ő�ɂȂ����Ƃ��AA���^���G�l���M�[�́A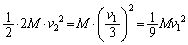 �CB���^���G�l���M�[�́A
�CB���^���G�l���M�[�́A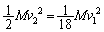 �C���̂Ƃ��̂˂��L����y�Ȃ̂ŁA�˂��e���G�l���M�[�́A
�C���̂Ƃ��̂˂��L����y�Ȃ̂ŁA�˂��e���G�l���M�[�́A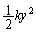
���̌n�ɑ����d�������Ă������͑��݂��Ȃ��̂ŁA�͊w�I�G�l���M�[�ۑ�����A �� 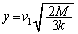 ......[��]
......[��]
(3) �˂����R���ɖ߂����Ƃ���B�����x��v�Ƃ��āA
�V�@A�CB����̂ƍl���āA�d�S�����x��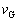 �Ƃ���(�^���ʕۑ����A�d�S�͓����x�^�������܂�)�ƁA
�Ƃ���(�^���ʕۑ����A�d�S�͓����x�^�������܂�)�ƁA 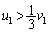 ......[��]
......[��]�ł���悢���ƂɂȂ�܂��B
�y�L���z��������L���ł��B�����̊F���܂̂��x�������������肽���A��낵�����肢�������܂��B
�y�L���z�L���͂����܂łł��B
�@�@���啨��TOP�@�@����TOP�@�@TOP�y�[�W�ɖ߂�
�y�L���z��������L���ł��B�����̊F���܂̂��x�������������肽���A��낵�����肢�������܂��B
�y�L���z�L���͂����܂łł��B
�e���̒��쌠��
�o���w�ɑ����܂��B©2005-2024(�L)����� ��w�y�w�m ���������t���I���n��w�l�b�g�m��w�y�w�m(���ē���������)������́A
�܂��A������܂Ń��[����
�����肭�������B