���啨��'04�N�O��[1]
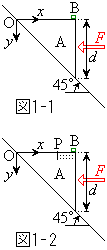 �}1-1�̂悤�ɐ����ɑ���
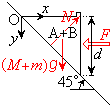
�}1-1�̂悤�ɐ����ɑ���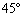 �̊p���Ȃ��Ζʏ�Ɏ���M�̒��p�ӎO�p�`�̕���A���Εӂ̖ʂ��ΖʂƐڂ���悤�ɒu���B���p�ӎO�p�`�̓�����2�ӂ̒�����d�Ƃ���BA�̏�ʂɎ���m�ő傫���̖����ł��鏬���ȕ���B��u���B�Ζʏ�Ɍ��_O���Ƃ�A�����E������x���A������������y�����Ƃ�B�͂��߁AA�͏�ʂ�
�̊p���Ȃ��Ζʏ�Ɏ���M�̒��p�ӎO�p�`�̕���A���Εӂ̖ʂ��ΖʂƐڂ���悤�ɒu���B���p�ӎO�p�`�̓�����2�ӂ̒�����d�Ƃ���BA�̏�ʂɎ���m�ő傫���̖����ł��鏬���ȕ���B��u���B�Ζʏ�Ɍ��_O���Ƃ�A�����E������x���A������������y�����Ƃ�B�͂��߁AA�͏�ʂ� �ƂȂ�ʒu�ɂ���AB��A�̏�ʂ̉E�[�A���Ȃ킿�A
�ƂȂ�ʒu�ɂ���AB��A�̏�ʂ̉E�[�A���Ȃ킿�A �̈ʒu�ɂ���B��C�̒�R����юΖʂ�A�̊Ԃ̖��C�͖����ł�����̂Ƃ���B�d�͉����x��g�Ƃ���B
�̈ʒu�ɂ���B��C�̒�R����юΖʂ�A�̊Ԃ̖��C�͖����ł�����̂Ƃ���B�d�͉����x��g�Ƃ���B
�T�@A��B�̊Ԃ̖��C�������ł���ꍇ�Ɉȉ��̖�ɓ�����B
(1) �}1-1�̂悤��A�̉E�ʂɐ����������ɗ�F���������Ƃ���A2�̕��͍̂ŏ��̈ʒu�ɐÎ~�����܂܂ł������BF�̑傫�������߂�B
(2) ��F����菜�����Ƃ���AA��B�͉^�����J�n�����B���̌�AB��A��ʂ̍��[�ɒB�����B���̏u�Ԃ�B��y���W�����߂�B
(3) B��A��ʂ̍��[�ɒB���钼�O��B�̑���v�����߂�B
�U�@�}1-2�Ɏ����悤��A��ʂ̓_P�����ɂ��ĉE���̕\�ʂ��e���A���̕����ł�A��B�̊Ԃ̐Î~���C�W������ѓ����C�W���͂��ꂼ��μ�C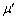 (�������A
(�������A )�ł���BA��ʂ̓_P��荶���́A�Ȃ߂炩�Ȃ܂܂ł���B��T(1)�Ɠ��l�ɁA��F�������ė����̂�Î~�������B��F����菜������̗����̂̉^���ɂ��Ĉȉ��̖�ɓ�����B
)�ł���BA��ʂ̓_P��荶���́A�Ȃ߂炩�Ȃ܂܂ł���B��T(1)�Ɠ��l�ɁA��F�������ė����̂�Î~�������B��F����菜������̗����̂̉^���ɂ��Ĉȉ��̖�ɓ�����B 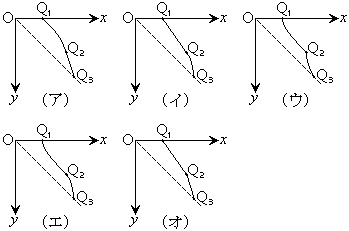 (1) μ���\���ɑ傫���ꍇ�AB��A��ʂ�����o�����A�����͈̂�̂ƂȂ��ĎΖʂ����肨���B���̂Ƃ��̗����̂�x�����̉����x
(1) μ���\���ɑ傫���ꍇ�AB��A��ʂ�����o�����A�����͈̂�̂ƂȂ��ĎΖʂ����肨���B���̂Ƃ��̗����̂�x�����̉����x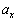 ��y�����̉����x
��y�����̉����x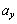 �����߂�B
�����߂�B(2) μ������l ���傫�����B��A��ʂ�����o�����A��������Ί���o���B���̒l
���傫�����B��A��ʂ�����o�����A��������Ί���o���B���̒l �����߂�B
�����߂�B
�y�L���z��������L���ł��B�����̊F���܂̂��x�������������肽���A��낵�����肢�������܂��B
�y�L���z�L���͂����܂łł��B
���@�ȒP�ȏݒ�ł����A�������蕨���I�ɍl�@����K�v������܂��B
�T(1) �@�E�}�̂悤�ɁAA�{B����̂Ƃ��čl���܂��B�Î~�����܂܂Ȃ̂ŁAA�{B�ɓ����͂̂荇���̎��𗧂Ă܂��B ���������F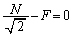
���������F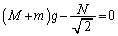
�� 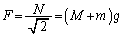 ......[��]
......[��]
(2) B�ɓ������̐���������0�ł��BB�������x�̐���������0�ł��B����āAB�͐��������ɂ͓������A�^���Ɍ������ĉ^�����܂��B
A��ʂ̍��[�ɒB�����Ƃ���B��y���W��d ......[��]
(3) A�CB�Ԃ������R����AB�Ԃ�B�̉^�������Ɛ����ɓ��������d�������܂���B�Ζʂ�A�̊Ԃ������R�����d�������܂���B�]���āAA�{B�ɂ��ė͊w�I�G�l���M�[�ۑ������������܂��B
A�CB�Ƃ����������x�^������̂ŁA���҂������x�̑傫����A�Ca�C(1)��(2)��������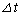 �Ƃ��܂��B
�Ƃ��܂��B 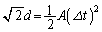 �C
�C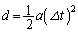
�� 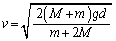 �@......[��]
�@......[��]
�U(1) �Ζʂɉ��������ɓ������́A�d���̎Ζʂɉ��������̐����F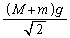 �ł��B
�ł��B A+B�̎Ζʂɉ��������������x��a�Ƃ��āA�Ζʂɉ����������^���������F �� 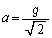 ��
�� 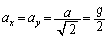 ......[��]
......[��]
���������F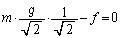 �C���������F
�C���������F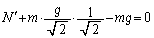
������A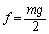 �C
�C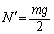
����o�����E�ł��Î~���C�����ő�Î~���C���ɓ������A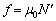 ���A
���A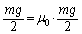
�� 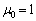 ......[��]
......[��]
(3) 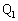 ��
��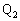 �ł�B�͐��������ɂ����������ɂ��������x�^�����܂��B
�ł�B�͐��������ɂ����������ɂ��������x�^�����܂��B B�̐��������A���������������x������a�Cb�Ƃ��āA
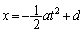 �C
�C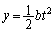
������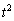 ���������āA
���������āA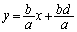 �C���̃O���t�͒����ł��B
�C���̃O���t�͒����ł��B
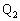 ��
��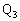 �ł́A�����������������x�^��(�����x�̑傫����
�ł́A�����������������x�^��(�����x�̑傫����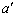 �Ƃ��܂�)�Ő��������������x�^���ɂȂ�܂��BB��
�Ƃ��܂�)�Ő��������������x�^���ɂȂ�܂��BB��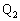 �ɒB����������
�ɒB����������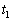 �C
�C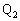 �ɂ�����B�����x�̐��������A����������
�ɂ�����B�����x�̐��������A����������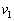 �C
�C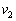 �C
�C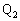 �̍��W��
�̍��W��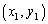 �Ƃ��āAB�̈ʒu
�Ƃ��āAB�̈ʒu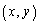 �́A
�́A ������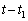 ���������āA
���������āA
�y�L���z��������L���ł��B�����̊F���܂̂��x�������������肽���A��낵�����肢�������܂��B
�y�L���z�L���͂����܂łł��B
�@�@���啨��TOP�@�@����TOP�@�@TOP�y�[�W�ɖ߂�
�y�L���z��������L���ł��B�����̊F���܂̂��x�������������肽���A��낵�����肢�������܂��B
�y�L���z�L���͂����܂łł��B
�e���̒��쌠��
�o���w�ɑ����܂��B©2005-2024(�L)����� ��w�y�w�m ���������t���I���n��w�l�b�g�m��w�y�w�m(���ē���������)������́A
�܂��A������܂Ń��[����
�����肭�������B