���啨��'04�N�O��[3]
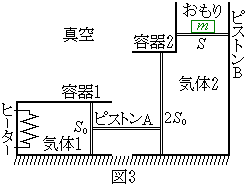 �@�}3�̂悤�ɁA��̗e��1�C2�̂��ꂼ���1�����̋C��1�C2�����A�����ȏ��ɌŒ肷��B�����̋C�̂͂Ƃ��ɗ��z�C�̂Ƃ���B��̗e��͖��C�Ȃ��ɐ����ɓ������Ƃ̂ł���s�X�g��A�łȂ���Ă���B�s�X�g��A�̗e��1���̒�ʐς�
�@�}3�̂悤�ɁA��̗e��1�C2�̂��ꂼ���1�����̋C��1�C2�����A�����ȏ��ɌŒ肷��B�����̋C�̂͂Ƃ��ɗ��z�C�̂Ƃ���B��̗e��͖��C�Ȃ��ɐ����ɓ������Ƃ̂ł���s�X�g��A�łȂ���Ă���B�s�X�g��A�̗e��1���̒�ʐς�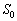 �ł���A�e��2���̒�ʐς�
�ł���A�e��2���̒�ʐς�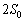 �ł���B�e��2�ɂ͂���ɁA�㉺�ɓ������Ƃ̂ł���s�X�g��B�����Ă���A���̏�Ɏ���m�̂����肪�̂��Ă���B�s�X�g��B�̒�ʐς�S�ł���A���̎��ʂ͖����ł���B�e��1�ɂ͑̐ς̖����ł���q�[�^�[�����t�����Ă���B�s�X�g��A�CB�Ɨe��͔M��ʂ��Ȃ��B�C�̂͗e��̊O�ɂ��ꂸ�A�e��̊O�͐^��ł���B�C�̒萔��R�C�d�͉����x��g�Ƃ���B
�ł���B�e��2�ɂ͂���ɁA�㉺�ɓ������Ƃ̂ł���s�X�g��B�����Ă���A���̏�Ɏ���m�̂����肪�̂��Ă���B�s�X�g��B�̒�ʐς�S�ł���A���̎��ʂ͖����ł���B�e��1�ɂ͑̐ς̖����ł���q�[�^�[�����t�����Ă���B�s�X�g��A�CB�Ɨe��͔M��ʂ��Ȃ��B�C�̂͗e��̊O�ɂ��ꂸ�A�e��̊O�͐^��ł���B�C�̒萔��R�C�d�͉����x��g�Ƃ���B
�T�@�s�X�g��B�������Ȃ��悤�ɌŒ肳��Ă���ꍇ���l����B
(1) �s�X�g��A���Î~���Ă����Ԃɂ����āA�C��1�̈���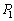 �ƋC��2�̈���
�ƋC��2�̈���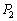 �̊Ԃɐ��藧�W���������B
�̊Ԃɐ��藧�W���������B (2) �͂��ߋC��1�̕����C��2��艷�x���Ⴍ�A�C��1�̑̐ς�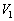 �C�C��2�̑̐ς�
�C�C��2�̑̐ς�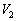 �ł������B�q�[�^�[�ŋC��1�����M���ċC��1�C2�������x�ɂ����B���̂Ƃ��̋C��2�̑̐�
�ł������B�q�[�^�[�ŋC��1�����M���ċC��1�C2�������x�ɂ����B���̂Ƃ��̋C��2�̑̐�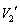 ���A
���A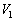 �C
�C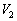 ��p���ĕ\���B
��p���ĕ\���B �U�@�s�X�g��B�����C�Ȃ��������Ƃ��ł���ꍇ���l����B�s�X�g��A�CB���Î~���Ă����Ԃɂ����āA�C��1�̉��x��T�ł���Ƃ��A�C��1�̑̐�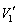 ���AS�CT�CR�Cm�Cg��p���ĕ\���B
���AS�CT�CR�Cm�Cg��p���ĕ\���B �V�@��U�̏�Ԃ���C�̇T���q�[�^�[�ʼn��M�����Ƃ���A�C��1�̉��x��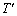 �ɂȂ�A�C��2�̉��x�͕ς��Ȃ������B�܂��A�s�X�g��A�͉E�ɋ���x�����������ƈړ����A�s�X�g��B��h�����㏸�����B
�ɂȂ�A�C��2�̉��x�͕ς��Ȃ������B�܂��A�s�X�g��A�͉E�ɋ���x�����������ƈړ����A�s�X�g��B��h�����㏸�����B (1) �ړ�����x���A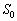 �CS�Ch��p���ĕ\���B
�CS�Ch��p���ĕ\���B (2) ���x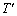 ���AT�CR�Cm�Cg�Ch��p���ĕ\���B
���AT�CR�Cm�Cg�Ch��p���ĕ\���B (3) �C��1�͒P���q���z�C�̂Ƃ��āA�q�[�^�[���������ꂽ�M��Q���Am�Cg�Ch��p���ĕ\���B
�y�L���z��������L���ł��B�����̊F���܂̂��x�������������肽���A��낵�����肢�������܂��B
�y�L���z�L���͂����܂łł��B
���@���啨���ł悭������A�������̏������ǂ���̑I�����Ďg���čs�����A�Ƃ����Ƃ���ɓ����g�����ł��B�C�̖̂��Ƃ��Ă͓��ł͂���܂���B�Ȃ��A���z�C�����Q�Ƃ��Ă��������B
�T(1) �C��1�C�C��2��������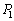 �C
�C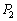 �Ƃ��܂��B
�Ƃ��܂��B �s�X�g��A�́A�C��1����E��������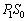 ���A�C��2���獶��������
���A�C��2���獶��������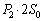 ���܂��B
���܂��B
�s�X�g��A�ɓ����͂̂荇���F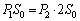
�� 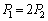 ......[��]
......[��]
(2) ��ԕ������Ɨ͂̂荇�����l���邾���ł͏������s�����܂��B��蕶�̐�̕���ǂ�ł݂�ƁA�V�Ńs�X�g��A���E������x�����A�Ƃ����L�q������܂��B�s�X�g�����ړ������ɒ��ڂ��Ă݂܂��B
�C��1�����M�����Ƃ��A�s�X�g��A���E(�C��1�͉��x�㏸���Ă��邩��c������)��x�����Ƃ��܂��B�C��1���̐���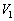 ����
����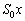 ��������
��������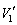 �ɂȂ�A�C��2���̐���
�ɂȂ�A�C��2���̐���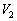 ����
����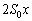 ��������
��������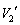 �ɂȂ����Ƃ��܂��B
�ɂȂ����Ƃ��܂��B ���M��̋C��1��������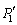 �C�C��1�ƋC��2����Ή��x��T�Ƃ��āA
�C�C��1�ƋC��2����Ή��x��T�Ƃ��āA
�C��1����ԕ������F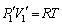 ����A�C�C��2�̏�ԕ������F
����A�C�C��2�̏�ԕ������F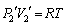 ����B
����B
�܂��A�s�X�g��A�ɓ����͂̂荇�����A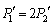 ����C
����C
�A�C�B�C�C���A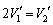
������@�ɑ������ƁA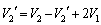 �@��
�@�� 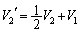 ......[��]
......[��]
�U�@�����ł��A�s�X�g��A�ɓ����͂̂荇������A�C��1�ƋC��2������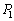 �C
�C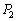 �̊ԂɁA
�̊ԂɁA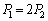 �Ƃ����W���������܂��B
�Ƃ����W���������܂��B �s�X�g��B�ɓ����͂̂荇���F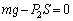
�� 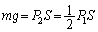 ��
�� 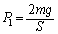 �C��1�̏�ԕ������F
�C��1�̏�ԕ������F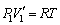 ����D
����D
�� 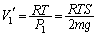 ......[��]
......[��]
�V�@�]���̎��M������l�łȂ�����A�����������́A�͂��߂�����ɂ�낤�Ƃ���Ǝ��s���܂��B��̒����Ƃ��돇�X�ɍU�߂Ă����܂��B
�܂��C��2���l���܂��B�C��2�́A���x���ς��Ȃ��̂������G�l���M�[�͕ω����܂����B
�C��2�ł��M�̂��Ƃ���Ȃ��̂ŁA�M�͊w���@�����A�s�X�g��A���炳�ꂽ�d���͂��̂܂܃s�X�g��B�������グ���d���ɂȂ�܂��B
�Ƃ������Ƃ́A�C��2�̏�Ԃ͉����ω����Ȃ��Ƃ������Ƃł��B�܂�A�C��
2�������A�̐��́A���l�A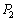 �C
�C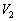 �̂܂܂ƍl�����܂��B
�̂܂܂ƍl�����܂��B
����ɁA�s�X�g��A�ɓ����͂̂荇�����A�C��1�������͈��ŁA�C��1���舳�ω������Ă������Ƃ��킩��܂��B
(1) �C��2���̐��ɂ��āF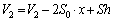
�� 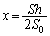 ......[��]
......[��]
(2) (1)�̌��ʂ�p����ƁA���M��̋C��1���̐��́A
�C��1��������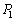 �Ƃ��āA���M��̋C��1�̏�ԕ������F
�Ƃ��āA���M��̋C��1�̏�ԕ������F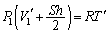 ����E
����E
�E���D���A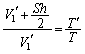 (�V�������̖@��)��
(�V�������̖@��)�� 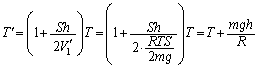 ......[��]
......[��] (3) �C��1���舳�ω������Ă���̂ŁA�舳������M�̎��𗘗p���܂�(������M���Q��)�B �P���q���q���z�C�̂ł́A��σ�����M��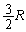 �C�舳������M��
�C�舳������M��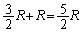 �ł��B
�ł��B
�C��1�ɂ��āA�舳������M�̎��ɂ��A�q�[�^�[���������ꂽ�M��Q�́A 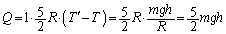 ......[��]
......[��]
�y�L���z��������L���ł��B�����̊F���܂̂��x�������������肽���A��낵�����肢�������܂��B
�y�L���z�L���͂����܂łł��B
�@�@���啨��TOP�@�@����TOP�@�@TOP�y�[�W�ɖ߂�
�y�L���z��������L���ł��B�����̊F���܂̂��x�������������肽���A��낵�����肢�������܂��B
�y�L���z�L���͂����܂łł��B
�e���̒��쌠��
�o���w�ɑ����܂��B©2005-2024(�L)����� ��w�y�w�m ���������t���I���n��w�l�b�g�m��w�y�w�m(���ē���������)������́A
�܂��A������܂Ń��[����
�����肭�������B