東大物理'18年前期[2]
真空中に置かれた、ばねを組み込んだ平行板コンデンサーに関する以下の設問に答えよ。ただし、真空の誘電率を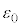 とし、ばね自身の誘電率による電気容量の変化は無視できるとする。また、金属板は十分に広く端の効果は無視できるものとし、金属板間の電荷の移動は十分に速くその移動にかかる時間も無視できるものとする。さらに、金属板の振動による電磁波の発生、および重力の影響も無視できるとする。
とし、ばね自身の誘電率による電気容量の変化は無視できるとする。また、金属板は十分に広く端の効果は無視できるものとし、金属板間の電荷の移動は十分に速くその移動にかかる時間も無視できるものとする。さらに、金属板の振動による電磁波の発生、および重力の影響も無視できるとする。
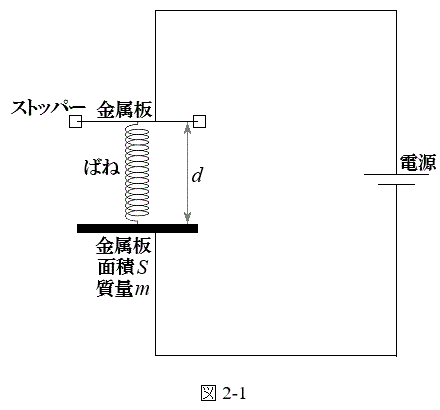 Ⅰ 図2-1のように、同じ面積Sの2枚の金属板からなる平行板コンデンサーが電源につながれている。2枚の金属板は、ばね定数kの絶縁体のばねでつながれており、上の金属板はストッパーで固定されている。下の金属板は質量mをもち、上の金属板と平行のまま上下に移動し、上の金属板との間隔を変化させることができる。
Ⅰ 図2-1のように、同じ面積Sの2枚の金属板からなる平行板コンデンサーが電源につながれている。2枚の金属板は、ばね定数kの絶縁体のばねでつながれており、上の金属板はストッパーで固定されている。下の金属板は質量mをもち、上の金属板と平行のまま上下に移動し、上の金属板との間隔を変化させることができる。電源の電圧をVにしたところ、ばねは自然長からわずかに縮み、金属板の間隔がdとなる位置で静電気力とばねの弾性力がつりあい、下の金属板は静止した。
(1) 金属板間にはたらいている静電気力の大きさを求めよ。
(2) ばねに蓄えられている弾性エネルギーを求めよ。
(3) この状態から、下の金属板を引っ張り、上の金属板との間隔をdから までわずかに広げて放すと、下の金属板はつりあいの位置を中心に単振動した。この単振動の周期を求めよ。ただし、
までわずかに広げて放すと、下の金属板はつりあいの位置を中心に単振動した。この単振動の周期を求めよ。ただし、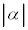 が1より十分小さい実数αに対して成り立つ近似式、
が1より十分小さい実数αに対して成り立つ近似式、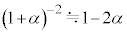 を用いてよい。
を用いてよい。 [補足説明] Ⅰ(3)において、電源の電圧はVで一定に保たれている。
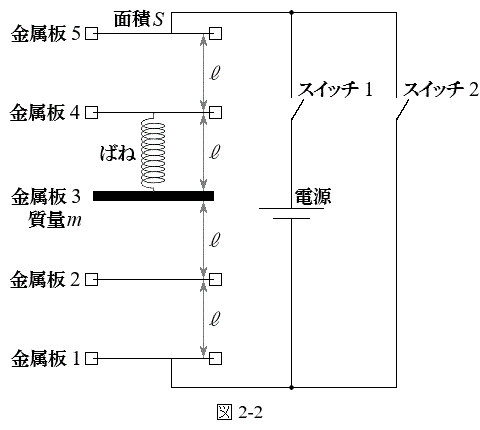 Ⅱ 図2-2のような同じ面積Sの5枚の金属板からなる平行板コンデンサーを含む回路を考える。金属板1,2,4,5は固定されている。質量mをもつ金属板3は、金属板4にばね定数kのばねでつながれており、ほかの金属板と平行のまま、上下に移動することができる。金属板2,3,4には、それぞれ、
Ⅱ 図2-2のような同じ面積Sの5枚の金属板からなる平行板コンデンサーを含む回路を考える。金属板1,2,4,5は固定されている。質量mをもつ金属板3は、金属板4にばね定数kのばねでつながれており、ほかの金属板と平行のまま、上下に移動することができる。金属板2,3,4には、それぞれ、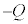 ,
,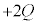 ,
,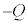 の電荷が与えられている。金属板1と5は、図2-2に示すような電源と二つのスイッチを含んだ回路に接続されている。はじめ、スイッチ1は閉じ、スイッチ2は開いており、電源の電圧は0であった。このとき、5枚の金属板は静止しており、隣り合った金属板の間隔はすべて
の電荷が与えられている。金属板1と5は、図2-2に示すような電源と二つのスイッチを含んだ回路に接続されている。はじめ、スイッチ1は閉じ、スイッチ2は開いており、電源の電圧は0であった。このとき、5枚の金属板は静止しており、隣り合った金属板の間隔はすべて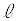 で、ばねは自然長になっていた。
で、ばねは自然長になっていた。まず、電源の電圧を0から小さな値V (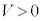 )までゆっくり変化させた。この過程で金属板3はつねに力のつり合いを保ちながら移動し、金属板1と金属板5にはそれぞれ
)までゆっくり変化させた。この過程で金属板3はつねに力のつり合いを保ちながら移動し、金属板1と金属板5にはそれぞれ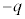 ,
,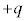 の電荷が蓄えられた。
の電荷が蓄えられた。 (1) このとき、金属板3の元の位置からの変位xを、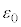 ,Q,q,k,Sを用いて表せ。ただし、図2-2中の下向きをxの正の向きとする。
,Q,q,k,Sを用いて表せ。ただし、図2-2中の下向きをxの正の向きとする。 (2) このときの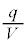 を全電気容量と呼ぶ。
を全電気容量と呼ぶ。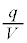 を、
を、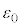 ,Q,k,S,
,Q,k,S, を用いて表せ。
を用いて表せ。 (3) 次にスイッチ1を開きスイッチ2を閉じると金属板3は単振動した。この運動において、金属板3の図2-2の位置からの変位がxのときの金属板5の電荷を、Q,x,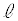 を用いて表せ。ただし、図2-2中の下向きをxの正の向きとする。
を用いて表せ。ただし、図2-2中の下向きをxの正の向きとする。 (4) 設問Ⅱ(3)の単振動の周期を求めよ。
[補足説明] Ⅱにおいて、ばね定数kは十分に大きいものとする。
【広告】ここから広告です。ご覧の皆さまのご支援ご理解を賜りたく、よろしくお願いいたします。
【広告】広告はここまでです。
解答 難問とは言えませんが、煩雑で面倒な計算を強いられる問題です。
Ⅰ(1) 2枚の金属板間にできているコンデンサーの静電容量は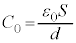 ,金属板間に電圧Vがかかっているので、コンデンサーが蓄える電気量Qは、
,金属板間に電圧Vがかかっているので、コンデンサーが蓄える電気量Qは、 金属板間の距離はdなので、金属板間に生ずる電場の強さは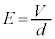
金属板間に働く静電気力の大きさFは、公式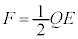 より、
より、 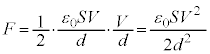 ......[答] (下の金属板に働く力の向きは図の上向き)
......[答] (下の金属板に働く力の向きは図の上向き)
(2) ばねの自然長からの縮みを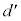 とすると、ばねの弾性力
とすると、ばねの弾性力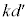 と(1)のFとのつり合いより、
と(1)のFとのつり合いより、 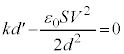 ∴
∴ 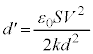 ・・・①
・・・①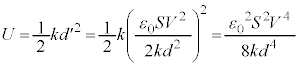 ......[答]
......[答]
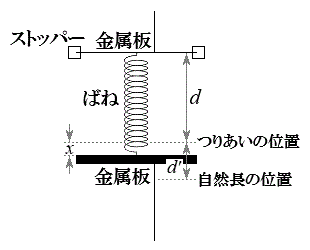 (3) 右図のように、下の金属板がつり合いの位置からxだけ下がった状況を考えると、2枚の金属板間の距離は
(3) 右図のように、下の金属板がつり合いの位置からxだけ下がった状況を考えると、2枚の金属板間の距離は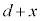 ,ばねの自然長からの縮みは
,ばねの自然長からの縮みは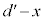 です。金属板間の静電気力
です。金属板間の静電気力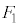 は、(1)の結果で、
は、(1)の結果で、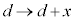 とし、問題文の近似式を用いて、
とし、問題文の近似式を用いて、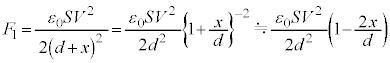 (図で上向き)
(図で上向き)ばねの弾性力は図の下向きで、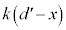 xを下向き正になるようにとったので、下の金属板の下向きの加速度をaとして、運動方程式は、
xを下向き正になるようにとったので、下の金属板の下向きの加速度をaとして、運動方程式は、 ①より、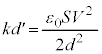 ,よって、
,よって、 これは、角振動数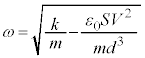 の単振動を表します。単振動の周期Tは、
の単振動を表します。単振動の周期Tは、 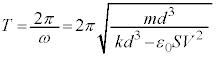 ......[答]
......[答]
Ⅱ 金属板5の電荷を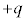 とすると、金属板4の上側の電荷は
とすると、金属板4の上側の電荷は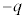 です。金属板4の全電荷は
です。金属板4の全電荷は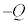 なので、金属板4の下側の電荷は
なので、金属板4の下側の電荷は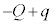 です。金属板3の上側の電荷は
です。金属板3の上側の電荷は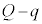 ,金属板3の全電荷は
,金属板3の全電荷は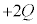 なので、金属板3の下側の電荷は
なので、金属板3の下側の電荷は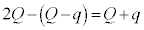 です。金属板2の上側の電荷は
です。金属板2の上側の電荷は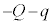 です。金属板2の全電荷は
です。金属板2の全電荷は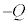 なので、金属板2の下側の電荷は
なので、金属板2の下側の電荷は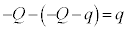 です。よって、
です。よって、 金属板5と金属板4の間のコンデンサーが蓄えている電気量はq (金属板5が高電位),
金属板4と金属板3の間のコンデンサーが蓄えている電気量は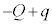 ,
, 金属板3と金属板2の間のコンデンサーが蓄えている電気量は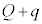 ,
, 金属板2と金属板1の間のコンデンサーが蓄えている電気量はq (金属板2が高電位),
となります。
(1) 金属板3と金属板4の間(極板間距離は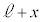 ,静電容量は
,静電容量は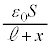 ,電圧は
,電圧は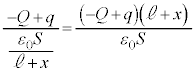 ,電場の強さは
,電場の強さは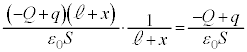 )に働く静電気力
)に働く静電気力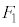 (引力なので向きは図の上向き)はⅠ(1)と同様にして、
(引力なので向きは図の上向き)はⅠ(1)と同様にして、 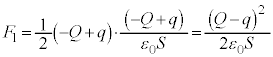 ・・・②
・・・②金属板2と金属板3の間(極板間距離は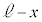 ,静電容量は
,静電容量は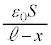 ,電圧は
,電圧は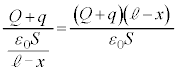 ,電場の強さは
,電場の強さは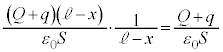 )に働く静電気力
)に働く静電気力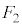 (引力なので向きは図の下向き)は、
(引力なので向きは図の下向き)は、  ・・・③
・・・③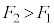 なので、変位xは正でばねは伸びており、ばねの弾性力
なので、変位xは正でばねは伸びており、ばねの弾性力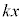 は上向きです。よって、力のつり合いより、
は上向きです。よって、力のつり合いより、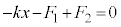
∴ 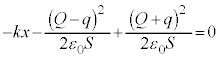 ,
,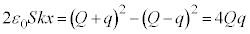
∴ 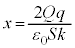 ......[答]
......[答]
(2) 金属板5と金属板4の間のコンデンサーの静電容量、金属板2と金属板1の間のコンデンサーの静電容量は、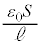 で、ともに電荷qを蓄えているので電圧は
で、ともに電荷qを蓄えているので電圧は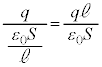 です。キルヒホッフ第2法則より、各コンデンサーの電圧の和はVなので、②,③より、
です。キルヒホッフ第2法則より、各コンデンサーの電圧の和はVなので、②,③より、 (1)の結果を代入すると、
∴ 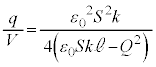 ......[答]
......[答]
(3) スイッチ2を閉じると、金属板5と金属板1は等電位になります。④で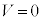 とすると、
とすると、 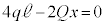 ∴
∴ 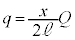 ......[答]
......[答]
(4) (3)の結果を②,③に代入することにより、変位がxのときに金属板3に働く静電気力は、
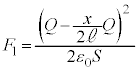 ,
,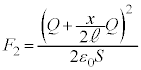 ・・・⑤
・・・⑤金属板3には、その他にばねの弾性力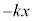 が働きます。
が働きます。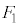 が上向き、
が上向き、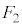 が下向きであることに注意し、また、下向きを正としているので、
が下向きであることに注意し、また、下向きを正としているので、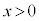 のとき、弾性力は
のとき、弾性力は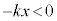 (弾性力は上向き)であることに注意すると、金属板の運動方程式は、加速度をaとして、
(弾性力は上向き)であることに注意すると、金属板の運動方程式は、加速度をaとして、 ⑤を代入し、
∴ 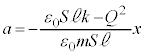 これは、角振動数
これは、角振動数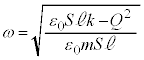 の単振動を表します。周期Tは、
の単振動を表します。周期Tは、 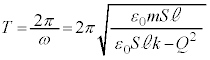 ......[答]
......[答]
【広告】ここから広告です。ご覧の皆さまのご支援ご理解を賜りたく、よろしくお願いいたします。
【広告】広告はここまでです。
東大物理TOP 物理TOP TOPページに戻る
【広告】ここから広告です。ご覧の皆さまのご支援ご理解を賜りたく、よろしくお願いいたします。
【広告】広告はここまでです。
各問題の著作権は
出題大学に属します。©2005-2025(有)りるらる 苦学楽学塾 随時入会受付中!理系大学受験ネット塾苦学楽学塾(ご案内はこちら)ご入会は、
まず、こちらまでメールを
お送りください。 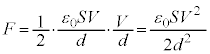 ......[答] (下の金属板に働く力の向きは図の上向き)
......[答] (下の金属板に働く力の向きは図の上向き)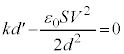 ∴
∴ 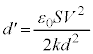 ・・・①
・・・①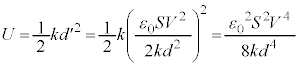 ......[答]
......[答]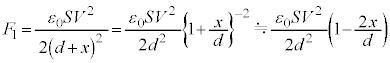 (図で上向き)
(図で上向き)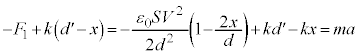
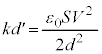 ,よって、
,よって、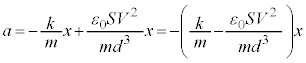
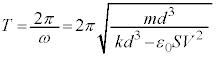 ......[答]
......[答]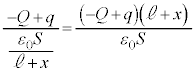 ,電場の強さは
,電場の強さは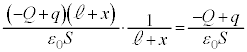 )に働く静電気力
)に働く静電気力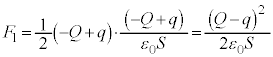 ・・・②
・・・②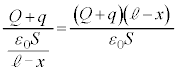 ,電場の強さは
,電場の強さは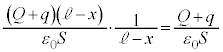 )に働く静電気力
)に働く静電気力 ・・・③
・・・③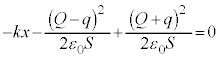 ,
,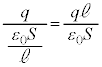 です。キルヒホッフ第2法則より、各コンデンサーの電圧の和はVなので、②,③より、
です。キルヒホッフ第2法則より、各コンデンサーの電圧の和はVなので、②,③より、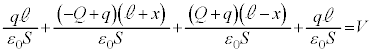

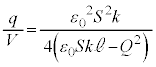 ......[答]
......[答]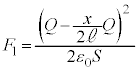 ,
,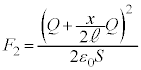 ・・・⑤
・・・⑤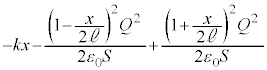
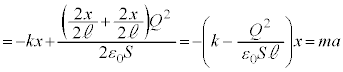
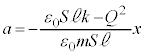
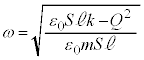 の単振動を表します。周期Tは、
の単振動を表します。周期Tは、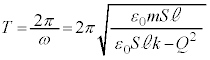 ......[答]
......[答]