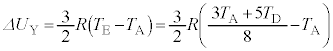���啨��'20�N�O��[3]
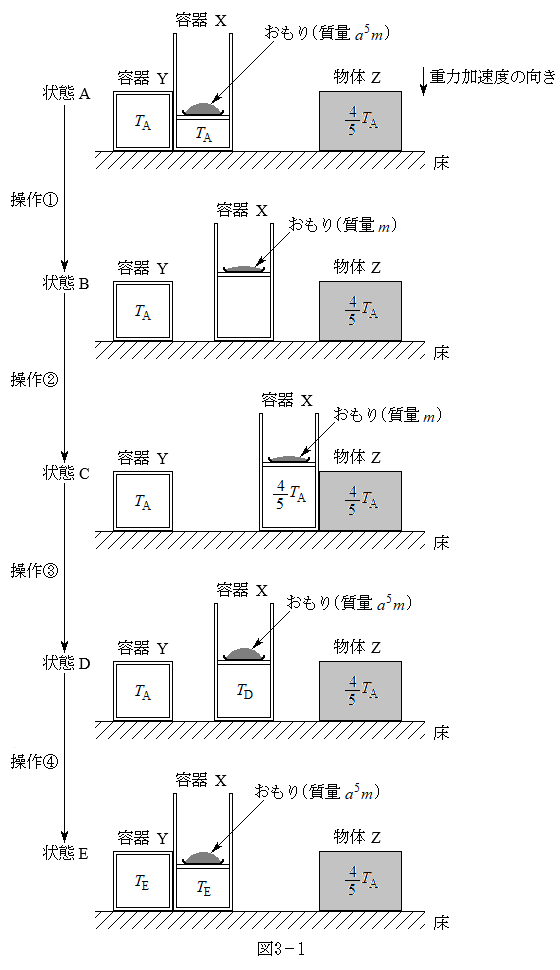 �}3�|1�Ɏ����悤�ɁA�e��X�CY�ɂ��ꂼ��1�����̒P���q���q���z�C�̂������Ă���B�e��X�̏㕔�͊��炩�ɓ����s�X�g���ŕ����Ă���A�s�X�g���̏�ɂ͂����肪�ڂ����Ă���B�s�X�g���̎��ʂ͖����ł���B�e��Y�̑̐ς͈��ł���B�e��̊O�͐^��ł���A�e��X�ƁA�e��Y�܂��͕���Z���ڐG�����ꍇ�ɂ̂ݔM�̂��Ƃ肪�s���A�O���̐^��⏰�ȂǂƂ̔M�̂��Ƃ�͏�ɖ����ł�����̂Ƃ���B�e��̔M�e�ʂ͖����ł���B�܂��A����Z�̉��x�͏��
�}3�|1�Ɏ����悤�ɁA�e��X�CY�ɂ��ꂼ��1�����̒P���q���q���z�C�̂������Ă���B�e��X�̏㕔�͊��炩�ɓ����s�X�g���ŕ����Ă���A�s�X�g���̏�ɂ͂����肪�ڂ����Ă���B�s�X�g���̎��ʂ͖����ł���B�e��Y�̑̐ς͈��ł���B�e��̊O�͐^��ł���A�e��X�ƁA�e��Y�܂��͕���Z���ڐG�����ꍇ�ɂ̂ݔM�̂��Ƃ肪�s���A�O���̐^��⏰�ȂǂƂ̔M�̂��Ƃ�͏�ɖ����ł�����̂Ƃ���B�e��̔M�e�ʂ͖����ł���B�܂��A����Z�̉��x�͏�� �ɕۂ���Ă�����̂Ƃ���B
�ɕۂ���Ă�����̂Ƃ���B
�͂��߁A�e��X�͗e��Y�ƐڐG���Ă���A�s�X�g���̏�ɂ͎��� (
(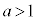 )�̂����肪�ڂ����Ă���B�e��X���̋C�̂̈��͂�
)�̂����肪�ڂ����Ă���B�e��X���̋C�̂̈��͂�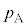 �ł���B�e��X�CY���̋C�̂̉��x�͂Ƃ���
�ł���B�e��X�CY���̋C�̂̉��x�͂Ƃ���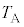 �ł���B���̂Ƃ��̗e��X���̋C�̂̏�Ԃ����A�ƌĂԂ��Ƃɂ���B�����āA�}3�|1�Ɏ����悤�ɁA�ȉ��̑���@�`�C�����Ԃɍs���A�e��X���̋C�̂̏�Ԃ��AA��B��C��D��E�ƕω��������B�����̑���ɂ����āA�C�̂̏�ԕω��͂������ƋN������̂Ƃ���B�C�̒萔��R�Ƃ���ƁA���A�`D�ɂ�����e��X���̋C�̂̈��́A���x�A�̐ρA�����G�l���M�[�͕\3�|1�̂悤�ɗ^������B
�ł���B���̂Ƃ��̗e��X���̋C�̂̏�Ԃ����A�ƌĂԂ��Ƃɂ���B�����āA�}3�|1�Ɏ����悤�ɁA�ȉ��̑���@�`�C�����Ԃɍs���A�e��X���̋C�̂̏�Ԃ��AA��B��C��D��E�ƕω��������B�����̑���ɂ����āA�C�̂̏�ԕω��͂������ƋN������̂Ƃ���B�C�̒萔��R�Ƃ���ƁA���A�`D�ɂ�����e��X���̋C�̂̈��́A���x�A�̐ρA�����G�l���M�[�͕\3�|1�̂悤�ɗ^������B
����@(A��B)�@�e��X���A�e��Y�C����Z�̂�����Ƃ��ڐG���Ȃ��ʒu�Ɉړ��������B���ɁA�s�X�g����̂���������ʂ�m�ɂȂ�܂ŏ��X�Ɍ��炵���B
����A(B��C)�@�e��X��Z�ɐڐG�����A�e��X���̋C�̂̉��x��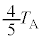 �ɂȂ�܂ŕ��u�����B
�ɂȂ�܂ŕ��u�����B
����B(C��D)�@�e��X���A�e��Y�C����Z�̂�����Ƃ��ڐG���Ȃ��ʒu�Ɉړ��������B���ɁA�s�X�g����̂���������ʂ�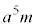 �ɂȂ�܂ŏ��X�ɑ��₵���B
�ɂȂ�܂ŏ��X�ɑ��₵���B ���̑����̗e��X���̋C�̂̉��x��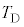 �Ƃ���B
�Ƃ���B
����C(D��E)�@�e��X��e��Y�ƐڐG�����A�e��X�CY���̋C�̂̉��x���������Ȃ�܂ŕ��u�����B���̂Ƃ��̉��x��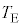 �Ƃ���B
�Ƃ���B
�ȉ��̐ݖ�ɓ�����B
�T�@����@�`�B�ɂ����āA�e��X���̋C�̂����ꂽ�d�������ꂼ��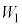 �C
�C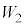 �C
�C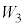 �Ƃ���B
�Ƃ���B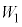 �C
�C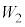 �C
�C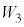 ��R�C
��R�C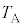 �Ca��p���ĕ\���B
�Ca��p���ĕ\���B
�U�@����C�ɂ��e��X���̋C�̂̏�ԕω�(D��E)�ɂ��āA�ȉ��̐ݖ�ɓ�����B
(1) ����C�ɂ��e��X���̋C�̂̓����G�l���M�[�̕ω�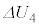 ���AR�C
���AR�C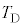 �C
�C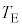 ��p���ĕ\���B
��p���ĕ\���B (2) ����C�ɂ����āA�e��X���̋C�̂����ꂽ�d��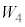 ���AR�C
���AR�C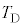 �C
�C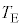 ��p���ĕ\���B(3) ���E�ɂ�����e��X���̋C�̂̉��x
��p���ĕ\���B(3) ���E�ɂ�����e��X���̋C�̂̉��x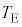 ���A
���A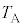 �C
�C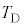 ��p���ĕ\���B
��p���ĕ\���B
�@�@�@�@�@�@�@�@�\3�|1
| ���� | ���x | �̐� | �����G�l���M�[ |
| ���A | 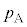 | 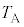 | 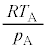 | 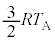 |
| ���B | 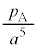 | 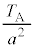 | 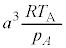 | 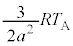 |
| ���C | 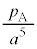 | 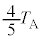 | 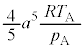 |  |
| ���D | 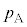 | 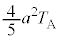 ( (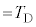 ) ) | 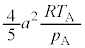 | 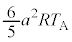 |
 �V�@a�̒l��������������Ƃ��A����@�`�C�́A�e��X���̋C�̂ɑ��Ďd�����s�����ƂŁA�ቷ�̕���Z����e��Y���̍����̋C�̂ɔM���^�ԑ���ɂȂ��Ă���B����C�ɂ��e��Y���̋C�̂̓����G�l���M�[�̕ω���
�V�@a�̒l��������������Ƃ��A����@�`�C�́A�e��X���̋C�̂ɑ��Ďd�����s�����ƂŁA�ቷ�̕���Z����e��Y���̍����̋C�̂ɔM���^�ԑ���ɂȂ��Ă���B����C�ɂ��e��Y���̋C�̂̓����G�l���M�[�̕ω���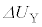 �Ƃ��āA�ȉ��̐ݖ�ɓ�����B
�Ƃ��āA�ȉ��̐ݖ�ɓ�����B
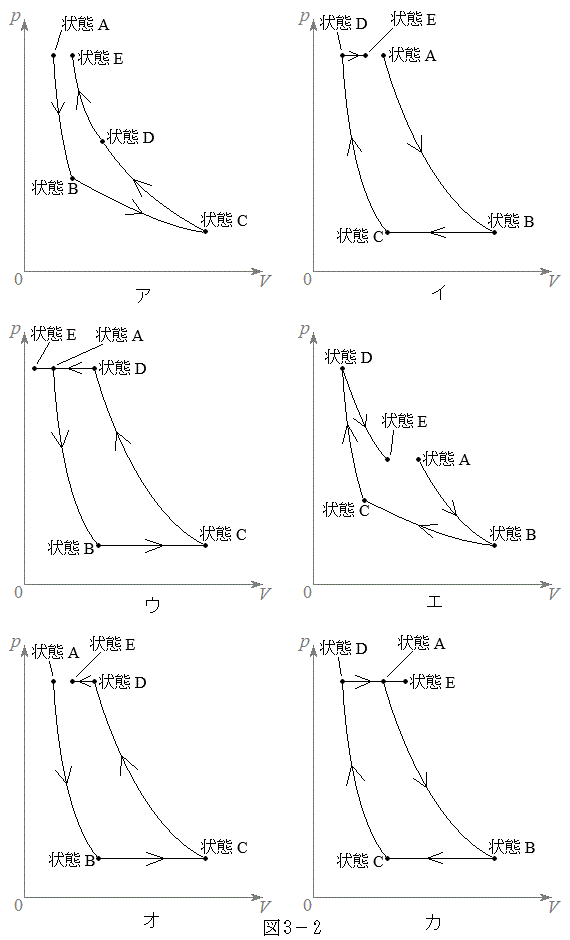
(1) ����C�ɂ���ėe��Y���̋C�̂̓����G�l���M�[����������(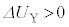 )�Ƃ��A����@�`�C�ɂ�����e��X���̋C�̂̈���p�Ƒ̐�V�̊W��\���}�Ƃ��čł��K�Ȃ��̂��A�}3�|2�̃A�`�J�̒������I��œ�����B
)�Ƃ��A����@�`�C�ɂ�����e��X���̋C�̂̈���p�Ƒ̐�V�̊W��\���}�Ƃ��čł��K�Ȃ��̂��A�}3�|2�̃A�`�J�̒������I��œ�����B
(2) 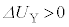 �ƂȂ邽�߂�a�Ɋւ����������B
�ƂȂ邽�߂�a�Ɋւ����������B
(3) ����@�`�C�̊Ԃɗe��X���̋C�̂����ꂽ�d���̑��a��W�C����A�ɂ����ėe��X���̋C�̂�����Z������M�ʂ�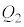 �Ƃ���B
�Ƃ���B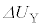 ���AW��
���AW��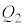 ��p���ĕ\���B
��p���ĕ\���B
(4) ���E���炳��Ɉ��������A����@�`�C�����x���J��Ԃ��ƁA�e��Y���̋C�̂̉��x�́A���鉷�x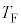 �ɑQ�߂���B
�ɑQ�߂���B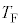 ���A
���A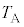 ��a��p���ĕ\���B
��a��p���ĕ\���B
�y�L���z��������L���ł��B�����̊F���܂̂��x�������������肽���A��낵�����肢�������܂��B
�y�L���z�L���͂����܂łł��B
���@��ԕ������𗧂Ă��Ƃ��A�e��Ԃ̈��́A���x�A�̐ρA�����G�l���M�[���\3�|1�ɗ^�����Ă��āA���ԕs���ɂȂ�Ȃ��悤�ɔz������Ă��܂��B
�T�@�e��X���̋C�̂̕ω����l���܂��B����@�ł͔M�̂��Ƃ肪�Ȃ��̂��f�M�ω��ł��B����A�ł͂�����ɂ��d�͂ɕω����Ȃ����͂��ς�炸�舳�ω��ł��B����B�ł͔M�̂��Ƃ肪�Ȃ��f�M�ω��ł��B����C�͑���A�Ɠ��l�ɒ舳�ω��ł��B�ȉ��A�\3�|1�̃f�[�^���g���ċ��߂܂��B
����@�ł͒f�M�ω��Ȃ̂ŁA�M�͊w���@���ɂ��A�C�̂����ꂽ�d���͋C�̂̓����G�l���M�[�̑����ɓ������Ȃ�܂��B����āA 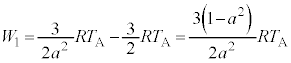 ......[��]
......[��]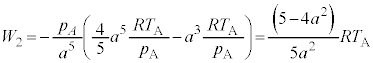 ......[��]
......[��]����B�ł͒f�M�ω��Ȃ̂ŁA�M�͊w���@���ɂ��A�C�̂����ꂽ�d���͋C�̂̓����G�l���M�[�̑����ɓ������A
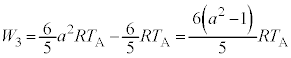 ......[��]
......[��]
�U(1) ����C�ł́A�e��X����1�����̋C�̂̉��x��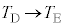 �ƕω�����̂ŁA�����G�l���M�[�̕ω�
�ƕω�����̂ŁA�����G�l���M�[�̕ω�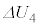 �́A
�́A 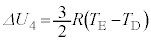 ......[��]
......[��]
(2) ����C�͒舳�ω��Ȃ̂ŁA�舳������M�̎����A�e��X���̋C�̂��z�������M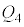 �́A
�́A 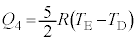 �@���(A)
�@���(A) ......[��]
......[��]
(3) (A)�̔M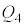 �́A����C�ŗe��Y���̋C�̂��^�����M�ɓ������Ȃ�܂��B�e��Y���̋C�̂���ϕω����A�e��Y����1�����̋C�̂��^�����M�́A���x��
�́A����C�ŗe��Y���̋C�̂��^�����M�ɓ������Ȃ�܂��B�e��Y���̋C�̂���ϕω����A�e��Y����1�����̋C�̂��^�����M�́A���x��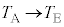 �ƕω�����̂ŁA��σ�����M�̎����A
�ƕω�����̂ŁA��σ�����M�̎����A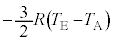 �@(�^�����M�Ȃ̂Ń}�C�i�X����)
�@(�^�����M�Ȃ̂Ń}�C�i�X����) 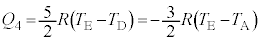 ��
�� 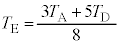 ......[��]
......[��]
�V�@����C�ɂ��e��Y����1�����̋C�̂̓����G�l���M�[�̕ω�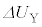 �́A���x��
�́A���x��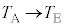 �ƕω�����̂ŁA�U(3)�̌��ʂ�p���āA
�ƕω�����̂ŁA�U(3)�̌��ʂ�p���āA 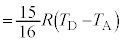 �@���(B)
�@���(B)(1) 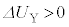 �C(B)���A
�C(B)���A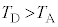 �ł��B
�ł��B �U(3)�̌��ʂ��A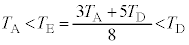 �@(
�@(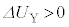 �Ȃ̂ŁA�e��Y���̋C�̂́A����C�̊Ԃɉ��x���㏸��
�Ȃ̂ŁA�e��Y���̋C�̂́A����C�̊Ԃɉ��x���㏸��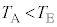 �ł�)�����ŁA�A�C�C���舳�ω��̃C�A�E�A�I�A�J�̂����ꂩ�ŁA���̂����A���x���A
�ł�)�����ŁA�A�C�C���舳�ω��̃C�A�E�A�I�A�J�̂����ꂩ�ŁA���̂����A���x���A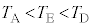 �̊W�ɂ���(�舳�ω��̃O���t��ŁA������E�ցA���A�C���E�C���D�̏��ɕ���)���̂́A�I ......[��]
�̊W�ɂ���(�舳�ω��̃O���t��ŁA������E�ցA���A�C���E�C���D�̏��ɕ���)���̂́A�I ......[��]
(2) (1)�̌���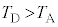 ���A�\3�|1�̃f�[�^��p���āA
���A�\3�|1�̃f�[�^��p���āA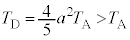
�� 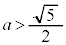 ......[��]
......[��]
(3) ����C�̊ԁA�e��Y���̋C�̂͒�ϕω�����̂ŁA�M�͊w���@�����A�e��Y���̋C�̂��z�������M�́A�����G�l���M�[�̑�����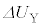 �ɓ������A�e��X���̋C�̂��e��Y����z�������M��
�ɓ������A�e��X���̋C�̂��e��Y����z�������M��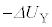 �ł�(�����ɒ���)�B
�ł�(�����ɒ���)�B ����@�ƇB�͒f�M�ω��Ȃ̂ŁA����@�`�C�̊Ԃɗe��X���̋C�̂��z�������M�́A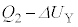 �C�����G�l���M�[�̑������́A���x��
�C�����G�l���M�[�̑������́A���x��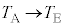 �ƕω����邱�Ƃ���A
�ƕω����邱�Ƃ���A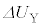 �ɓ������Ȃ�܂��B
�ɓ������Ȃ�܂��B
����āA�M�͊w���@�����A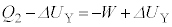
�� 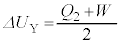 ......[��]
......[��]
(4) ����@�`�C��n��J��Ԃ�����̗e��Y���̋C�̂̉��x��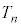 �Ƃ���ƁA�U��(3)�̌��ʂɂ����āA
�Ƃ���ƁA�U��(3)�̌��ʂɂ����āA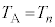 �C
�C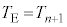 �Ƃ��āA
�Ƃ��āA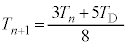
�e��Y���̋C�̂̉��x��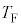 �ɑQ�߂����Ƃ��A
�ɑQ�߂����Ƃ��A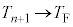 �C
�C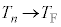 �Ƃ��āA
�Ƃ��āA 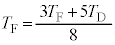 �@���@
�@���@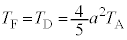 ......[��]�@(�����ł�2���ԑQ�����������K�v�͂���܂���)
......[��]�@(�����ł�2���ԑQ�����������K�v�͂���܂���)
�y�L���z��������L���ł��B�����̊F���܂̂��x�������������肽���A��낵�����肢�������܂��B
�y�L���z�L���͂����܂łł��B
�@�@���啨��TOP�@�@����TOP�@�@TOP�y�[�W�ɖ߂�
�y�L���z��������L���ł��B�����̊F���܂̂��x�������������肽���A��낵�����肢�������܂��B
�y�L���z�L���͂����܂łł��B
�e���̒��쌠��
�o���w�ɑ����܂��B©2005-2024(�L)����� ��w�y�w�m ���������t���I���n��w�l�b�g�m��w�y�w�m(���ē���������)������́A
�܂��A������܂Ń��[����
�����肭�������B 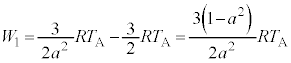 ......[��]
......[��]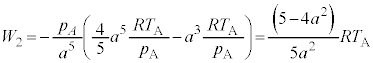 ......[��]
......[��]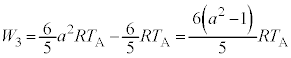 ......[��]
......[��]