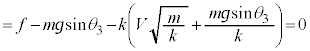東大物理'24年前期[1]
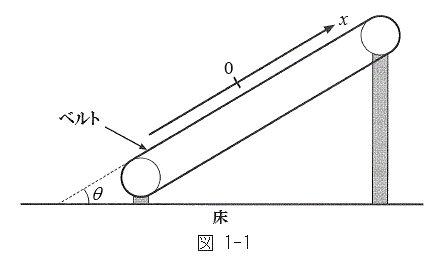 図1-1のように、十分に長いベルトをもつベルトコンベアをベルトと床とのなす角がθ (
図1-1のように、十分に長いベルトをもつベルトコンベアをベルトと床とのなす角がθ (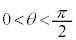 )となるように水平な床に固定する。ベルトのなす斜面に沿ったx軸を斜面上向きが正になるようにとる。x軸は常に床に対して静止している。このベルト上の物体の運動を考える。物体Aの質量はmである。また、ベルトと物体Aとの間の静止摩擦係数はμ,動摩擦係数は
)となるように水平な床に固定する。ベルトのなす斜面に沿ったx軸を斜面上向きが正になるようにとる。x軸は常に床に対して静止している。このベルト上の物体の運動を考える。物体Aの質量はmである。また、ベルトと物体Aとの間の静止摩擦係数はμ,動摩擦係数は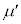 である。物体はx軸方向にのみ運動し、回転しないものとする。特に断りの無い限り、物体の座標や速度はこのx軸に対して定義する。重力加速度を
である。物体はx軸方向にのみ運動し、回転しないものとする。特に断りの無い限り、物体の座標や速度はこのx軸に対して定義する。重力加速度を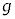 とし、物体の大きさや空気抵抗は無視してよい。
とし、物体の大きさや空気抵抗は無視してよい。
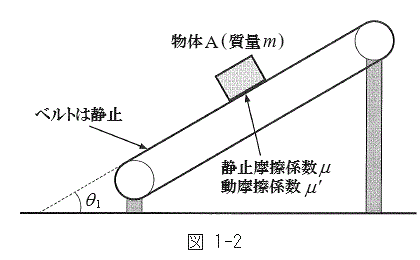 Ⅰ はじめに図1-2のように、
Ⅰ はじめに図1-2のように、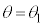 とし、ベルトが静止しているときの物体Aの運動を考える。
とし、ベルトが静止しているときの物体Aの運動を考える。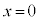 において物体Aに初速度
において物体Aに初速度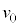 (
(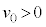 )を与えたところ、物体Aは斜面に沿って上昇した後、再び
)を与えたところ、物体Aは斜面に沿って上昇した後、再び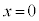 に戻った。
に戻った。(1) 物体Aが最高点に到達したときのx座標を求めよ。
(2) 物体Aが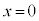 に戻ったときの速度を
に戻ったときの速度を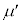 ,
,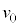 ,
,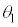 ,m,
,m,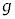 のうち必要なものを用いて表せ。
のうち必要なものを用いて表せ。
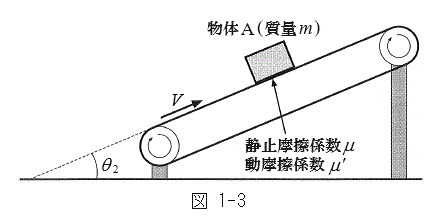 Ⅱ 次に、図1-3のように
Ⅱ 次に、図1-3のように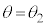 とし、一定の速度V (
とし、一定の速度V (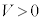 )でベルトが動いているときの物体Aの運動を考える。
)でベルトが動いているときの物体Aの運動を考える。
(1) 時刻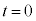 に物体Aを初速度0でベルトにおいたところ、物体Aは斜面上向きに移動し始めた。物体Aの速度を時刻t (
に物体Aを初速度0でベルトにおいたところ、物体Aは斜面上向きに移動し始めた。物体Aの速度を時刻t (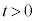 )の関数として表せ。
)の関数として表せ。
(2) 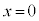 において物体Aに初速度
において物体Aに初速度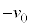 (
(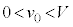 )を与えたところ、物体Aは斜面に沿って下降した後、再び
)を与えたところ、物体Aは斜面に沿って下降した後、再び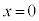 に戻った。物体Aが
に戻った。物体Aが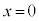 に戻ったときの速度を求めよ。
に戻ったときの速度を求めよ。
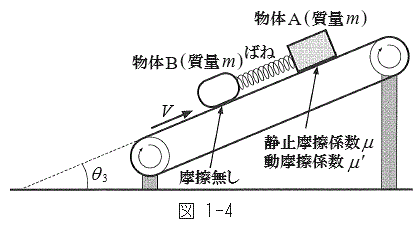 Ⅲ 図1-4のように
Ⅲ 図1-4のように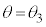 とし、ばね定数kのばねでつながれた物体Aと物体Bをベルト上におく。物体Aは物体Bより常に高い位置にある。ベルトは一定の速度V (
とし、ばね定数kのばねでつながれた物体Aと物体Bをベルト上におく。物体Aは物体Bより常に高い位置にある。ベルトは一定の速度V (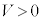 )で動いている。物体Bの質量はmで、物体Bとベルトとの間に摩擦はない。ばねは均質であり、ばねの質量は無視できる。
)で動いている。物体Bの質量はmで、物体Bとベルトとの間に摩擦はない。ばねは均質であり、ばねの質量は無視できる。ばねを自然長から長さ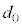 だけ伸ばした状態で、物体Aおよび物体Bを速度0でベルトにおいたところ、二つの物体はx軸に対して静止し続けた。
だけ伸ばした状態で、物体Aおよび物体Bを速度0でベルトにおいたところ、二つの物体はx軸に対して静止し続けた。
(1) 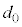 をV,
をV,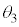 ,m,
,m,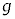 ,kのうち必要なものを用いて表せ。
,kのうち必要なものを用いて表せ。
(2) 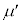 をV,
をV,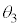 ,m,
,m,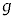 ,kのうち必要なものを用いて表せ。
,kのうち必要なものを用いて表せ。 次に物体Bの速度を0からVに瞬間的に変えた。この時刻を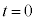 とする。物体Aは時刻
とする。物体Aは時刻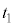 (
(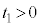 )にはじめてベルトと同じ速度になった。物体Aおよび物体Bの速度をそれぞれ
)にはじめてベルトと同じ速度になった。物体Aおよび物体Bの速度をそれぞれ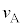 および
および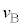 とする。
とする。
(3) 時刻t (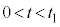 )における物体Aと物体Bの重心Gの速度
)における物体Aと物体Bの重心Gの速度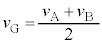 をt,V,
をt,V,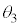 ,m,
,m,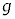 ,kのうち必要なものを用いて表せ。
,kのうち必要なものを用いて表せ。
(4) 時刻t (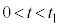 )における物体Aおよび物体Bの運動は、重心Gから見るとそれぞれ単振動とみなせる。このことを用いて
)における物体Aおよび物体Bの運動は、重心Gから見るとそれぞれ単振動とみなせる。このことを用いて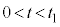 における
における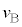 および
および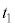 を、それぞれt,V,
を、それぞれt,V,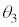 ,m,
,m,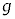 ,kのうち必要なものを用いて表せ。ここで、重心Gから物体Aおよび物体Bまでの距離がともにdだけ減少すると、物体Aがばねから受ける力は
,kのうち必要なものを用いて表せ。ここで、重心Gから物体Aおよび物体Bまでの距離がともにdだけ減少すると、物体Aがばねから受ける力は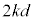 変化することを用いてもよい。
変化することを用いてもよい。 時刻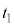 以降、物体Aはベルトに対して静止し続けた。
以降、物体Aはベルトに対して静止し続けた。
(5) 時刻t (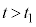 )における
)における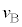 をt,V,
をt,V,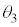 ,m,
,m,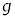 ,kのうち必要なものを用いて表せ。
,kのうち必要なものを用いて表せ。
(6) 物体Aがベルトに対して静止し続けるためにμが満たすべき条件を、V,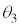 ,m,
,m,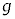 ,kのうち必要なものを用いて表せ。
,kのうち必要なものを用いて表せ。
【広告】ここから広告です。ご覧の皆さまのご支援ご理解を賜りたく、よろしくお願いいたします。
【広告】広告はここまでです。
解答 '94年以来のベルトコンベアの問題ですが、遥かに複雑で細かい神経を使う問題になっています。なぜ、斜面の傾角を設問ごとに変えているのか、と思ってしまいますが、物体をベルトに置くとき静止摩擦か動摩擦か、と考えてしまうと、問題文の状況があり得ないことになってしまうので、物体をベルトに置く時点で何らかの撃力を与えて最初から動摩擦だった、と考えればよいようです。
Ⅲでは、重心から見たり、Aから見たり、混乱し易いので注意してください。
Ⅰ 物体Aが斜面から受ける垂直抗力Nは、重力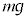 の斜面に垂直な方向成分
の斜面に垂直な方向成分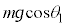 とつり合うので、
とつり合うので、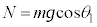 です。よって、物体Aに、斜面に沿う方向に働く動摩擦力の大きさは
です。よって、物体Aに、斜面に沿う方向に働く動摩擦力の大きさは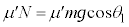 ,最大静止摩擦力の大きさは
,最大静止摩擦力の大きさは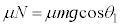 です(摩擦力を参照)。それぞれの摩擦力の向きは、運動を妨げる向きです。
です(摩擦力を参照)。それぞれの摩擦力の向きは、運動を妨げる向きです。
物体Aに初速度を与えたとき斜面に沿って上昇したので、物体Aに働く摩擦力は、斜面に沿って下向きの動摩擦力で、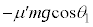 ,物体には、斜面に沿って下向きに重力
,物体には、斜面に沿って下向きに重力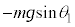 も働くので、物体Aの斜面に沿う方向の運動方程式は、加速度をaとして、
も働くので、物体Aの斜面に沿う方向の運動方程式は、加速度をaとして、 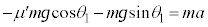 ∴
∴ 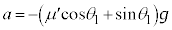
∴ 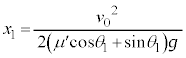 ......[答]
......[答]
(2) 最高点で物体Aは一旦停止し、摩擦力が静止摩擦力f に変わります。最高点での力のつり合いより、
最高点で滑り出すのでf は最大静止摩擦力を越えます。
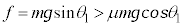 ∴
∴ 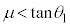
最高点から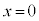 に戻るまでの変位は
に戻るまでの変位は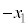 です。この間、物体Aは下向きに動きますが、この間の摩擦力は、上向きの動摩擦力
です。この間、物体Aは下向きに動きますが、この間の摩擦力は、上向きの動摩擦力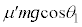 です。
です。
物体Aの斜面に沿う方向の運動方程式は、加速度をaとして、 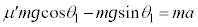 ∴
∴ 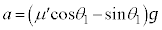
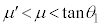 なので
なので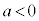 です。物体Aが
です。物体Aが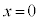 に戻ったときの速度を
に戻ったときの速度を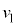 (
(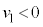 )として、等加速度運動の公式より、
)として、等加速度運動の公式より、(1)の結果を代入して、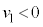 より、
より、 ∴ 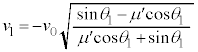 ......[答]
......[答]
Ⅱ(1) 物体Aの初速度が0で、ベルトとともに速度Vで上昇しないので、物体Aはベルトに対して最初から滑っていて、摩擦力は最初から動摩擦力だったと考えます。物体Aには下向きの重力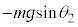 が働き、動摩擦力は上向きで
が働き、動摩擦力は上向きで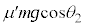 です。物体Aの運動方程式は、加速度をaとして、
です。物体Aの運動方程式は、加速度をaとして、 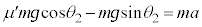 ∴
∴ 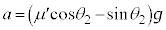
物体Aは上向きに上昇し始めるので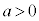 ,つまり、
,つまり、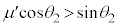 ,
,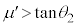 です。
です。
物体Aが等加速度運動する間、物体Aの速度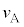 は、
は、 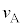 は時間とともに増大するので、やがて速度Vになり得ます。
は時間とともに増大するので、やがて速度Vになり得ます。とすると、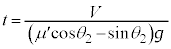 (
(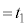 とします。)となりますが、
とします。)となりますが、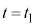 になった時点で
になった時点で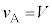 となり、物体Aはベルトに対して静止し、摩擦力が静止摩擦力に変わります。静止摩擦力f は重力とつり合うので、
となり、物体Aはベルトに対して静止し、摩擦力が静止摩擦力に変わります。静止摩擦力f は重力とつり合うので、 です。
です。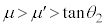 となるので、
となるので、 であり、静止摩擦力f は、最大静止摩擦力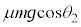 を越えません。つまり
を越えません。つまり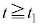 においては、物体Aは、ベルトともに速度Vで移動します。よって、
においては、物体Aは、ベルトともに速度Vで移動します。よって、 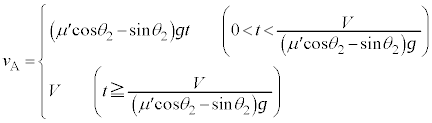 ......[答]
......[答]
(2) 物体Aに下向きの初速度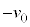 (
(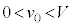 )を与えて、再び
)を与えて、再び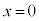 に戻ったということは、物体Aの加速度
に戻ったということは、物体Aの加速度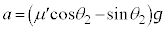 は
は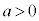 です。物体Aの運動は等加速度運動なので、鉛直投げ上げの運動と同様に、
です。物体Aの運動は等加速度運動なので、鉛直投げ上げの運動と同様に、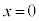 で物体Aの速度
で物体Aの速度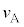 が、
が、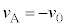 であれば、
であれば、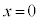 に戻った時の物体Aの速度は大きさは等しく向きが逆で、
に戻った時の物体Aの速度は大きさは等しく向きが逆で、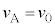 ......[答]
......[答]
Ⅲ 物体Aに働く力は、上向きの動摩擦力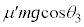 ,下向きの重力
,下向きの重力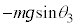 ,下向きのばねの弾性力
,下向きのばねの弾性力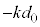 で、これらの力のつり合いより、
で、これらの力のつり合いより、 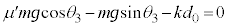 ・・・①
・・・①
(1) 物体Bに働く力は、下向きの重力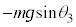 ,上向きのばねの弾性力
,上向きのばねの弾性力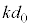 で、これらの力のつり合いより、
で、これらの力のつり合いより、 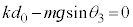 ・・・②
・・・②∴ 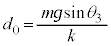 ......[答]
......[答]
(2) (1)の結果を①に代入して、
∴ 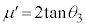 ......[答]
......[答] ベルト上で、物体A,物体Bの座標を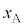 ,
,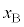 とします。ばねの自然長の長さをLとすると、ばねの伸びは
とします。ばねの自然長の長さをLとすると、ばねの伸びは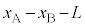 です。①の弾性力は
です。①の弾性力は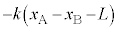 となり、②の弾性力は
となり、②の弾性力は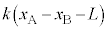 となります。物体A,物体Bの加速度を
となります。物体A,物体Bの加速度を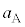 ,
,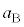 として、物体Aの運動方程式は、
として、物体Aの運動方程式は、 このうち、(2)の結果を用いて、
より、物体Aの運動方程式は、
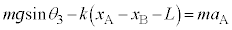 ・・・③
・・・③物体Bの運動方程式は、
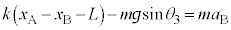 ・・・④
・・・④
(3) ③+④より、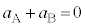
即ち、重心の加速度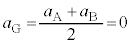 より、重心は等速度運動をします。
より、重心は等速度運動をします。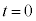 において、
において、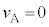 ,
,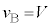 なので重心の速度は
なので重心の速度は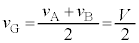 です。よって、時刻t における重心の速度は、
です。よって、時刻t における重心の速度は、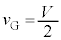 ......[答]
......[答]
(4) 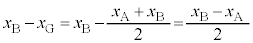 ,
,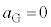 ,④より、
,④より、 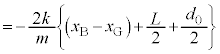 (∵ (1)の結果より
(∵ (1)の結果より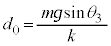 )
)これより、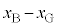 (重心から見た物体B)は、角振動数
(重心から見た物体B)は、角振動数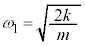 ,振動中心
,振動中心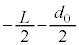 の単振動をします。
の単振動をします。
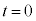 以前に物体Bは、物体Aの位置(
以前に物体Bは、物体Aの位置(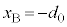 )から
)から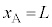 だけ下がった位置で静止していました。
だけ下がった位置で静止していました。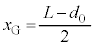 において、
において、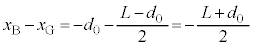 ,
,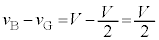 なので、このとき、
なので、このとき、 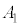 ,
,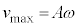 ・・・⑤
・・・⑤つまり物体Bは振動中心にいます。このとき重心から見た物体Bの相対速度は(3)の結果より、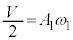 ,よって、単振動の振幅を
,よって、単振動の振幅を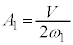 として、角振動数は
として、角振動数は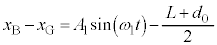 なので、単振動の公式:
なので、単振動の公式: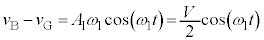 より、
より、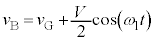 ,これより、
,これより、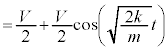 です。ばねは最初に伸びた状態だったので、物体Bは重心方向に移動し始め、⑤を考慮して、
です。ばねは最初に伸びた状態だったので、物体Bは重心方向に移動し始め、⑤を考慮して、 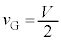 ・・・⑥
・・・⑥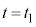 (∵
(∵ 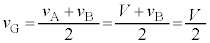 )
)∴ 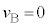
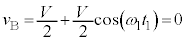 ......[答] (∵
......[答] (∵ 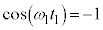 ,また、(3)の結果より
,また、(3)の結果より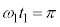 )
)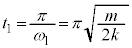 に物体Aがベルトと同じ速度Vになると、
に物体Aがベルトと同じ速度Vになると、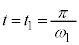 より、
より、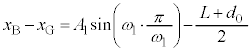 です。
です。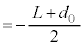 ・・・⑦
・・・⑦として、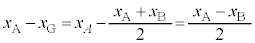 より、はじめてこうなるのは、
より、はじめてこうなるのは、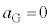 のときで、
のときで、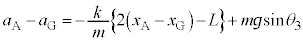 より、
より、 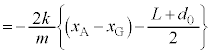 ......[答] (これは単振動の半周期です)
......[答] (これは単振動の半周期です)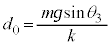 において、⑥より、
において、⑥より、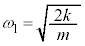 ・・・⑧
・・・⑧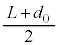 ,
,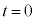 ,③より、
,③より、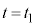 (∵ (1)の結果より
(∵ (1)の結果より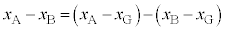 )
)これより、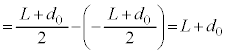 (重心から見た物体A)は、角振動数
(重心から見た物体A)は、角振動数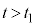 ,振動中心
,振動中心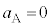 の単振動をします。
の単振動をします。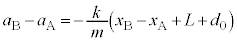 において、⑤より、
において、⑤より、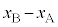 となるので、物体Aは振動中心にいます。半周期後
となるので、物体Aは振動中心にいます。半周期後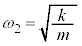 に、重心から見て物体Aは振動中心
に、重心から見て物体Aは振動中心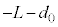 に戻り、
に戻り、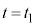 のときの⑧より、
のときの⑧より、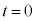 において、
において、 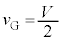 ・・・⑨
・・・⑨
注.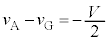 において、
において、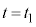 ,
,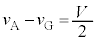 なので
なので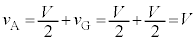 です。半周期後
です。半周期後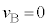 には、速度の向きが変わり
には、速度の向きが変わり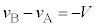 ,従って、
,従って、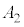 となり、
となり、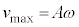 では摩擦力が静止摩擦力に変わり、物体Aは静止し続けます。
では摩擦力が静止摩擦力に変わり、物体Aは静止し続けます。 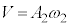 において、物体Aはベルトに対し静止するので、ベルトとともに速度Vで等速度運動し、
において、物体Aはベルトに対し静止するので、ベルトとともに速度Vで等速度運動し、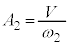 です。これと(1)の結果、また④より、
です。これと(1)の結果、また④より、これより、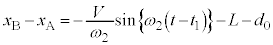 (物体Aから見た物体B)は、角振動数
(物体Aから見た物体B)は、角振動数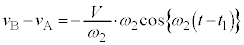 ,振動中心
,振動中心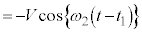 の単振動をします。⑨より、
の単振動をします。⑨より、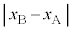 に物体Bは振動中心にいます。
に物体Bは振動中心にいます。
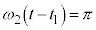 において
において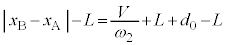 ,また、⑦より
,また、⑦より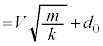 なので、
なので、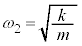 です。
です。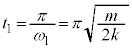 の単振動の振幅を
の単振動の振幅を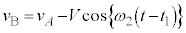 として、角振動数は
として、角振動数は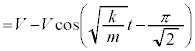 なので、単振動の公式:
なので、単振動の公式: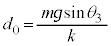 より、
より、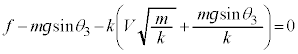 となり、
となり、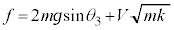
よって、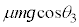 において、振動中心(
において、振動中心(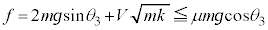 )から、ばねは伸びようとする状態にあるので、物体Bは、物体Aに対して下向きに運動を始め、
)から、ばねは伸びようとする状態にあるので、物体Bは、物体Aに対して下向きに運動を始め、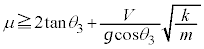 において、
において、 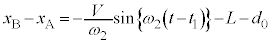 ・・・⑩
・・・⑩微分すると、
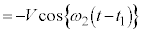 ・・・⑪
・・・⑪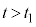 において、⑩より、
において、⑩より、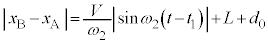 は
は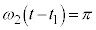 のときに最大になり最大値は
のときに最大になり最大値は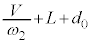 です。ばねの伸びの最大値は、
です。ばねの伸びの最大値は、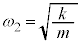 より、
より、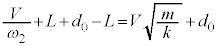 ・・・⑫
・・・⑫
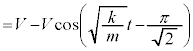 ......[答]
......[答]
(6) ばねの伸びが最大になるとき、物体Aに働く静止摩擦力をf として、物体Aに働く力は、上向きの静止摩擦力f,下向きの重力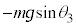 ,下向きのばねの弾性力
,下向きのばねの弾性力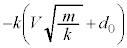 (ばねの伸びの最大値は⑫)です。物体Aに働く力のつり合いより、⑫と(1)の結果
(ばねの伸びの最大値は⑫)です。物体Aに働く力のつり合いより、⑫と(1)の結果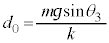 を用いて、
を用いて、 物体Aがベルトに対して静止し続けるためには、f が最大静止摩擦力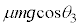 を越えないことが条件で、
を越えないことが条件で、 ∴ 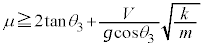 ......[答]
......[答]
【広告】ここから広告です。ご覧の皆さまのご支援ご理解を賜りたく、よろしくお願いいたします。
【広告】広告はここまでです。
東大物理TOP 物理TOP TOPページに戻る
【広告】ここから広告です。ご覧の皆さまのご支援ご理解を賜りたく、よろしくお願いいたします。
【広告】広告はここまでです。
各問題の著作権は
出題大学に属します。©2005-2024(有)りるらる 苦学楽学塾 随時入会受付中!理系大学受験ネット塾苦学楽学塾(ご案内はこちら)ご入会は、
まず、こちらまでメールを
お送りください。 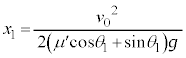 ......[答]
......[答]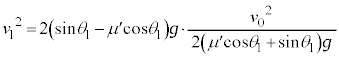
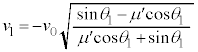 ......[答]
......[答]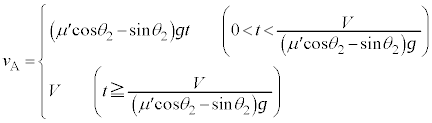 ......[答]
......[答]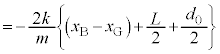 (∵ (1)の結果より
(∵ (1)の結果より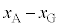
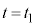 (∵ (1)の結果より
(∵ (1)の結果より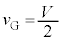 ・・・⑨
・・・⑨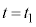
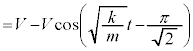 ......[答]
......[答]