早大教育物理'05年[2]
(A) オシロスコープの原理
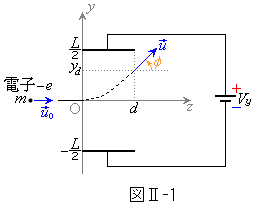
図Ⅱ-1のように、速度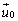
の電子(電荷は
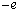，質量はm)がz軸上を入射してくる。以下では重力や地磁気は無視できるものとする。
間隔Lの極板には電圧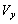
がかかっている。極板は
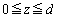にわたっているので電子はこの間で力を受け、その結果生じる加速度のy成分は (1) である。電子のz座標がdであるとき、速度のy成分は (2) であり、z成分は
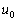のままである。また、このときのy座標は[ (3)
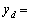]である。さらにこのとき電子の進行方向がz軸と角度ϕをなしているとすると、
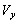を用いて[ (4) 
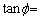]と書ける。電圧
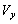を上げすぎると電子は極板に衝突してしまう。衝突しない条件は[ (5) 
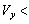]である。ただし、
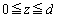における極板間では電場(電界)は一様であり、その外ではゼロとみなしてよい。
(B) 位相差の測定
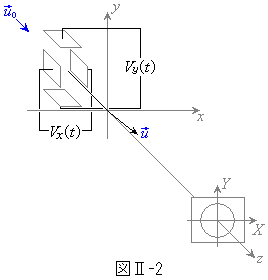
2組の極板を用いて図Ⅱ-2のように電子ビームの角度をx方向にも制御できるようにした。電子は極板の領域を抜けた後その速度を保って進み、極板の大きさに比べて極めて遠方の蛍光板(ブラウン管)に当たってその点(スポット)を光らせる。極板の大きさLおよびdは蛍光板までの距離に比べて無視できるほど小さいので、以下では電子は原点Oから飛び出すという近似を用いる。極板にかける電圧を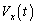
，
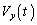のように時間的に変化させると、蛍光板のスポットの座標も
，
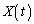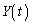のように時間の関数となる。(A)より
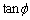は電圧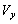
に比例するので、電子が極板から蛍光板に到達する時間を無視すれ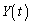ば
は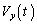
に比例し、また
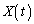も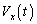
に比例するとしてよい。
問1 原点Oから蛍光板までの距離をDとする。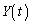
を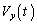
を用いて表せ。 問2 極板に角振動数(角周波数)ω の電圧をかけたとき、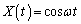
，
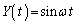となったとする。
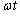を消去し、蛍光面に表示されるXとYで表現される図形の方程式を求めよ。 問3 同様に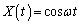
，
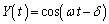となった場合に、表示される図形の方程式を求め、以下の空欄をδ の関数で埋めよ。δ は位相差と呼ばれる。 
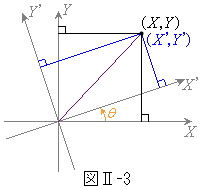問4 図Ⅱ-3のような座標回転
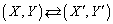によって問3で得た方程式を
，
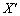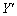で表し、積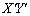
の係数が0となるようにθ を求めよ。そのようなθ のうち、
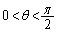となるθ は[ 
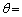]である。このとき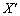
，
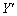で表した図形の方程式は である。これは楕円の方程式であり、
が位相差δ の関数となるので、この比を測定することにより位相差を求めることができる。
問5 位相差δ を求めるもう一つの方法がある。問3の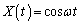
，
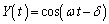から直接 を計算すると右辺はδ のみの関数となる。上記の空欄を埋めよ。ただし<...>は、1周期についての時間平均を表す。
【広告】ここから広告です。ご覧の皆さまのご支援ご理解を賜りたく、よろしくお願いいたします。
【広告】広告はここまでです。
解答 問2以降は、物理の入試問題なのか？と思ってしまいます。
(1) 極板間にはy軸負方向に大きさ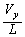
の電場(電界)ができています。負電荷をもつ電子にはy軸正方向に大きさ
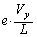の力が働いています。加速度のy成分を
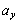としてy軸方向の運動方程式： ∴ 
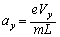......[答] (
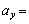一定 なので、y軸方向の運動は等加速度運動です) (2) z軸方向に速さ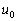
で距離dの極板間を通過するのに時間
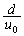を要します。
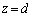のとき、電子の速度のy成分
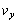は、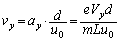 
......[答]
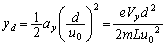......[答](4) 電子の速度はz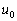成分が
，y成分が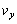
なので、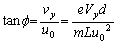 
......[答](5) 電子が極板に衝突しない条件は、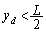
∴ 
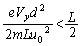
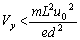......[答]
問1 極板間を通り抜けた後、電子はzx平面となす角ϕの方向に等速直線運動します。電子が原点Oから飛び出す近似を用いると、y方向の変位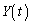
は、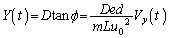 
......[答]追記．2組の極板とも、z軸方向の幅がdで、極板間距離がLだとします。電子の進行方向がyz平面となす角度をφとすれば(4)と同様に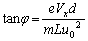
となります。問1と同様にして、x方向の変位
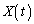についても、
問2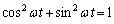 
より、 図形の方程式は、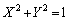
(∵ 
)∴ 
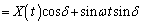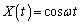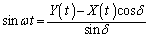
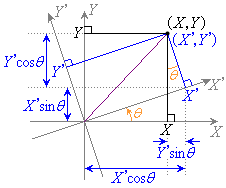問4 右図より、問3の結果に代入して
積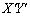
の係数を0とすると、 題意より位相差δ は、いろいろな値をとり得るので、
このとき①より、
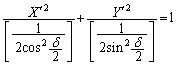......[答]
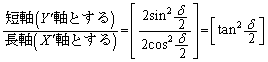......[答] (楕円を参照)注．上記では、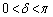
とします。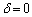
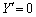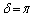のときは
，
のときは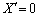
となり楕円にはなりません。
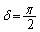のときは円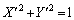
になります。
問5 周期Tで変化する量があって、時刻tにおける値を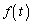
とするとき、周期Tをn等分して時刻
，
，･･･，
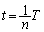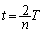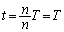におけるn個の値の平均値
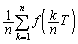を考え、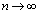
の極限値を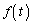
の1周期にわたる時間平均
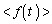と考えることができます。つまり、 として計算できます。
，
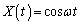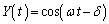のとき、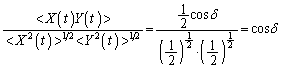 
......[答]
【広告】ここから広告です。ご覧の皆さまのご支援ご理解を賜りたく、よろしくお願いいたします。
【広告】広告はここまでです。
物理TOP TOPページに戻る
【広告】ここから広告です。ご覧の皆さまのご支援ご理解を賜りたく、よろしくお願いいたします。
【広告】広告はここまでです。
各問題の著作権は
出題大学に属します。©2005-2024(有)りるらる 苦学楽学塾 随時入会受付中！理系大学受験ネット塾苦学楽学塾(ご案内はこちら)ご入会は、
まず、こちらまでメールを
お送りください。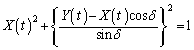 
，
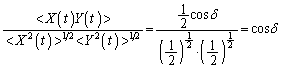ともに
を比例係数として
，
に比例します。
より、
......[答]
･･･①
より、
......[答]
，
，
より、
