複素数平面
【広告】ここから広告です。ご覧の皆さまのご支援ご理解を賜りたく、よろしくお願いいたします。
【広告】広告はここまでです。
複素数の図形的応用について学習します。複素数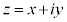
(x，yは実数、iは虚数単位、つまり
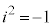)の実部xをx座標、虚部yをy座標として、複素数zに対して座標平面上の点
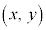を対応させたものを考えます。この平面が複素数平面です。
ここで学習する内容は、以下の通りです。各項目をクリックしてください。
複素数平面 図形的応用を考える上での複素数平面の基礎事項を学びます。
絶対値 複素数平面上で複素数の表す点と原点との距離が絶対値です。
偏角 複素数zの表す点と原点(極と言います)を結ぶ線分とx軸とのなす角を偏角と言います。
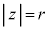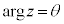極形式 複素数zについて、
，
として、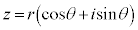
と表すとき、これを極形式と言います。
ド・モアブルの定理 整数nについて、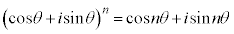
が成立します。
1の累乗根 1のn乗根となる複素数は、複素数平面上で正n角形の頂点に並びます。
複素数平面上の回転 図形的応用を考える上での基礎技巧となる回転について学習します。
複素数平面の図形的応用 直角二等辺三角形、正三角形、図形の変換などの応用を学習します。
【広告】ここから広告です。ご覧の皆さまのご支援ご理解を賜りたく、よろしくお願いいたします。
【広告】広告はここまでです。
数学基礎事項TOP 数学TOP TOPページに戻る
【広告】ここから広告です。ご覧の皆さまのご支援ご理解を賜りたく、よろしくお願いいたします。
【広告】広告はここまでです。
各問題の著作権は
出題大学に属します。©2005-2024(有)りるらる 苦学楽学塾 随時入会受付中！理系大学受験ネット塾苦学楽学塾(ご案内はこちら)ご入会は、
まず、こちらまでメールを
お送りください。