�@���ʃe�X�g���wIIB '24�N��2��@
m��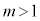 �����萔�Ƃ��A
�����萔�Ƃ��A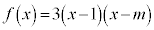 �Ƃ���B�܂��A
�Ƃ���B�܂��A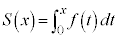 �Ƃ���B��
�Ƃ���B��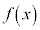 ��
��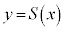 �̃O���t�̊W�ɂ��čl���Ă݂悤�B
�̃O���t�̊W�ɂ��čl���Ă݂悤�B
(1) 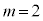 �̂Ƃ��A���Ȃ킿�A
�̂Ƃ��A���Ȃ킿�A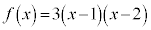 �̂Ƃ����l����B
�̂Ƃ����l����B (i) 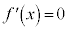 �ƂȂ�x�̒l��
�ƂȂ�x�̒l��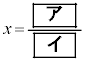 �ł���B(ii)
�ł���B(ii) 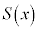 ���v�Z����ƁA
���v�Z����ƁA �ł��邩��
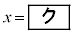 �̂Ƃ��A
�̂Ƃ��A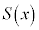 �͋ɑ�l
�͋ɑ�l ���Ƃ�
���Ƃ�
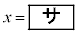 �̂Ƃ��A
�̂Ƃ��A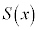 �͋ɏ��l
�͋ɏ��l ���Ƃ邱�Ƃ��킩��B
���Ƃ邱�Ƃ��킩��B (iii) 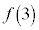 �ƈ�v������̂Ƃ��āA����
�ƈ�v������̂Ƃ��āA���� �`
�` �̂����A���������̂�
�̂����A���������̂� �ł���B
�ł���B  �̉Q
�̉Q �@
�@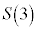
 �@��
�@��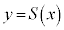 �̃O���t��̓_
�̃O���t��̓_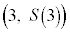 �ɂ�����ڐ��̌X��
�ɂ�����ڐ��̌X�� �@��
�@��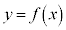 �̃O���t��̓_
�̃O���t��̓_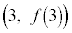 �ɂ�����ڐ��̌X��
�ɂ�����ڐ��̌X��
(2) 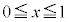 �͈̔͂ŁA��
�͈̔͂ŁA��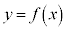 �̃O���t��x�������y���ň͂܂ꂽ�}�`�̖ʐς�
�̃O���t��x�������y���ň͂܂ꂽ�}�`�̖ʐς�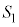 �C
�C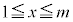 �͈̔͂ŁA��
�͈̔͂ŁA��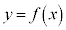 �̃O���t��x���ň͂܂ꂽ�}�`�̖ʐς�
�̃O���t��x���ň͂܂ꂽ�}�`�̖ʐς�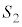 �Ƃ���B���̂Ƃ��A
�Ƃ���B���̂Ƃ��A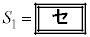 �C
�C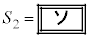 �ł���B
�ł���B 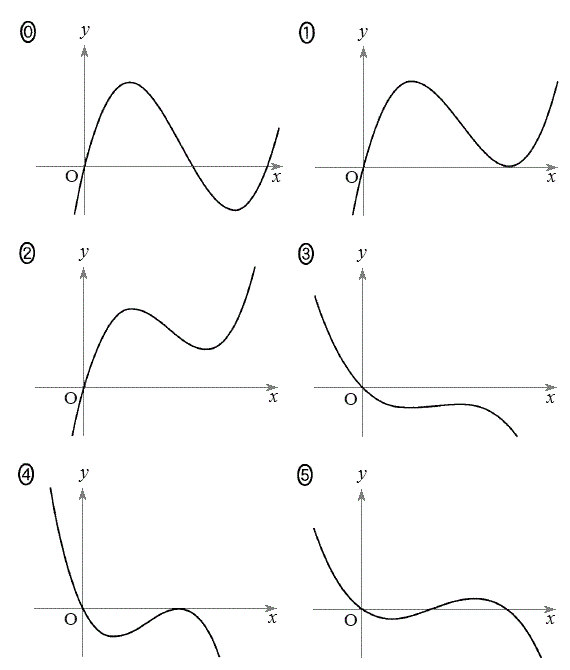
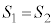 �ƂȂ�̂�
�ƂȂ�̂�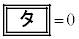 �̂Ƃ��ł��邩��A
�̂Ƃ��ł��邩��A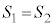 �����藧�悤��
�����藧�悤��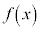 �ɑ����
�ɑ����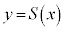 �̃O���t�̊T�`��
�̃O���t�̊T�`�� �ł���B�܂��A
�ł���B�܂��A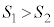 �����藧�悤��
�����藧�悤��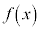 �ɑ����
�ɑ����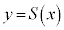 �̃O���t�̊T�`��
�̃O���t�̊T�`�� �ł���B
�ł���B
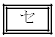 �C
�C �̉Q(�������̂��J��Ԃ��I��ł��悢�B)
�̉Q(�������̂��J��Ԃ��I��ł��悢�B) �@
�@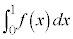 �@�@
�@�@ �@
�@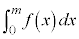 �@�@
�@�@ �@
�@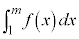
 �@
�@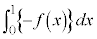 �@�@
�@�@ �@
�@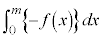 �@�@
�@�@ �@
�@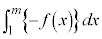
 �̉Q
�̉Q �@
�@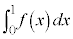 �@�@
�@�@ �@
�@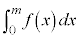
 �@
�@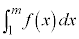 �@�@
�@�@ �@
�@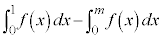
 �@
�@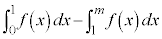 �@�@
�@�@ �@
�@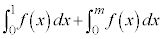
 �@
�@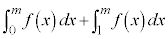
 �C
�C �ɂ��ẮA�ł��K���Ȃ��̂��A�E�}��
�ɂ��ẮA�ł��K���Ȃ��̂��A�E�}�� �`
�` �̂����������I�ׁB�������A�������̂��J��Ԃ��I��ł��悢�B
�̂����������I�ׁB�������A�������̂��J��Ԃ��I��ł��悢�B
(3) ��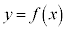 �̃O���t�̓��������
�̃O���t�̓��������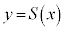 �̃O���t�̓������l���Ă݂悤�B
�̃O���t�̓������l���Ă݂悤�B ��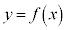 �̃O���t�͒���
�̃O���t�͒��� �Ɋւ��đΏ̂ł��邩��A���ׂĂ̐��̎���p�ɑ���
�Ɋւ��đΏ̂ł��邩��A���ׂĂ̐��̎���p�ɑ��� 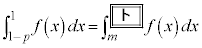 �@����@
�@����@�����藧���A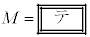 �Ƃ�����
�Ƃ�����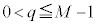 �ł��邷�ׂĂ̎���q�ɑ���
�ł��邷�ׂĂ̎���q�ɑ��� 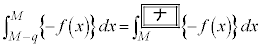 �@����A
�@����A�����藧���Ƃ��킩��B���ׂĂ̎���α�Cβ�ɑ���
�����藧���Ƃɒ��ӂ���A�@�ƇA�͂��ꂼ��
�ƂȂ�B
�ȏォ��A���ׂĂ̐��̎���p�ɑ��āA2�_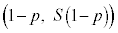 �C
�C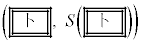 �����Ԑ����̒��_�ɂ��Ă̋L�q�Ƃ��āA���
�����Ԑ����̒��_�ɂ��Ă̋L�q�Ƃ��āA��� �`
�` �̂����A�ł��K���Ȃ��̂�
�̂����A�ł��K���Ȃ��̂� �ł���B
�ł���B
 �̉Q
�̉Q  �̉Q
�̉Q �̉Q
�̉Q �@
�@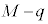 �@�@
�@�@ �@M�@�@
�@M�@�@ �@
�@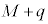
 �@
�@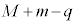 �@�@
�@�@ �@
�@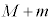 �@�@
�@�@ �@
�@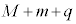
 �̉Q
�̉Q �@
�@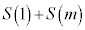 �@�@
�@�@ �@
�@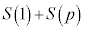 �@�@
�@�@ �@
�@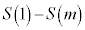
 �@
�@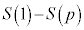 �@�@
�@�@ �@
�@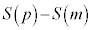 �@�@
�@�@ �@
�@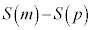
 �̉Q
�̉Q �̉Q
�̉Q �@x���W��p�̒l�ɂ�炸��ɒ�܂�Ay���W��p�̒l�ɂ��ς��B
�@x���W��p�̒l�ɂ�炸��ɒ�܂�Ay���W��p�̒l�ɂ��ς��B �@x���W��p�̒l�ɂ��ς��Ay���W��p�̒l�ɂ�炸��ɒ�܂�B
�@x���W��p�̒l�ɂ��ς��Ay���W��p�̒l�ɂ�炸��ɒ�܂�B �@���_��p�̒l�ɂ�炸��ɒ�܂�A��
�@���_��p�̒l�ɂ�炸��ɒ�܂�A��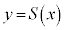 �̃O���t��ɂ���B
�̃O���t��ɂ���B �@���_��p�̒l�ɂ�炸��ɒ�܂�A��
�@���_��p�̒l�ɂ�炸��ɒ�܂�A��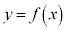 �̃O���t��ɂ���B
�̃O���t��ɂ���B �@���_��p�̒l�ɂ���ē������A�˂Ɋ�
�@���_��p�̒l�ɂ���ē������A�˂Ɋ�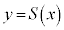 �̃O���t��ɂ���B
�̃O���t��ɂ���B �@���_��p�̒l�ɂ���ē������A�˂Ɋ�
�@���_��p�̒l�ɂ���ē������A�˂Ɋ�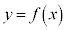 �̃O���t��ɂ���B
�̃O���t��ɂ���B
�y�L���z��������L���ł��B�����̊F���܂̂��x�������������肽���A��낵�����肢�������܂��B
�y�L���z�L���͂����܂łł��B
���@���ł͂Ȃ��̂ł����A�����������ۊ��̖���ь��������������̂ŁA���Ă����ۂ��œ������l�����������̂ł́H�ł����A�_���I�ɒǂ�Ȃ��Ă��A�O���t��`���čl����A�\�ł��B
(1) 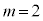 �̂Ƃ��A�B�́A
�̂Ƃ��A�B�́A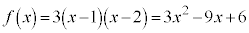
(i) ��������ƁA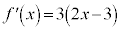 �C
�C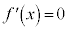 �Ƃ���ƁA
�Ƃ���ƁA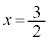 �@�A 3�@�C 2 ......[��]
�@�A 3�@�C 2 ......[��] (ii) �C��(�s��ϕ����Q��)�A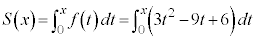 �@�E 9�@�G 6 ......[��]
�@�E 9�@�G 6 ......[��] 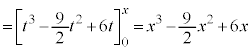 �@(��ϕ����Q��)�@�I 9�@�J 2�@�L 6 ......[��]
�@(��ϕ����Q��)�@�I 9�@�J 2�@�L 6 ......[��]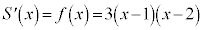 �@(��ϕ��Ɣ������Q��)
�@(��ϕ��Ɣ������Q��)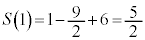 �C
�C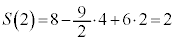 �����\�͈ȉ��B
�����\�͈ȉ��B
�����\���A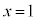 �̂Ƃ��A
�̂Ƃ��A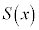 �͋ɑ�l
�͋ɑ�l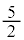 ���Ƃ�A
���Ƃ�A
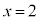 �̂Ƃ��A
�̂Ƃ��A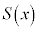 �͋ɏ��l2���Ƃ�܂��B�@�N 1�@�P 5�@�R 2�@�T 2�@�V 2 ......[��]
�͋ɏ��l2���Ƃ�܂��B�@�N 1�@�P 5�@�R 2�@�T 2�@�V 2 ......[��](iii) 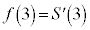 �́A
�́A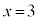 �ɂ�����
�ɂ�����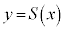 ���ڐ��̌X���ł��B�@�X 3 ......[��]
���ڐ��̌X���ł��B�@�X 3 ......[��]
(2) �B�C�C���A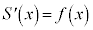 �C
�C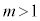 ���A
���A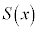 ��
��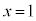 �ŋɑ�l
�ŋɑ�l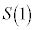 ���Ƃ�A
���Ƃ�A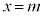 �ŋɏ��l
�ŋɏ��l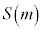 ���Ƃ�܂��B
���Ƃ�܂��B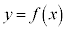 �̃O���t��x�������y���ň͂܂ꂽ�}�`���ʐ�
�̃O���t��x�������y���ň͂܂ꂽ�}�`���ʐ�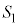 �́A
�́A 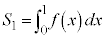 �@�Z 0 ......[��]
�@�Z 0 ......[��]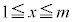 �͈̔͂ŁA
�͈̔͂ŁA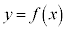 �̃O���t��x���ň͂܂ꂽ�}�`�̖ʐ�
�̃O���t��x���ň͂܂ꂽ�}�`�̖ʐ�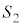 �́A���͈̔͂�
�́A���͈̔͂�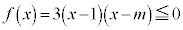 �Ȃ̂ŁA
�Ȃ̂ŁA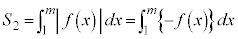 �@�\ 5 ......[��]
�@�\ 5 ......[��]�C���A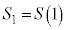 �ł��B�܂��A
�ł��B�܂��A �����A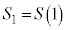 �C
�C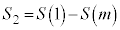 �@����D
�@����D
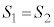 �ƂȂ�̂́A�D���A
�ƂȂ�̂́A�D���A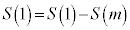 �C����āA
�C����āA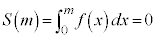 �@�^ 1 ......[��]�ɏ��l
�@�^ 1 ......[��]�ɏ��l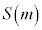 ��0�ɂȂ��Ă���
��0�ɂȂ��Ă���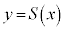 �̃O���t��
�̃O���t�� �ł��B�@�` 1 ......[��]
�ł��B�@�` 1 ......[��]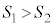 �ƂȂ�̂́A�D���A
�ƂȂ�̂́A�D���A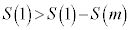 �C����āA
�C����āA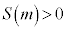 �C�ɏ��l
�C�ɏ��l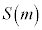 �����ł���
�����ł���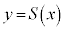 �̃O���t��
�̃O���t�� �ł��B�@�c 2 ......[��]
�ł��B�@�c 2 ......[��]
(3) 2����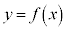 �̃O���t�͕������Ŏ��Ɋւ��đΏ̂ł��B�@���
�̃O���t�͕������Ŏ��Ɋւ��đΏ̂ł��B�@���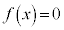 �̉���
�̉���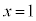 �C
�C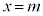 �ł��邱�Ƃ���A���̈ʒu��
�ł��邱�Ƃ���A���̈ʒu��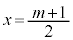 �ł��B�@�e 3 ......[��]
�ł��B�@�e 3 ......[��] 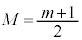 �Ƃ����ƁA
�Ƃ����ƁA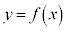 �̃O���t�́A���F
�̃O���t�́A���F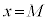 �Ɋւ��đΏ̂Ȃ̂ŁA���ׂĂ̐��̎���p�ɑ��āA
�Ɋւ��đΏ̂Ȃ̂ŁA���ׂĂ̐��̎���p�ɑ��āA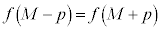 �ł����āA
�ł����āA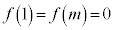 ��
��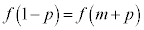 �ł��邱�Ƃ���A
�ł��邱�Ƃ���A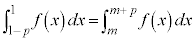 �@����@�@�g 4 ......[��]
�@����@�@�g 4 ......[��]�܂��A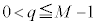 �ł��邷�ׂĂ̎���q�ɑ��āA
�ł��邷�ׂĂ̎���q�ɑ��āA 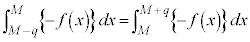 �@����A�@�i 2 ......[��]
�@����A�@�i 2 ......[��]�@���A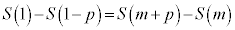
�� 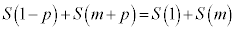 �@����E�@ �j 0 ......[��]�A���A
�@����E�@ �j 0 ......[��]�A���A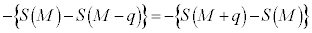
���@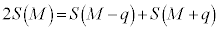 �@����F�@�k 4 ......[��]
�@����F�@�k 4 ......[��]
2�_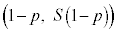 �C
�C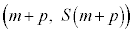 �̒��_�́Ax���W��
�̒��_�́Ax���W��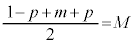 �Cy���W�́A�E���A
�Cy���W�́A�E���A �A�ɂ�����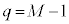 �ƌ���A�F���A
�ƌ���A�F���A �ł����āA���_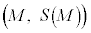 ��
��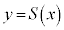 ��̓_�ł��邱�Ƃ�������܂��B�@�l 2 ......[��]
��̓_�ł��邱�Ƃ�������܂��B�@�l 2 ......[��] ���D���w�V�͈̔͂ɂȂ�܂����A���̒��_�́A3�����̃O���t�̕ϋȓ_�ł��B3�����̃O���t�͕ϋȓ_�Ɋւ��đΏ̂ł��B
�y�L���z��������L���ł��B�����̊F���܂̂��x�������������肽���A��낵�����肢�������܂��B
�y�L���z�L���͂����܂łł��B
�@�@���wTOP�@�@TOP�y�[�W�ɖ߂�
�y�L���z��������L���ł��B�����̊F���܂̂��x�������������肽���A��낵�����肢�������܂��B
�y�L���z�L���͂����܂łł��B
�e���̒��쌠��
�o���w�ɑ����܂��B©2005-2024(�L)����� ��w�y�w�m ���������t���I���n��w�l�b�g�m��w�y�w�m(���ē���������)������́A
�܂��A������܂Ń��[����
�����肭�������B  �ł���B
�ł���B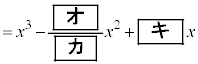
 ���Ƃ�
���Ƃ�