�k�嗝�n���w'07�N�O��[5]
�ȉ~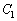 �F
�F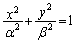 �Ƒo�Ȑ�
�Ƒo�Ȑ� �F
�F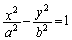 ���l����B
���l����B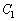 ��
��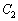 �̏œ_����v���Ă���Ȃ�A
�̏œ_����v���Ă���Ȃ�A ��
��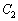 �̌�_�ł��ꂼ��̐ڐ��͒������邱�Ƃ������B
�̌�_�ł��ꂼ��̐ڐ��͒������邱�Ƃ������B
�y�L���z��������L���ł��B�����̊F���܂̂��x�������������肽���A��낵�����肢�������܂��B
�y�L���z�L���͂����܂łł��B
���@2���Ȑ��Ɋւ���ؖ��������Ă����܂��B2���Ȑ��Ɋւ������̍��ڂɂ����낢��ȗ�������Ă��܂��̂ŎQ�Ƃ��Ă��������B
�ȉ~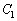 �̏œ_�́A
�̏œ_�́A �̂Ƃ���x�����
�̂Ƃ���x����� �C
�C �̂Ƃ���y�����
�̂Ƃ���y�����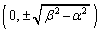 �ɂ���܂��B
�ɂ���܂��B
�o�Ȑ�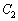 �̏œ_��x�����
�̏œ_��x����� �ɂ���܂��B
�ɂ���܂��B
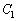 ��
�� �̏œ_����v����Ƃ������Ƃ́A�œ_��x����ɂ����āA
�̏œ_����v����Ƃ������Ƃ́A�œ_��x����ɂ����āA �ł���A
�ł���A
 �@����@
�@����@
�܂��A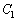 �C
�C �̌�_��
�̌�_��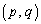 �Ƃ���ƁA��_�́A
�Ƃ���ƁA��_�́A ��̓_�ł�
��̓_�ł� ��̓_�ł�����̂ŁA
��̓_�ł�����̂ŁA
 �@����A
�@����A
 �@����B
�@����B
�����ŁA ���Ƃ���ƁA�A�C�B���A
���Ƃ���ƁA�A�C�B���A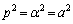 �ƂȂ�܂����A���̂Ƃ��A�@���A
�ƂȂ�܂����A���̂Ƃ��A�@���A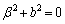 �C�����A
�C�����A �ƂȂ��Ă��܂��̂ŁA
�ƂȂ��Ă��܂��̂ŁA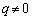
�_ �ɂ�����ȉ~
�ɂ�����ȉ~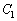 �̐ڐ��́A
�̐ڐ��́A
�ł����āA���̌X���́A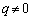 �̂Ƃ��A
�̂Ƃ��A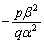 �ł��B
�ł��B
�_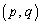 �ɂ�����o�Ȑ�
�ɂ�����o�Ȑ�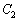 �̐ڐ��́A
�̐ڐ��́A
�ł����āA���̌X���́A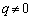 �̂Ƃ��A
�̂Ƃ��A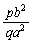 �ł��B
�ł��B
��ӂ��������߂ɂ́A���ڐ��̌X���̐ρF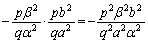 ��
�� �ɂȂ��Ă����悢(2�����̕��s�E�������Q��)�킯�ł��B
�ɂȂ��Ă����悢(2�����̕��s�E�������Q��)�킯�ł��B
�A�C�B���A
�@���A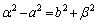
�� 
�� 
����āA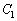 ��
��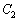 �̌�_�ł��ꂼ��̐ڐ��͒������܂��B
�̌�_�ł��ꂼ��̐ڐ��͒������܂��B
�NjL�D��L�ł́A�ȉ~�̐ڐ��̌�����p���܂������A������'07�N[3]�ɂ��̌�������肪�o�肳��Ă��܂��B
�Ȑ�C�F (
( �C
�C )��̓_P
)��̓_P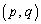 �ɂ����邱�̋Ȑ��̐ڐ���l�Ƃ���B���̂Ƃ��A���̖₢�ɓ�����B
�ɂ����邱�̋Ȑ��̐ڐ���l�Ƃ���B���̂Ƃ��A���̖₢�ɓ�����B (1) ����l�̕�������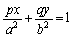 �ƂȂ邱�Ƃ������B
�ƂȂ邱�Ƃ������B (2) �_P���Ȑ�C�̑�1�ی��̕������Ƃ���B����l��x���Cy���̌�_�����ꂼ��Q�CR�Ƃ���Ƃ��A����QR�̒����̍ŏ��l�����߂�B
��(1) �_P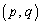 ���Ȑ�C��̓_�ł��邱�Ƃ���A
���Ȑ�C��̓_�ł��邱�Ƃ���A 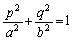 �@����@
�@����@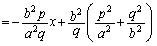
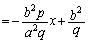 �@(�� �@)
�@(�� �@)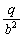 �������āA
�������āA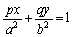 �@����A
�@����A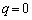 �̂Ƃ��A�_P
�̂Ƃ��A�_P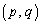 �ɂ�����Ȑ�C�̐ڐ��́A
�ɂ�����Ȑ�C�̐ڐ��́A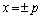
�@���A������A�Ɋ܂܂�܂��B
����āA����l�̕������́A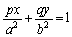
(2) �Ȑ�C��̓_P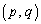 �́A
�́A 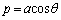 �C
�C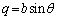
���}��ϐ��\������܂��B�_P����1�ی��̓_�̂Ƃ��ɂ� �ł��B�ڐ�l�̕������́A
�ł��B�ڐ�l�̕������́A�ƂȂ�܂��B
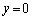 �Ƃ���x���Ƃ̌�_Q��x���W�́A
�Ƃ���x���Ƃ̌�_Q��x���W�́A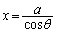
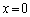 �Ƃ���y���Ƃ̌�_R��y���W�́A
�Ƃ���y���Ƃ̌�_R��y���W�́A
����QR�̒�����2��́A �s�����̓����́A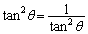 �C
�C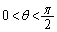 �ɂ����ẮA
�ɂ����ẮA �̂Ƃ��ɐ��藧���܂��B
�̂Ƃ��ɐ��藧���܂��B
����āA����QR�̒����̍ŏ��l�́A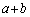 ......[��]
......[��]
�y�L���z��������L���ł��B�����̊F���܂̂��x�������������肽���A��낵�����肢�������܂��B
�y�L���z�L���͂����܂łł��B
�@�@���wTOP�@�@TOP�y�[�W�ɖ߂�
�y�L���z��������L���ł��B�����̊F���܂̂��x�������������肽���A��낵�����肢�������܂��B
�y�L���z�L���͂����܂łł��B
�e���̒��쌠��
�o���w�ɑ����܂��B©2005-2024(�L)����� ��w�y�w�m ���������t���I���n��w�l�b�g�m��w�y�w�m(���ē���������)������́A
�܂��A������܂Ń��[����
�����肭�������B