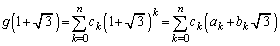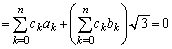��嗝�n���w'09�N���[2]
�ȉ��̖₢�ɓ�����B
(1) 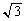 ���������ł��邱�Ƃ��ؖ�����B
���������ł��邱�Ƃ��ؖ�����B (2) a�Cb��L�����Ƃ���B������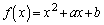 ��
��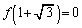 �����Ƃ��Aa�Cb�����߂�B
�����Ƃ��Aa�Cb�����߂�B (3) n��2�ȏ�̎��R���Ƃ���B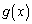 �͗L�������W���Ƃ���n���������ōō����̌W����1�ł���Ƃ���B
�͗L�������W���Ƃ���n���������ōō����̌W����1�ł���Ƃ���B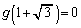 �ƂȂ�Ƃ��A
�ƂȂ�Ƃ��A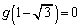 �������B
�������B
�y�L���z��������L���ł��B�����̊F���܂̂��x�������������肽���A��낵�����肢�������܂��B
�y�L���z�L���͂����܂łł��B
���@�����W����n���������F
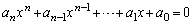
���Ap�Cq�������Ƃ��āA������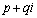 (
(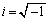 )�����ĂA���̋��f��
)�����ĂA���̋��f�� �����ɂȂ邱�Ƃ��m���Ă��܂��B
�����ɂȂ邱�Ƃ��m���Ă��܂��B
���l�ɁA�L�������W���Ƃ���n���������F

���Ap�Cq��L�����A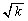 �����Ƃ��āA
�����Ƃ��āA �����Ɏ��ĂA
�����Ɏ��ĂA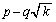 �����ɂȂ邱�Ƃ��������A�Ƃ������ł��B�Ȃ��A�������������Q�Ƃ��Ă��������B
�����ɂȂ邱�Ƃ��������A�Ƃ������ł��B�Ȃ��A�������������Q�Ƃ��Ă��������B
(1)�ɂ��Ă��������A(3)�ɂ��Ă��������̏��Z�A�����藝���Q�Ƃ��Ă��������B
(1) �w���@�Ŏ����܂��B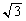 ���L�������Ƃ��āA
���L�������Ƃ��āA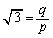 (p�Cq�݂͌��ɑf�Ȏ��R��)�Ƃ������Ɖ��肵�܂��B�������2�悷��ƁA
(p�Cq�݂͌��ɑf�Ȏ��R��)�Ƃ������Ɖ��肵�܂��B�������2�悷��ƁA 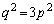 �@����@
�@����@
�E�ӂ�3�̔{���Ȃ̂ŁAq��3�̔{���ł���A

�Ƃ����܂��B�@�ɑ�����A
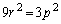 �@��
�@�� 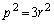 �E�ӂ�3�̔{���Ȃ̂ŁAp��3�̔{���ɂȂ�܂����Ap�Cq���Ƃ���3�̔{���Ƃ������ƂɂȂ�Ap�Cq���݂��ɑf�Ƃ�������Ɩ������܂��B
�E�ӂ�3�̔{���Ȃ̂ŁAp��3�̔{���ɂȂ�܂����Ap�Cq���Ƃ���3�̔{���Ƃ������ƂɂȂ�Ap�Cq���݂��ɑf�Ƃ�������Ɩ������܂��B
����āA ���L�����ł���Ƃ�������͌��ŁA
���L�����ł���Ƃ�������͌��ŁA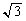 �͖������ł��B(�ؖ��I)
�͖������ł��B(�ؖ��I)
(2) 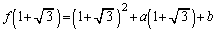
 (1)��p����ƁA
(1)��p����ƁA
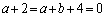
�� 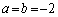 ......[��]
......[��]
(�T) 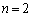 �̂Ƃ��A
�̂Ƃ��A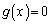 ��2���������ŁA(2)���A
��2���������ŁA(2)���A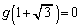 �ƂȂ�L�����W����2���̑������ōō����̌W����1�ƂȂ���̂́A
�ƂȂ�L�����W����2���̑������ōō����̌W����1�ƂȂ���̂́A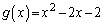 �ƂȂ�܂����A
�ƂȂ�܂����A �́A
�́A �����ɂ��̂ŁA
�����ɂ��̂ŁA �����藧���܂��B
�����藧���܂��B (�U)  �̂Ƃ��A�L�����W����k���������ōō����̌W����1�ƂȂ�
�̂Ƃ��A�L�����W����k���������ōō����̌W����1�ƂȂ�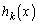 ��
��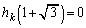 ���݂����Ȃ��
���݂����Ȃ�� �����藧�Ɖ��肵�܂��B
�����藧�Ɖ��肵�܂��B �L�����W���� ���������ōō����̌W����1�ƂȂ�
���������ōō����̌W����1�ƂȂ�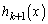 ��
��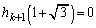 ���݂����Ƃ��āA
���݂����Ƃ��āA
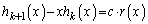 �@����A
�@����A
�Ƃ����܂��B���ӊe���̌W�����r���邱�Ƃɂ��A �͗L�����W����k���̑������ōō����̌W����1�C�L����c��
�͗L�����W����k���̑������ōō����̌W����1�C�L����c�� ��
��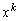 �̌W���ł��B
�̌W���ł��B
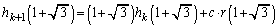
�ł����A ���A
���A
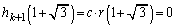
��  �܂���
�܂��� 
(i) 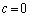 �̂Ƃ��A�A���A
�̂Ƃ��A�A���A (ii) 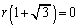 �̂Ƃ��A
�̂Ƃ��A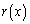 �͗L�����W���ōō����̌W����1��k���̑������Ȃ̂ŁA����ɂ��
�͗L�����W���ōō����̌W����1��k���̑������Ȃ̂ŁA����ɂ��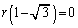 �ł��B����ćA���A
�ł��B����ćA���A ������ɂ��Ă��A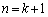 �̂Ƃ���
�̂Ƃ���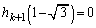 �����藧���܂��B
�����藧���܂��B (�T)�C(�U)���An��2�ȏ�̎��R���A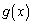 ��L�����W���ōō����̌W����1��n���̑��������Ƃ��āA
��L�����W���ōō����̌W����1��n���̑��������Ƃ��āA �̂Ƃ��A
�̂Ƃ��A �����藧���܂��B
�����藧���܂��B
�NjL�D(3)�ړI�ȕ��@�ōl���Ă݂܂��B
 ���v�Z���邽�߂ɂ́A
���v�Z���邽�߂ɂ́A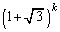 �̌`�̐����l����K�v������܂��B
�̌`�̐����l����K�v������܂��B
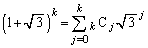 �ł����A������Aj����̍��Ƌ����̍��ɕ����đ������Ƃɂ��A
�ł����A������Aj����̍��Ƌ����̍��ɕ����đ������Ƃɂ��A �Ƃ����`�ɏ������Ƃ��ł��܂��B�܂�A
�Ƃ����`�ɏ������Ƃ��ł��܂��B�܂�A
 �@����B
�@����B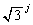 �͎��R���ŁA
�͎��R���ŁA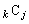 �����R���Ȃ̂ŁA
�����R���Ȃ̂ŁA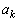 �C
�C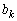 �͎��R���ł��B�܂��A
�͎��R���ł��B�܂��A
���A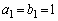 �ł��B
�ł��B
�B�̗��ӂɁA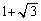 �������āA
�������āA
���A�A���Q�����F
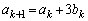 �C
�C �@����C
�@����C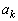 �C
�C �̂ł������炵�āA
�̂ł������炵�āA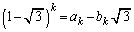 �ł��邱�Ƃ������ł��܂����A
�ł��邱�Ƃ������ł��܂����A
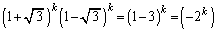 �@����D
�@����D
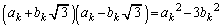 �@����E
�@����E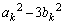 �Ƃ����`�̐�����l���Ă݂�ƁA
�Ƃ����`�̐�����l���Ă݂�ƁA
���A�����F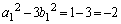 �C����F
�C����F �����䐔���Ȃ̂ŁA
�����䐔���Ȃ̂ŁA
����āA�D�C�E���A
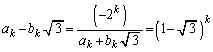 �@����F
�@����F (�A���A
(�A���A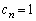 �C
�C �͗L����)�Ƃ��āA�B���A
�͗L����)�Ƃ��āA�B���A
�ł���A(1)���A
�F���A
����Ŏ����܂����B
�y�L���z��������L���ł��B�����̊F���܂̂��x�������������肽���A��낵�����肢�������܂��B
�y�L���z�L���͂����܂łł��B
�@�@���wTOP�@�@TOP�y�[�W�ɖ߂�
�y�L���z��������L���ł��B�����̊F���܂̂��x�������������肽���A��낵�����肢�������܂��B
�y�L���z�L���͂����܂łł��B
�e���̒��쌠��
�o���w�ɑ����܂��B©2005-2024(�L)����� ��w�y�w�m ���������t���I���n��w�l�b�g�m��w�y�w�m(���ē���������)������́A
�܂��A������܂Ń��[����
�����肭�������B 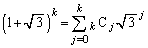 �ł����A������Aj����̍��Ƌ����̍��ɕ����đ������Ƃɂ��A
�ł����A������Aj����̍��Ƌ����̍��ɕ����đ������Ƃɂ��A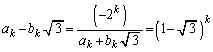 �@����F
�@����F (�A���A
(�A���A