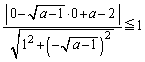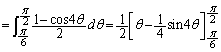��ʑ嗝���w'09�N[3]
xy���ʂɂ�����2�̋Ȑ� �F
�F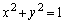 �C
�C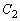 �F
�F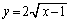 (
(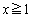 )���l����B���ɁA
)���l����B���ɁA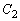 �̓_
�̓_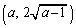 �ɂ�����ڐ���
�ɂ�����ڐ��� �Ƃ���B�������A
�Ƃ���B�������A �̂Ƃ��A�ڐ�
�̂Ƃ��A�ڐ� �͒���
�͒���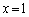 �Ƃ���B
�Ƃ���B
(1) �ڐ� �Ɖ~
�Ɖ~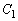 �����L�_�����悤��a�͈̔͂����߂�B
�����L�_�����悤��a�͈̔͂����߂�B (2) a��(1)�ŋ��߂��͈͂ɂ���Ƃ��A�ڐ�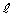 �Ɖ~
�Ɖ~ �̋��L�_��P�CQ�Ƃ���B�������A���L�_��1�_�̏ꍇ��
�̋��L�_��P�CQ�Ƃ���B�������A���L�_��1�_�̏ꍇ��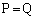 �Ƃ���B���̂Ƃ��A����PQ�̒��_M�̋O��C�̕����������߂�B
�Ƃ���B���̂Ƃ��A����PQ�̒��_M�̋O��C�̕����������߂�B (3) �O��C�Ɖ~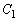 �Ɉ͂܂�A�_
�Ɉ͂܂�A�_ ���܂ސ}�`�̖ʐς����߂�B
���܂ސ}�`�̖ʐς����߂�B
�y�L���z��������L���ł��B�����̊F���܂̂��x�������������肽���A��낵�����肢�������܂��B
�y�L���z�L���͂����܂łł��B
���@(3)�̒�ϕ��v�Z���Ȃ��Ȃ��ʓ|�ł�(�u���ϕ����Q��)�B
(1) 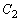 �ɂ��āA
�ɂ��āA 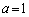 �̂Ƃ��A�ڐ�
�̂Ƃ��A�ڐ� �F
�F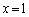 �́A
�́A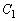 ��̓_
��̓_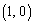 ��ʂ�̂ŁA�ڐ�
��ʂ�̂ŁA�ڐ�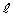 �Ɖ~
�Ɖ~ �͋��L�_�������܂��B
�͋��L�_�������܂��B������A �F
�F �ɑ�����āA
�ɑ�����āA  �������Đ�������ƁA
�������Đ�������ƁA �@����@
�@����@���ӂ� �Ƃ����ƁA�ڐ�
�Ƃ����ƁA�ڐ�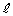 �Ɖ~
�Ɖ~ �����L�_�����Ƃ��A2��������
�����L�_�����Ƃ��A2�������� �́A
�́A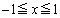 �͈̔͂ɏd�����܂߂�2�������������A���̏���(2���������̉��̔z�u���Q��)�́A
�͈̔͂ɏd�����܂߂�2�������������A���̏���(2���������̉��̔z�u���Q��)�́A ���ʎ��F �@����A
�@����A
���̈ʒu�F �@����B
�@����B
�[�F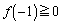 �C
�C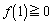 �@����C
�@����C �A���A
�� 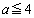 �@����D
�@����D
�B�̍��̕s������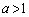 �ł���ΕK���������܂��B�E�̕s�������A
�ł���ΕK���������܂��B�E�̕s�������A 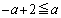 �@��
�@�� 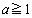 �@����E
�@����E�C�́A
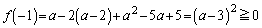 �C
�C
���A�K���������܂��B����āA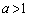 �C�D�C�E���A
�C�D�C�E���A  �̂Ƃ����܂߂āA���L�_������a�͈̔͂́A
�̂Ƃ����܂߂āA���L�_������a�͈̔͂́A ......[��]
......[��]�ʉ��D�~�ƒ����̈ʒu�W���l����ꍇ�ɂ́A�_�ƒ����̋����̌�����p����̂��֗��ł��B
�~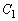 �Ɛڐ�
�Ɛڐ�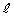 �����L�_�����̂́A�~
�����L�_�����̂́A�~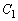 �̒��S
�̒��S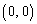 �Ɛڐ�
�Ɛڐ�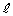 �F
�F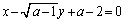 �Ƃ̋��������a1�ȉ��̏ꍇ�ł��B����āA
�Ƃ̋��������a1�ȉ��̏ꍇ�ł��B����āA
(2) P�CQ��x���W��p�Cq�Ƃ��܂��Bp�Cq�͇@��2���ł��B���ƌW���̊W���A PQ�̒��_M��x���WX�́A
a�ɂ��ĉ����ƁA
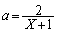 �@����F
�@����F(1)���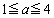 �Ȃ̂ŁA
�Ȃ̂ŁA ��  �@����GM��y���WY�́A�F��
�@����GM��y���WY�́A�F��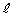 �̎��ɑ�����邱�Ƃɂ��A
�̎��ɑ�����邱�Ƃɂ��A 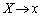 �C
�C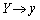 �Ƃ��āAM���O��C�̕������́A
�Ƃ��āAM���O��C�̕������́A ......[��]
......[��]�G���A
 (3) �ʐ�S�����߂�}�`�͉E�}���F���F�����ŁA�~
(3) �ʐ�S�����߂�}�`�͉E�}���F���F�����ŁA�~ ���牺���AC�F
���牺���AC�F ����㑤�̕����ł���A
����㑤�̕����ł���A �̕����ɑ��݂��܂��B
�̕����ɑ��݂��܂��B ���̂����A
���̂����A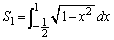 �́A�E�}�̉��ΐF���F�����̖ʐςŁA
�́A�E�}�̉��ΐF���F�����̖ʐςŁA�����̒u�������l���邱�ƂɂȂ�܂����A�Ȃ�ׂ�������ȒP�ɂ������̂ŁA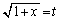 �Ƃ����܂��B
�Ƃ����܂��B �C
�C �C
�C �C
�C �Cx�F
�Cx�F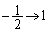 �̂Ƃ��At�F
�̂Ƃ��At�F
�܂��A
�����ŁA��ϕ�����2�ɕ����Čv�Z���܂��B
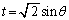 �Ƃ����ƁA
�Ƃ����ƁA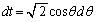 �Ct�F
�Ct�F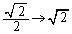 �̂Ƃ��Aθ�F
�̂Ƃ��Aθ�F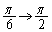
�܂��A �ɂ����āA
�ɂ����āA�� 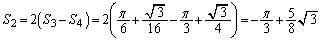 ��
�� 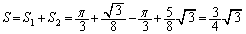 ......[��]
......[��]
�y�L���z��������L���ł��B�����̊F���܂̂��x�������������肽���A��낵�����肢�������܂��B
�y�L���z�L���͂����܂łł��B
�@�@���wTOP�@�@TOP�y�[�W�ɖ߂�
�y�L���z��������L���ł��B�����̊F���܂̂��x�������������肽���A��낵�����肢�������܂��B
�y�L���z�L���͂����܂łł��B
�e���̒��쌠��
�o���w�ɑ����܂��B©2005-2024(�L)����� ��w�y�w�m ���������t���I���n��w�l�b�g�m��w�y�w�m(���ē���������)������́A
�܂��A������܂Ń��[����
�����肭�������B