�����吔�w'10�N[4]
2������\�Ȋ�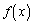 �C���Ȃ킿
�C���Ȃ킿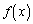 �̓���
�̓���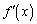 �y��
�y��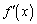 �̓���
�̓���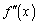 �����݂�������A���ׂĂ̎���x�ɂ���
�����݂�������A���ׂĂ̎���x�ɂ���
�����Ă���B�܂��A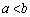 �Ƃ���B
�Ƃ���B
(1) 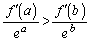 �������B
�������B (2) 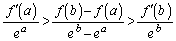 �������B
�������B (3) ���ׂĂ̎���x�ɂ���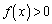 �ł���Ƃ��A���ׂĂ̎���x�ɂ���
�ł���Ƃ��A���ׂĂ̎���x�ɂ��� ���������邱�Ƃ������B
�y�L���z��������L���ł��B�����̊F���܂̂��x�������������肽���A��낵�����肢�������܂��B
�y�L���z�L���͂����܂łł��B
���@(2)�̕s�����̌`����A���ϒl�̒藝������ɂȂ肻���ł��B(3)���Y�݂܂��B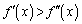 �̈Ӗ����l���Ă݂܂��傤�B
�̈Ӗ����l���Ă݂܂��傤�B
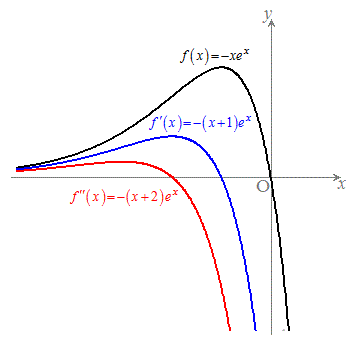 ���Ƃ��āA
���Ƃ��āA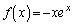 �̂悤�Ȋ����l���Ă݂܂��B
�̂悤�Ȋ����l���Ă݂܂��B
�E�}�̂悤�ɁA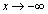 �ł́A
�ł́A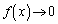 �C
�C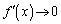 �C
�C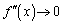 �@(���̋Ɍ����Q��)
�@(���̋Ɍ����Q��)
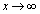 �ł́A
�ł́A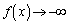 �C
�C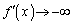 �C
�C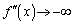
�ƂȂ��Ă��āA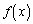 �C
�C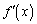 �C
�C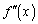 �͓����悤�ȕω������܂��B��L�ł�
�͓����悤�ȕω������܂��B��L�ł�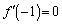 �ł����A�����ŁA
�ł����A�����ŁA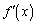 ��
��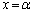 �ɂ�����
�ɂ�����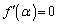 �ɂȂ�Ƃ���ƁA
�ɂȂ�Ƃ���ƁA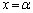 �̑O���
�̑O���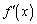 �͐����畉�ɕ�����ς��܂��B�Ƃ������Ƃ́A������
�͐����畉�ɕ�����ς��܂��B�Ƃ������Ƃ́A������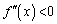 �ł��B
�ł��B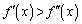 �Ȃ̂ŁA
�Ȃ̂ŁA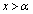 �ɂ�����
�ɂ�����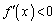 �ł����
�ł����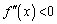 �ł��B
�ł��B
p�����镉�����Ƃ���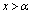 �ɂ�����
�ɂ�����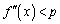 �Ƃ���ƁA
�Ƃ���ƁA
������A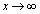 �̂Ƃ�
�̂Ƃ�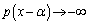 �C
�C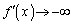 �ƂȂ�܂��B�܂�A
�ƂȂ�܂��B�܂�A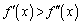 �ł��邽�߂ɁA
�ł��邽�߂ɁA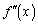 �Ɉ���������
�Ɉ���������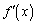 ��
��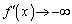 �ƂȂ��Ă��܂��̂ł��B
�ƂȂ��Ă��܂��̂ł��B
���l�ɁA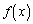 ��
��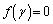 �ƂȂ�悤��γ ������ƁA
�ƂȂ�悤��γ ������ƁA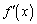 �Ɉ���������
�Ɉ���������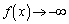 �ƂȂ��Ă��܂��܂��B
�ƂȂ��Ă��܂��܂��B
(3)�ł́A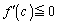 �ƂȂ�c�̑��݂����肷���
�ƂȂ�c�̑��݂����肷���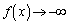 �ƂȂ�
�ƂȂ�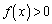 �ɖ������邱�Ƃ���
�ɖ������邱�Ƃ���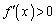 ���������Ƃɂ��܂��B
���������Ƃɂ��܂��B
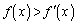 �́A(2)�̕s�����𗘗p���āA���ɁA
�́A(2)�̕s�����𗘗p���āA���ɁA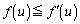 �ƂȂ�u�̑��݂����肷��ƁA
�ƂȂ�u�̑��݂����肷��ƁA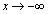 �̂Ƃ�
�̂Ƃ�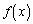 �����l�ɋ߂Â�
�����l�ɋ߂Â�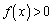 �ɖ������邱�Ƃ���
�ɖ������邱�Ƃ���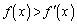 ���������Ƃɂ��܂��B
���������Ƃɂ��܂��B
(1) 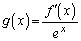 �Ƃ����ƁA
�Ƃ����ƁA
�ƌ��āA
�ƂȂ����c�����݂��邩��A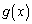 ���P�������ł��邱�Ƃ�p���āA
���P�������ł��邱�Ƃ�p���āA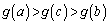 ���A
���A �Ƃ���̂́A���ł��B
�ƂȂ����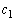 �C
�C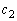 ��
��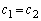 �ƂȂ�Ƃ͌���Ȃ�����ł��B�����ŁA
�ƂȂ�Ƃ͌���Ȃ�����ł��B�����ŁA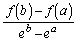 �̌`�̂܂܁A���ϒl�̒藝���g�����Ƃ��l���܂��B
�̌`�̂܂܁A���ϒl�̒藝���g�����Ƃ��l���܂��B
���̂��߂ɁA�u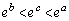 �ƂȂ����c�����݂���v�A�Ƃ����`�ɂ��܂��B
�ƂȂ����c�����݂���v�A�Ƃ����`�ɂ��܂��B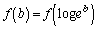 �C
�C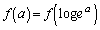 �Ȃ̂ŁA
�Ȃ̂ŁA �Ƃ��������l���܂��B
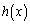 ��
��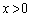 �ɂ����Ĕ����\�Ȋ��Ȃ̂ŁA���ϒl�̒藝���A
�ɂ����Ĕ����\�Ȋ��Ȃ̂ŁA���ϒl�̒藝���A�ƂȂ����c�����݂��܂��B
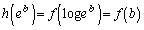 �C
�C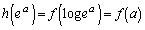 ���A
���A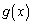 �͒P���������Ȃ̂ŁA
�͒P���������Ȃ̂ŁA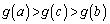 ���A
���A�ʉ��D�ϕ��ɂ���Ă������܂��B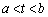 �ƂȂ�t�ɑ��āA(1)�̌��ʂ�p���āA
�ƂȂ�t�ɑ��āA(1)�̌��ʂ�p���āA 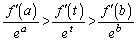 �@����@
�@����@�����̕s�������A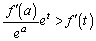
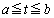 �͈̔͂Őϕ�����ƁA
�͈̔͂Őϕ�����ƁA �� 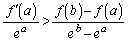 �@�̉E���̕s�������A
�@�̉E���̕s�������A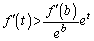
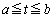 �͈̔͂Őϕ�����ƁA
�͈̔͂Őϕ�����ƁA �� 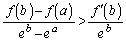
�܂��A�u���ׂĂ�x�ɂ���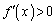 �v��ے肷��ƁA�u�������x�ɂ���
�v��ے肷��ƁA�u�������x�ɂ���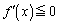 �ɂȂ�v�Ƃ������ƂɂȂ�܂��B�����ŁA
�ɂȂ�v�Ƃ������ƂɂȂ�܂��B�����ŁA
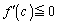 �ƂȂ����c�����݂���A�Ɖ��肵�܂��B
�ƂȂ����c�����݂���A�Ɖ��肵�܂��B
���ϒl�̒藝���A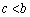 �̂Ƃ�(���Ƃ�
�̂Ƃ�(���Ƃ�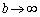 �Ƃ���̂ŁAc�����傫��b���l���܂�)�A
�Ƃ���̂ŁAc�����傫��b���l���܂�)�A 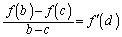 �C
�C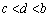 �@����A
�@����A�ƂȂ����d�����݂��܂��B���̂Ƃ��A(1)�̌��ʂ�p���āA
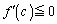 ���A
���A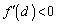 �ł��B�A���A
�ł��B�A���A�����ŁA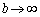 �Ƃ���ƁA
�Ƃ���ƁA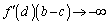 �C
�C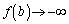 �@(�͂��݂����̌������Q��)����́A�u���ׂĂ̎����ɂ���
�@(�͂��݂����̌������Q��)����́A�u���ׂĂ̎����ɂ���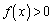 �v�ɖ������܂��B�]���āA�u
�v�ɖ������܂��B�]���āA�u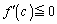 �ƂȂ����c�����݂���v�Ƃ�������͌��ŁA���ׂĂ̎���x�ɂ���
�ƂȂ����c�����݂���v�Ƃ�������͌��ŁA���ׂĂ̎���x�ɂ���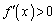 �@����B
�@����B
�u���ׂĂ̎���x�ɂ���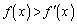 �v��ے肷�邽�߂ɁA
�v��ے肷�邽�߂ɁA �Ƃ��������l���܂��B
���A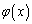 �͒P���������ł��B
�͒P���������ł��B
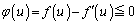 �ƂȂ����u�����݂���Ɖ��肵�܂��B
�ƂȂ����u�����݂���Ɖ��肵�܂��B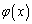 �͒P�������Ȃ̂ŁA
�͒P�������Ȃ̂ŁA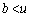 �̂Ƃ��A
�̂Ƃ��A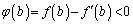 (2)�̌��ʂ̉E���̕s�����ɂ��āA
(2)�̌��ʂ̉E���̕s�����ɂ��āA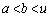 �̂Ƃ�(���Ƃ�
�̂Ƃ�(���Ƃ�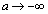 �Ƃ���̂ŁAu����������a�Cb���l���܂�)�A
�Ƃ���̂ŁAu����������a�Cb���l���܂�)�A 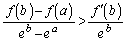
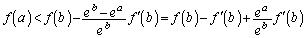 �@����C
�@����C�����ŁA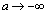 �Ƃ���ƁA
�Ƃ���ƁA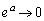 �C
�C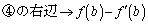 (
(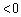 ) �ƂȂ�A
) �ƂȂ�A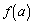 �́A���镉�̒l�ɋ߂Â����A���邢�́A���̖�����ɔ��U���A�u���ׂĂ̎����ɂ���
�́A���镉�̒l�ɋ߂Â����A���邢�́A���̖�����ɔ��U���A�u���ׂĂ̎����ɂ���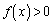 �v�Ɩ������܂��B�]���āA�u
�v�Ɩ������܂��B�]���āA�u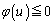 �ƂȂ����u�����݂���v�Ƃ�������͌��ŁA���ׂĂ̎���x�ɂ���
�ƂȂ����u�����݂���v�Ƃ�������͌��ŁA���ׂĂ̎���x�ɂ���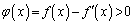 �C�܂�A
�C�܂�A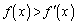 �@����D
�@����D �B�C�D���A���ׂĂ̎���x�ɂ��āA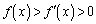
�y�L���z��������L���ł��B�����̊F���܂̂��x�������������肽���A��낵�����肢�������܂��B
�y�L���z�L���͂����܂łł��B
�@�@���wTOP�@�@TOP�y�[�W�ɖ߂�
�y�L���z��������L���ł��B�����̊F���܂̂��x�������������肽���A��낵�����肢�������܂��B
�y�L���z�L���͂����܂łł��B
�e���̒��쌠��
�o���w�ɑ����܂��B©2005-2024(�L)����� ��w�y�w�m ���������t���I���n��w�l�b�g�m��w�y�w�m(���ē���������)������́A
�܂��A������܂Ń��[����
�����肭�������B