��嗝�n���w'24�N�O��[1]
���R��n�ɑ��āA��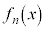 ��
��
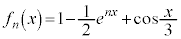 �@(
�@(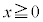 )
)
(1) ������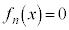 �́A����1�̎������������Ƃ������B
�́A����1�̎������������Ƃ������B (2) (1)�ɂ������������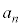 �Ƃ����Ƃ��A�Ɍ��l
�Ƃ����Ƃ��A�Ɍ��l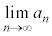 �����߂�B
�����߂�B (3) �Ɍ��l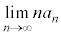 �����߂�B
�����߂�B
�y�L���z��������L���ł��B�����̊F���܂̂��x�������������肽���A��낵�����肢�������܂��B
�y�L���z�L���͂����܂łł��B
���@���Ԓl�̒藝��p����������̉��̑��݂̏ؖ��A�͂��݂����̌�����p����Ɍ��A������ɂ����Ă����̓T�^���ł��B���ʂ��������ł��B
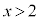 �̂Ƃ��A
�̂Ƃ��A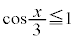 ���A
���A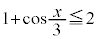 �@����An�����R�����A
�@����An�����R�����A
�����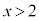 �̂Ƃ��A
�̂Ƃ��A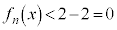 �@����B
�@����B
����Ƈ@���A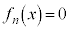 �͘A���Ȋ��Ȃ̂ŁA������
�͘A���Ȋ��Ȃ̂ŁA������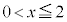 �́A
�́A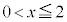 �͈̔͂Ŏ������������܂��B
�͈̔͂Ŏ������������܂��B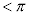 (
(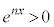 )�ɂ����āA
)�ɂ����āA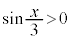 �C
�C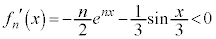
����āA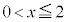 ��
��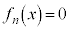 �ɂ������P�������ł��B����ƁA�@�C�B�C���Ԓl�̒藝���A������
�ɂ������P�������ł��B����ƁA�@�C�B�C���Ԓl�̒藝���A������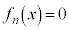 �́A����1�̎������������܂��B
�́A����1�̎������������܂��B
(2) ������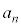 �̉���
�̉���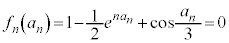 �ł��邱�Ƃ���A
�ł��邱�Ƃ���A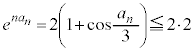
�A���A
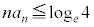 �@����C
�@����C�� 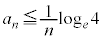 �C
�C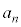 �@����D(1)���A
�@����D(1)���A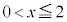 ��
��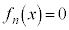 �ɂ����������
�ɂ����������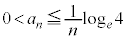 �̉��Ȃ̂ŁA�D���
�̉��Ȃ̂ŁA�D���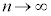 �C
�C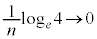 �Ƃ���ƁA
�Ƃ���ƁA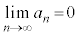 (����̋Ɍ����Q��)�C�͂��݂����̌������A
(����̋Ɍ����Q��)�C�͂��݂����̌������A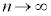 ......[��]
......[��]
(3) �C�ɂ����āA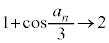 �̂Ƃ��A(2)�̌��ʂ��A
�̂Ƃ��A(2)�̌��ʂ��A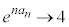
�y�L���z��������L���ł��B�����̊F���܂̂��x�������������肽���A��낵�����肢�������܂��B
�y�L���z�L���͂����܂łł��B
�@�@���wTOP�@�@TOP�y�[�W�ɖ߂�
�y�L���z��������L���ł��B�����̊F���܂̂��x�������������肽���A��낵�����肢�������܂��B
�y�L���z�L���͂����܂łł��B
�e���̒��쌠��
�o���w�ɑ����܂��B©2005-2024(�L)����� ��w�y�w�m ���������t���I���n��w�l�b�g�m��w�y�w�m(���ē���������)������́A
�܂��A������܂Ń��[����
�����肭�������B 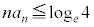 �@����C
�@����C