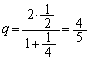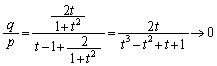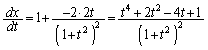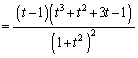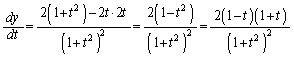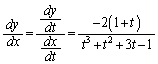�c�嗝�H���w'08�N[A4]
(1) t�������Ƃ���B���W���ʓ���2�_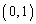 �C
�C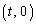 �����Ԑ����̐���2������
�����Ԑ����̐���2������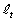 �̌X�����@�e�@�ŁA��������y���@�e�@x�{�@�g�@�ł���B
�̌X�����@�e�@�ŁA��������y���@�e�@x�{�@�g�@�ł���B ����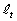 �Ɋւ��ē_
�Ɋւ��ē_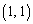 �ƑΏ̂Ȉʒu�ɂ���_��
�ƑΏ̂Ȉʒu�ɂ���_��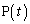 �Ƃ���B���W�ł���킷�ƁA
�Ƃ���B���W�ł���킷�ƁA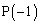 ��
��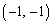 �C
�C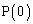 ���@�i�@�C
���@�i�@�C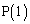 ���@�j�@�ł���B�܂�
���@�j�@�ł���B�܂�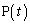 �̍��W��t��p���Ă���킷��
�̍��W��t��p���Ă���킷��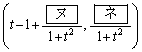 �ł���B
�ł���B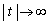 �̂Ƃ�
�̂Ƃ�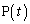 �͒���y���@�m�@�Ɍ���Ȃ��߂Â��B
�͒���y���@�m�@�Ɍ���Ȃ��߂Â��B (2) t�����ׂĂ̎������Ƃ�Ƃ���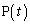 ���`���Ȑ���C�Ƃ���B�_
���`���Ȑ���C�Ƃ���B�_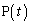 (
(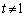 )�ɂ�����C�̐ڐ��̌X���́A
)�ɂ�����C�̐ڐ��̌X���́A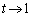 �̂Ƃ��@�n�@�ɋ߂Â��B�Ȑ�C�ƒ���
�̂Ƃ��@�n�@�ɋ߂Â��B�Ȑ�C�ƒ���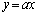 ���قȂ�3�_�Ō���邽�߂̕K�v�\���������@�q�@ �� a �� �@�t�@�ł���B
���قȂ�3�_�Ō���邽�߂̕K�v�\���������@�q�@ �� a �� �@�t�@�ł���B
�y�L���z��������L���ł��B�����̊F���܂̂��x�������������肽���A��낵�����肢�������܂��B
�y�L���z�L���͂����܂łł��B
���@�u�K�v�\�������v�Ə�����Ă��邩��A��������ؖ����Ă����Ȃ����(�q)(�t)�̉������Ă͂Ȃ�Ȃ��Ǝv������ł��܂��ƁA�u���i�v�������Ȃ��Ă��܂��܂��B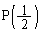 ���炢�ׂ�A�Ȑ�C�̑�̂̎p�͂킩��̂ŁA������ł́A��X����������(�n)(�q)(�t)�߂Ă��܂��̂��������Ǝv���܂��B
���炢�ׂ�A�Ȑ�C�̑�̂̎p�͂킩��̂ŁA������ł́A��X����������(�n)(�q)(�t)�߂Ă��܂��̂��������Ǝv���܂��B
(1)(�e) 2�_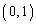 �C
�C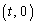 �����Ԑ����̌X���́A
�����Ԑ����̌X���́A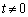 �̂Ƃ��A
�̂Ƃ��A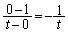 �C
�C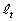 �̌X����t ......[��]�@(
�̌X����t ......[��]�@(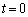 �̂Ƃ�������ł悢)
�̂Ƃ�������ł悢) (�g) 2�_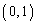 �C
�C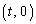 �̒��_�́A
�̒��_�́A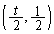 �C���̓_��ʂ��āA�X��t�̒���
�C���̓_��ʂ��āA�X��t�̒���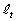 �́A
�́A 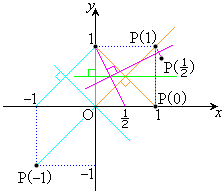 (�i)
(�i) 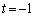 �̂Ƃ��A
�̂Ƃ��A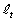 �F
�F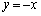 �ƂȂ�̂ŁA
�ƂȂ�̂ŁA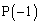 �́A
�́A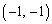 �ɂȂ�܂�(�E�}���F)�B
�ɂȂ�܂�(�E�}���F)�B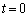 �̂Ƃ��A
�̂Ƃ��A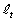 �F
�F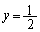
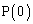 �́A
�́A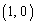 ......[��]�@(�E�}���ΐF)
......[��]�@(�E�}���ΐF)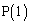 �́A
�́A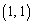 ......[��]�@ (�E�}��F)
......[��]�@ (�E�}��F)����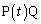 ��
��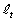 �������F
�������F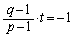 �@����@
�@����@
����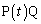 �̒��_��
�̒��_��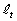 ��F
��F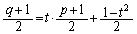 �@����A
�@����A
�@���A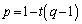 �@����B
�@����B
�A�ɑ�����āA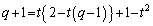
�� 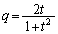 �B�ɑ�����āA
�B�ɑ�����āA ����āA(�k)�́A2�C(�l)�́A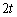 ......[��]������ł́A
......[��]������ł́A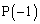 ��
��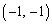 �C
�C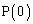 ��
��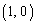 �C
�C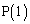 ��
��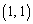 �ƂȂ邱�Ƃ��m�F���Ă��������B����ƁA
�ƂȂ邱�Ƃ��m�F���Ă��������B����ƁA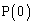 ��
��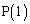 ��x���W�͂Ƃ���1�ł��B
��x���W�͂Ƃ���1�ł��B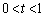 �̂Ƃ�
�̂Ƃ�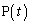 ���ǂ��ɍs���Ă��܂��̂��A�Ƃ������Ƃ��C�ɂȂ�܂��B
���ǂ��ɍs���Ă��܂��̂��A�Ƃ������Ƃ��C�ɂȂ�܂��B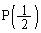 ���m�F���܂��傤�B
���m�F���܂��傤�B
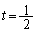 �̂Ƃ��A
�̂Ƃ��A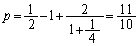 �C
�C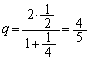
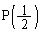 �́A
�́A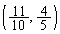 �ł��B
�ł��B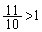 �Ȃ̂ŁA
�Ȃ̂ŁA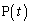 �̋O�Ղ́A
�̋O�Ղ́A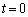 �̂Ƃ���
�̂Ƃ���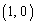 ��ʉ߂�����A��U�A
��ʉ߂�����A��U�A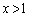 �̕����ɏo�������Ă���A
�̕����ɏo�������Ă���A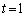 �̂Ƃ���
�̂Ƃ���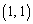 �܂ň����Ԃ��Ă���炵���A�Ƃ������Ƃ����߂܂��B���(��)
�܂ň����Ԃ��Ă���炵���A�Ƃ������Ƃ����߂܂��B���(��) (�m) 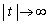 �̂Ƃ�
�̂Ƃ�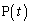 ���߂Â������A�Ƃ����̂́A�Q�ߐ��̂��Ƃł����A
���߂Â������A�Ƃ����̂́A�Q�ߐ��̂��Ƃł����A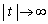 �̂Ƃ��A
�̂Ƃ��A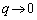 �Ƃ��������ŁA(�m)��0�Ƃ��Ă��܂��Ă��ǂ��Ǝv���܂��B
�Ƃ��������ŁA(�m)��0�Ƃ��Ă��܂��Ă��ǂ��Ǝv���܂��B ������Ɗm�F����̂Ȃ�A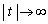 �̂Ƃ��A
�̂Ƃ��A ���A�Q�ߐ��̌X����0 (���́A�̌`����킩���Ă��܂�)�ŁA
���A�Q�ߐ���y�ؕЂ�0����āA�Q�ߐ���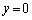 ......[��]�Q�ߐ���x���ł��邱�ƂƁA(��)����A(2)��(�n)(�q)(�t)�͔����v�Z���Ȃ��Ă��A�����킩���Ă��܂��܂��B�����v�Z������Ă��܂��Ǝ��ԓI���X���傫���Ȃ�̂ŁA������ł͏[���ɒ��ӂ��Ă��������B
......[��]�Q�ߐ���x���ł��邱�ƂƁA(��)����A(2)��(�n)(�q)(�t)�͔����v�Z���Ȃ��Ă��A�����킩���Ă��܂��܂��B�����v�Z������Ă��܂��Ǝ��ԓI���X���傫���Ȃ�̂ŁA������ł͏[���ɒ��ӂ��Ă��������B 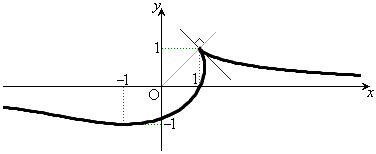 (2)(�n) ������ł͈ȉ��̂悤�ɂ���̂����p�I�ł��B
(2)(�n) ������ł͈ȉ��̂悤�ɂ���̂����p�I�ł��B
(1)����Ȑ�C�́A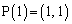 �łƂ����Ă���(��_�ƌ����܂�)�A
�łƂ����Ă���(��_�ƌ����܂�)�A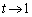 �̂Ƃ��̐ڐ��́A
�̂Ƃ��̐ڐ��́A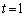 �̂Ƃ���
�̂Ƃ���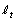 (�X���F1)�ɐ����ɂȂ肻���ł��B�]���āA�ڐ��̌X���́A
(�X���F1)�ɐ����ɂȂ肻���ł��B�]���āA�ڐ��̌X���́A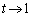 �̂Ƃ��A
�̂Ƃ��A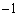 ......[��]�@�ɋ߂Â����Ƃ��킩��܂��B
......[��]�@�ɋ߂Â����Ƃ��킩��܂��B (�q�t)����ŁA�Ȑ�C�̊T�`���E�}�̂悤�ɂȂ邱�Ƃ��킩���Ă��܂��̂ŁA�Ȑ�C�ƒ���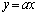 ���قȂ�3�_�Ō���邽�߂��K�v�\�������́A
���قȂ�3�_�Ō���邽�߂��K�v�\�������́A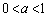
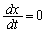 �Ƃ���ƁA
�Ƃ���ƁA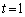 �C�܂��́A
�C�܂��́A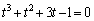
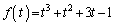 �Ƃ����ƁA
�Ƃ����ƁA���A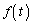 �͒P�������Ȋ�(3�����̑������Q��)�ŁA
�͒P�������Ȋ�(3�����̑������Q��)�ŁA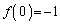 �C
�C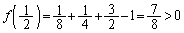 ���A������
���A������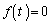 ��
��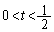 �͈̔͂ɉ��������Ă��܂��B�����α�Ƃ��܂��B�����\���(���̑������Q��)�At��
�͈̔͂ɉ��������Ă��܂��B�����α�Ƃ��܂��B�����\���(���̑������Q��)�At��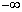 ���玟��ɑ傫�����Ă���ƁA����ɔ�����x�́A
���玟��ɑ傫�����Ă���ƁA����ɔ�����x�́A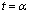 �܂ł͑��債�A�Ȑ��͍�����E�ɐi�݂܂����A
�܂ł͑��債�A�Ȑ��͍�����E�ɐi�݂܂����A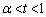 �ɂ����Ă�x�͌������A�Ȑ��́A�E���獶�Ɉ����Ԃ������ɂȂ�܂��B
�ɂ����Ă�x�͌������A�Ȑ��́A�E���獶�Ɉ����Ԃ������ɂȂ�܂��B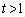 �ɂ����Ă�x�͑��債�A�ĂсA������E�ɐi�݂܂��B
�ɂ����Ă�x�͑��債�A�ĂсA������E�ɐi�݂܂��B 2�̑����\����O���t�̊T�`�͉E��}�̂悤�ɂȂ�܂��B
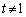 �ɂ����āA
�ɂ����āA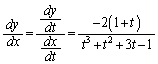
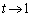 �̂Ƃ��A
�̂Ƃ��A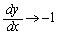 ���A(�n)��
���A(�n)��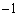
�O���t�̊T�`���A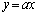 �͋Ȑ�C��(�����@�̕������ւ̉��p(2)���Q��)�A
�͋Ȑ�C��(�����@�̕������ւ̉��p(2)���Q��)�A
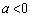 �̂Ƃ��A��4�ی��ł̂�1��_�������A
�̂Ƃ��A��4�ی��ł̂�1��_�������A
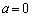 �̂Ƃ��A1��_
�̂Ƃ��A1��_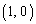 �������A
�������A
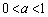 �̂Ƃ��A��3�ی���1��_�A��1�ی��ŁA�Ȑ���
�̂Ƃ��A��3�ی���1��_�A��1�ی��ŁA�Ȑ���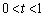 �̕����A�܂��A�Ȑ���
�̕����A�܂��A�Ȑ���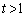 �̕����ŁA�v3��_�������A
�̕����ŁA�v3��_�������A
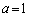 �̂Ƃ��A��3�ی���1��_�A��1�ی���1��_
�̂Ƃ��A��3�ی���1��_�A��1�ی���1��_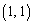 �C���킹�āA2��_�������A
�C���킹�āA2��_�������A
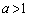 �̂Ƃ��A��3�ی���1��_�����A
�̂Ƃ��A��3�ی���1��_�����A
�]���āA�Ȑ�C�ƒ���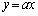 ���قȂ�3�_�Ō���邽�߂��K�v�\�������́A
���قȂ�3�_�Ō���邽�߂��K�v�\�������́A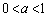
����ŁA(�q)��0�C(�t)��1�C�Ƃ������ƂɂȂ�܂��B
�y�L���z��������L���ł��B�����̊F���܂̂��x�������������肽���A��낵�����肢�������܂��B
�y�L���z�L���͂����܂łł��B
�@�@�c�嗝�H���wTOP�@�@���wTOP�@�@TOP�y�[�W�ɖ߂�
�y�L���z��������L���ł��B�����̊F���܂̂��x�������������肽���A��낵�����肢�������܂��B
�y�L���z�L���͂����܂łł��B
�e���̒��쌠��
�o���w�ɑ����܂��B©2005-2024(�L)����� ��w�y�w�m ���������t���I���n��w�l�b�g�m��w�y�w�m(���ē���������)������́A
�܂��A������܂Ń��[����
�����肭�������B  �ł���B
�ł���B