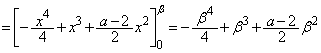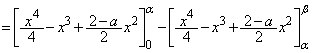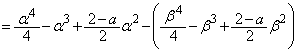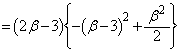���H�吔�w'12�N�O��[3]
3����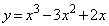 �̃O���t��C�C����
�̃O���t��C�C����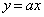 ��l�Ƃ���B
��l�Ƃ���B
(1) C��l�����_�ȊO�̋��L�_�����悤�Ȏ���a�͈̔͂����߂�B
(2) a��(1)�ŋ��߂��͈͓��ɂ���Ƃ��AC��l�ɂ���Ĉ͂܂�镔���̖ʐς�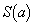 �Ƃ���B
�Ƃ���B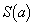 ���ŏ��ƂȂ�a�̒l�����߂�B
���ŏ��ƂȂ�a�̒l�����߂�B
�y�L���z��������L���ł��B�����̊F���܂̂��x�������������肽���A��낵�����肢�������܂��B
�y�L���z�L���͂����܂łł��B
���@���ƌW���̊W�𗘗p����Ƃ��Ă��A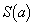 ��a�̊��Ƃ���̂ł͕��G�ɂȂ�̂ŁA���Ȃ�ʓ|�ł��B
��a�̊��Ƃ���̂ł͕��G�ɂȂ�̂ŁA���Ȃ�ʓ|�ł��B
C�F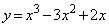 �@����@
�@����@
l�F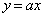 �@����A
�@����A
(1) �@�C�A��A�����āA
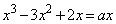
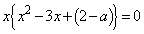 �@����B
�@����B���_�ȊO�̋��L�_�����Ƃ��A���̕������́A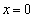 �ȊO�̉��������܂��B�܂�A2���������A
�ȊO�̉��������܂��B�܂�A2���������A 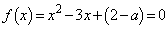 �@����C
�@����C���A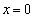 ���d���Ƃ��邱�Ƃ��Ȃ��A�܂��́A���قȂ�2�������������܂��B
���d���Ƃ��邱�Ƃ��Ȃ��A�܂��́A���قȂ�2�������������܂��B
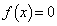 ��
��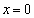 �����ɂ��Ƃ��A
�����ɂ��Ƃ��A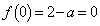 ���
���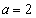 �ł����A���̂Ƃ��A
�ł����A���̂Ƃ��A ���A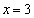 �����ɂȂ�̂ŁAC��l�͌��_�ȊO�̋��L�_�������܂��B
�����ɂȂ�̂ŁAC��l�͌��_�ȊO�̋��L�_�������܂��B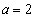 �̂Ƃ��A3���������B�́A
�̂Ƃ��A3���������B�́A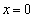 ���d���ɂ��̂ŁAC��l�́A
���d���ɂ��̂ŁAC��l�́A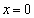 �Őڂ��A
�Őڂ��A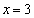 �Ō����܂��B�@����D2���������C�����قȂ�����������Ƃ��A
�Ō����܂��B�@����D2���������C�����قȂ�����������Ƃ��A �� 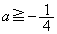 �ȏ���AC��l�����_�ȊO�̋��L�_�����悤�Ȏ���a�͈̔͂́A
�ȏ���AC��l�����_�ȊO�̋��L�_�����悤�Ȏ���a�͈̔͂́A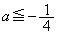 ......[��]
......[��]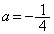 �̂Ƃ��A�C�́A�d��
�̂Ƃ��A�C�́A�d��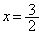 �������܂��B�@����E
�������܂��B�@����E
(2) 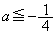 �̂Ƃ��A2���������C��2��������α�Cβ �Ƃ��āA���ƌW���̊W���A
�̂Ƃ��A2���������C��2��������α�Cβ �Ƃ��āA���ƌW���̊W���A 2���������C�́A(i) 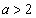 �̂Ƃ��A
�̂Ƃ��A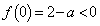 ���A�C�͐���2���������܂��B�@(ii)
���A�C�͐���2���������܂��B�@(ii) 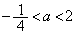 �̂Ƃ��A
�̂Ƃ��A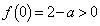 ���
���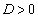 �ƍ��킹�āA�C�͐��̉�2���������܂��B
�ƍ��킹�āA�C�͐��̉�2���������܂��B (i) 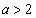 �̂Ƃ��A�C�̐��̉���β �Ƃ��āA
�̂Ƃ��A�C�̐��̉���β �Ƃ��āA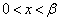 �ɂ�����l��C�̏�ɗ���̂ŁAC��l�ɂ���Ĉ͂܂�镔�����ʐ��́A
�ɂ�����l��C�̏�ɗ���̂ŁAC��l�ɂ���Ĉ͂܂�镔�����ʐ��́A �����ŁAβ ��a��p���ĕ\����悢�̂ł����A�F��p����ƍ������܂ޕ��G�Ȏ��ɂȂ��Ă��܂��܂��B
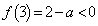 ���
���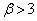 (�D�ɒ���)�Ȃ̂ŁA
(�D�ɒ���)�Ȃ̂ŁA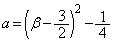 �́Aβ ���������ŁA�܂��Aβ ��a�̑������ł��B�����ŁA�F��p���āA
�́Aβ ���������ŁA�܂��Aβ ��a�̑������ł��B�����ŁA�F��p���āA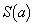 ��β �̊��ƍl���邱�Ƃɂ��܂��B
��β �̊��ƍl���邱�Ƃɂ��܂��B �Ƃ����ƁA
���A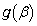 ��β �̑������ł��B
��β �̑������ł��B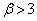 �ɂ����ẮA
�ɂ����ẮA 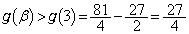 �@����G
�@����G(ii) 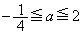 �̂Ƃ��A�C�̐��̉�2����α�Cβ (
�̂Ƃ��A�C�̐��̉�2����α�Cβ (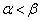 )�Ƃ��܂��B�F�����藧���܂��B
)�Ƃ��܂��B�F�����藧���܂��B ���̂Ƃ��A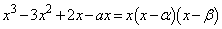 �́A
�́A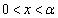 �ɂ����Đ���C��l�̏�ɂ���A
�ɂ����Đ���C��l�̏�ɂ���A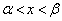 �ɂ����ĕ���l��C�̏�ɂ���̂ŁA
�ɂ����ĕ���l��C�̏�ɂ���̂ŁA �Ƃ����܂��B(i)�Ɠ��l�ɁA�C��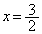 �Ƃ���(�E�ɒ���)�A
�Ƃ���(�E�ɒ���)�A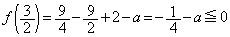 ���A
���A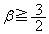 (
(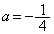 �ŏd���̏ꍇ�́A
�ŏd���̏ꍇ�́A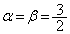 )�Ȃ̂ŁA
)�Ȃ̂ŁA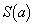 ��β �̊��Ƃ��čl���܂��B���̏ꍇ���A
��β �̊��Ƃ��čl���܂��B���̏ꍇ���A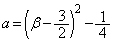 �́Aβ �̑������ŁAβ ��a�̑������ł��B�܂��A
�́Aβ �̑������ŁAβ ��a�̑������ł��B�܂��A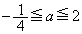 �̂Ƃ��A
�̂Ƃ��A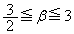 �ł��B
�ł��B 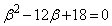 �Ƃ���ƁA
�Ƃ���ƁA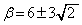
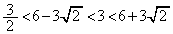 ���A�����\�́A
���A�����\�́A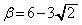 �̂Ƃ��A
�̂Ƃ��A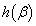 �ŏ��ł��B
�ŏ��ł��B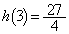 �ƇG�Ƃ���A
�ƇG�Ƃ���A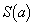 �́A
�́A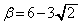 �̂Ƃ��ŏ��ŁA���̂Ƃ��A
�̂Ƃ��ŏ��ŁA���̂Ƃ��A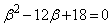 ���A�F��p���āA
���A�F��p���āA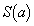 ���ŏ��ƂȂ�a�́A
���ŏ��ƂȂ�a�́A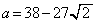 ......[��]
......[��]
�y�L���z��������L���ł��B�����̊F���܂̂��x�������������肽���A��낵�����肢�������܂��B
�y�L���z�L���͂����܂łł��B
�@�@���H�吔�wTOP�@�@���wTOP�@�@TOP�y�[�W�ɖ߂�
�y�L���z��������L���ł��B�����̊F���܂̂��x�������������肽���A��낵�����肢�������܂��B
�y�L���z�L���͂����܂łł��B
�e���̒��쌠��
�o���w�ɑ����܂��B©2005-2024(�L)����� ��w�y�w�m ���������t���I���n��w�l�b�g�m��w�y�w�m(���ē���������)������́A
�܂��A������܂Ń��[����
�����肭�������B