���H�吔�w'22�N�O��[1]
a�Cb�������Ƃ��A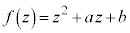 �Ƃ���Ba�Cb��
�Ƃ���Ba�Cb��
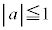 �C
�C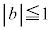
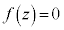 �������f��z���Ƃ肤��l�͈̔͂f�����ʏ�ɐ}������B
�������f��z���Ƃ肤��l�͈̔͂f�����ʏ�ɐ}������B
�y�L���z��������L���ł��B�����̊F���܂̂��x�������������肽���A��낵�����肢�������܂��B
�y�L���z�L���͂����܂łł��B
���@���f��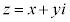 ������x�Ƌ���y�ɕ����Aa�Cb��x�Cy�ŕ\����
������x�Ƌ���y�ɕ����Aa�Cb��x�Cy�ŕ\����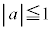 �C
�C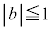 �ɑ�����邩�A2��������
�ɑ�����邩�A2��������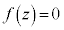 �̉����l���邩�A�ł����A2�ʂ�̃A�v���[�`�ł���Ă݂܂��B
�̉����l���邩�A�ł����A2�ʂ�̃A�v���[�`�ł���Ă݂܂��B
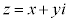 (x�Cy�͎���)�Ƃ����ƁA
(x�Cy�͎���)�Ƃ����ƁA
(i) 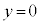 �̂Ƃ��A�A�͕K���������܂��B
�̂Ƃ��A�A�͕K���������܂��B �@���A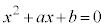
�����ab���ʏ�̒���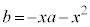 �ƌ���ƁA���̒������A
�ƌ���ƁA���̒������A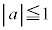 �C
�C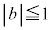 �ŕ\�����̈��ʉ߂������(���`�v��@���Q��)�́A
�ŕ\�����̈��ʉ߂������(���`�v��@���Q��)�́A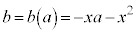 �Ƃ���
�Ƃ���
�E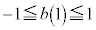 �܂���
�܂���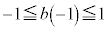 �@����B
�@����B
�܂���
�E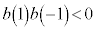 �@����C
�@����C
���������邱�Ƃł�(�ȉ��A2���s�������Q��)�B
�C���A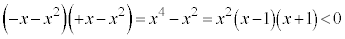
�� 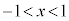 �@����D
�@����D
�B���A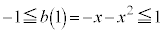
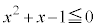 ����
����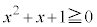
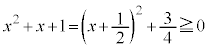 �͕K���������܂��B
�͕K���������܂��B
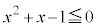 ���A
���A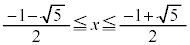 �@����E
�@����E
�B���A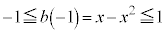
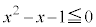 ����
����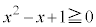
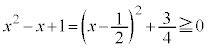 �͕K���������܂��B
�͕K���������܂��B
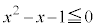 ���A
���A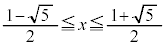 �@����F
�@����F
�E�܂��͇F����������悢(�E���F�ł͂Ȃ��̂Œ���)�̂ŁA 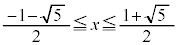 �@����G
�@����G����͇D�͈̔͂��܂ނ̂ŇG�����l�����OK�ł��B
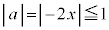 ���A
���A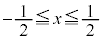 �@����H
�@����H
�@��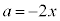 �Ƃ��āA
�Ƃ��āA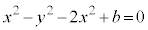
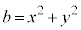 ��
��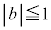 ���A
���A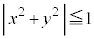
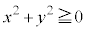 ���A
���A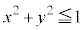 �@����I
�@����I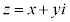 �̑��ݔ͈�(�s�����̕\���̈����Q��)�́A"
�̑��ݔ͈�(�s�����̕\���̈����Q��)�́A"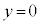 ���G"�܂���"
���G"�܂���"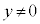 ���H���I"�ł��B�}������ƁA�E�}���ΐF���F��(���E���Ƒ������܂�)�B
���H���I"�ł��B�}������ƁA�E�}���ΐF���F��(���E���Ƒ������܂�)�B
[�ʉ�]�@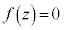 �̉����l���Ă��ł��܂�(2�����������Q��)�B
�̉����l���Ă��ł��܂�(2�����������Q��)�B
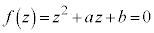 �@����J
�@����J(i) 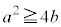 �̂Ƃ��J�͎������������A
�̂Ƃ��J�͎������������A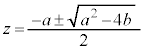 (����)
(����) 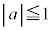 �C
�C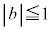 ���A
���A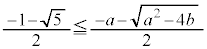 �C
�C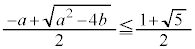
����āA���̂Ƃ���z�̑��ݔ͈͂́A��������̕����ł��B
(ii) 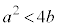 �̂Ƃ��J�͋������������A
�̂Ƃ��J�͋������������A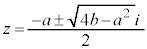
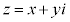 (x�Cy�͎���)�Ƃ���ƁA
(x�Cy�͎���)�Ƃ���ƁA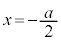 �C
�C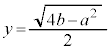
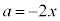 �C
�C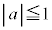 ���
���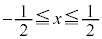
�܂��A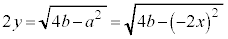 ���A
���A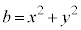
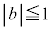 ���A
���A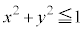
���߂�̈��(i)�̌��ʂ�(ii)�̌��ʂ����킹���̈�ł��B
�y�L���z��������L���ł��B�����̊F���܂̂��x�������������肽���A��낵�����肢�������܂��B
�y�L���z�L���͂����܂łł��B
�@�@���H�吔�wTOP�@�@���wTOP�@�@TOP�y�[�W�ɖ߂�
�y�L���z��������L���ł��B�����̊F���܂̂��x�������������肽���A��낵�����肢�������܂��B
�y�L���z�L���͂����܂łł��B
�e���̒��쌠��
�o���w�ɑ����܂��B©2005-2024(�L)����� ��w�y�w�m ���������t���I���n��w�l�b�g�m��w�y�w�m(���ē���������)������́A
�܂��A������܂Ń��[����
�����肭�������B