���嗝�n���w'05�N�O��[2]
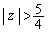 �ƂȂ�ǂ̂悤�ȕ��f��z�ɑ��Ă�
�ƂȂ�ǂ̂悤�ȕ��f��z�ɑ��Ă�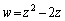 �Ƃ͕\����Ȃ����f��w�S�̂̏W����T�Ƃ���B���Ȃ킿�A
�Ƃ͕\����Ȃ����f��w�S�̂̏W����T�Ƃ���B���Ȃ킿�A
�Ƃ���B���̂Ƃ��AT�ɑ����镡�f��w�Ő�Βl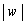 ���ő�ɂȂ�悤��w�̒l�����߂�B
���ő�ɂȂ�悤��w�̒l�����߂�B
�y�L���z��������L���ł��B�����̊F���܂̂��x�������������肽���A��낵�����肢�������܂��B
�y�L���z�L���͂����܂łł��B
���@��蕶�O���̌������ł́A�l���ɂ����̂ŁA�W���L�@�ŏ��������Ă�����ōl���邱�Ƃɂ��܂��B
�܂��A�ϊ����F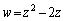 ��z��2���������F
��z��2���������F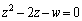 ����@ �ƌ��āAz�ɂ��ĉ����܂��B
����@ �ƌ��āAz�ɂ��ĉ����܂��B
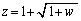 ����A
����A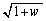 ��2�悵��
��2�悵��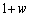 �ɂȂ镡�f�����Ƃ��܂��B
�ɂȂ镡�f�����Ƃ��܂��B
�ł�������ł́A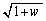 �̏��u�ɍ���܂��B2�悵��
�̏��u�ɍ���܂��B2�悵��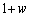 �ɂȂ镡�f�����l����̂ɕ֗��ȋZ�I���Ɍ`���ł��B�ł��A�����ŋɌ`���������o�����炢�Ȃ�A�͂��߂���Ɍ`���ŏ����Ă��������悢���낤�A�Ƃ������ƂŁAz���Ɍ`���ŁA
�ɂȂ镡�f�����l����̂ɕ֗��ȋZ�I���Ɍ`���ł��B�ł��A�����ŋɌ`���������o�����炢�Ȃ�A�͂��߂���Ɍ`���ŏ����Ă��������悢���낤�A�Ƃ������ƂŁAz���Ɍ`���ŁA
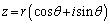 (
(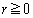 �C
�C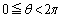 )�ƕ\�����Ƃɂ��܂��B
)�ƕ\�����Ƃɂ��܂��B
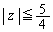 �Ƃ��������́A
�Ƃ��������́A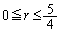 �ƂȂ�܂��B
�ƂȂ�܂��B
�����r���Œ肵�čl����ƁA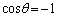 �C�܂�A
�C�܂�A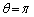 �̂Ƃ��ɍő�ɂȂ�܂��B
�̂Ƃ��ɍő�ɂȂ�܂��B
���̂Ƃ��A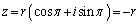 ��
��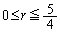 ������w��T��̓_�ɂȂ�܂��B
������w��T��̓_�ɂȂ�܂��B
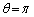 �̂Ƃ��A
�̂Ƃ��A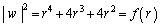 �Ƃ��āA
�Ƃ��āA
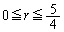 �ɂ����ẮA
�ɂ����ẮA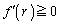 ���
���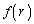 �͒P�������ŁA
�͒P�������ŁA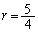 �̂Ƃ�
�̂Ƃ�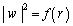 �ő�B
�ő�B
���̂Ƃ��A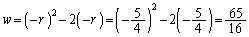
�ł����I�Ƌ��삵�����Ȃ�̂ł����A�Ƃ��đÓ����ǂ����ׂĂ݂܂��B
�@�ŁA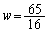 �Ƃ��Ă݂�ƁA
�Ƃ��Ă݂�ƁA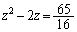
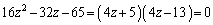 �@��
�@�� 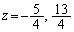
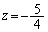 ��
��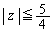 �����̂ł����A
�����̂ł����A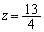 �͖������܂���B
�͖������܂���B
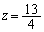 �́A�W��T�̏������F
�́A�W��T�̏������F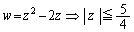 �����Ȃ��̂ł��B
�����Ȃ��̂ł��B
�܂�A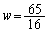 �͏W��T�̗v�f�ɂ͂Ȃ蓾���A���̖��̉Ƃ���킯�ɂ͂����܂���B
�͏W��T�̗v�f�ɂ͂Ȃ蓾���A���̖��̉Ƃ���킯�ɂ͂����܂���B
����́A�A���Aw�ɑ���z�̒l��1�ʂ�ł��邩�̂悤�Ɍ����邽�߂ł��B
�ł����A�@��2���������Ȃ̂ŁA����2�A�܂�Az�̒l��2�ʂ肠��܂��B
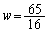 �ɑ���z��
�ɑ���z��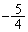 ��
��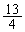 ��2����܂��B
��2����܂��B
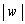 �̍ő�l�́A2���������@�̉���2�Ƃ�
�̍ő�l�́A2���������@�̉���2�Ƃ�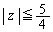 �����Ƃ����������ōl���Ȃ���Ȃ�܂���B
�����Ƃ����������ōl���Ȃ���Ȃ�܂���B
���ƌ����āA
����z�����߂�̂́A���������ł��B
�����ŁA�����P���Ȗ����l���Ă݂܂��B
�^����ꂽ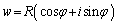 �ɑ��āA
�ɑ��āA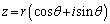 �Ƃ����A
�Ƃ����A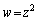 ����z�����߂Ă݂܂��B
����z�����߂Ă݂܂��B
�܂��A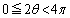 ���
���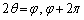 ���A
���A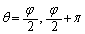
����āA
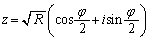 �C�܂��́A
�C�܂��́A
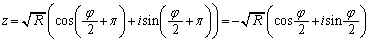 �@���(��)
�@���(��)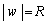 �̍ő���A
�̍ő���A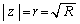 �Ɋւ�����������N�ɍl���邱�Ƃ��ł��܂��B
�Ɋւ�����������N�ɍl���邱�Ƃ��ł��܂��B
���́A�����2��́A���̒P�������ꂽ���ɋA���ł���`�����Ă��܂��B
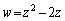 �̗��ӂ�1��������ƁA
�̗��ӂ�1��������ƁA
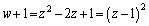 �@����B
�@����B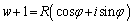 (
(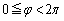 )�ɑ��āA
)�ɑ��āA
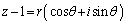 (
(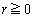 �C
�C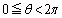 )�Ƃ����A
)�Ƃ����A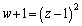 ����z�����߂Ă݂܂��B
����z�����߂Ă݂܂��B
����āA��L(��)�𗘗p���āA
���ӂ��������āA
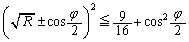 ��
�� 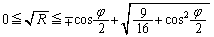 (�����܂ŁA��������) ����D
(�����܂ŁA��������) ����D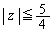 �Ƃ��������́A2���������@��2�̉��C�̑o���ɂ��Đ�������K�v������܂��B�D�̏����������́{�C�|�̑o���ɂ��Đ�������K�v������܂��B
�Ƃ��������́A2���������@��2�̉��C�̑o���ɂ��Đ�������K�v������܂��B�D�̏����������́{�C�|�̑o���ɂ��Đ�������K�v������܂��B
�܂�A�����߂�ꂽφ�����āA
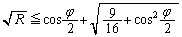 ����
���� 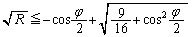
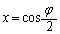 (
(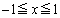 )�Ƃ���
)�Ƃ���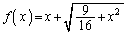 �Ƃ����ƁA
�Ƃ����ƁA
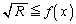 ����
���� 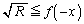 ����E
����E
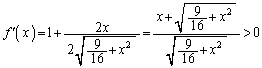 ���A
���A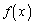 �͒P�������B�@(�������̔����@�A���̑������Q��)
�͒P�������B�@(�������̔����@�A���̑������Q��)
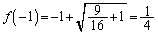 �C
�C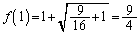 ���A
���A
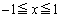 �ɂ����āA
�ɂ����āA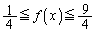
�܂��A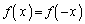 �Ƃ���ƁA
�Ƃ���ƁA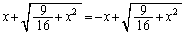 �@��
�@�� 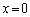
�]���āA
���͈̔͂�x�ɑ���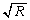 ���ő�ɂȂ�̂�
���ő�ɂȂ�̂�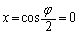 �̂Ƃ��ŁA
�̂Ƃ��ŁA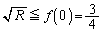
���͈̔͂�x�ɑ���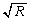 ���ő�ɂȂ�̂�
���ő�ɂȂ�̂�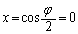 �̂Ƃ��ŁA
�̂Ƃ��ŁA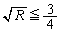
����A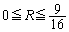 �̂Ƃ��A
�̂Ƃ��A
�E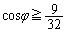 �ł���A
�ł���A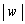 ��
��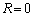 �ɂ����čő�ŁA�ő�l��1
�ɂ����čő�ŁA�ő�l��1 �E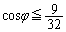 �ł���A
�ł���A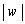 ��R�ő�̂Ƃ��ɍő�ƂȂ�܂��B�܂��AR�ő�Ƃ��������̂��ƂŁA
��R�ő�̂Ƃ��ɍő�ƂȂ�܂��B�܂��AR�ő�Ƃ��������̂��ƂŁA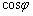 ���ŏ��̂Ƃ��ɁA
���ŏ��̂Ƃ��ɁA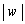 �͍ő�ł��B
�͍ő�ł��B ��L�̂悤�ɁAR���ő�l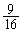 ���Ƃ�Ƃ��ɁA
���Ƃ�Ƃ��ɁA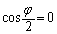 �ł����āA
�ł����āA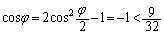 �Ȃ̂ŁAR�ő��
�Ȃ̂ŁAR�ő��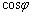 �ŏ��͓����ɋN����A�������A
�ŏ��͓����ɋN����A�������A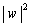 �̍ő�l�́A
�̍ő�l�́A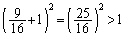
�ȏ���A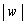 ���ő�ɂȂ�̂́A
���ő�ɂȂ�̂́A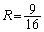 �C
�C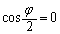 (
(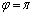 )�̂Ƃ��ŁA���̂Ƃ��A
)�̂Ƃ��ŁA���̂Ƃ��A
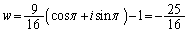 ......[��]
......[��]
�ꉞ�A�m�F�����Ă����ƁA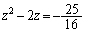 �Ƃ��āA
�Ƃ��āA
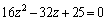 �������ƁA
�������ƁA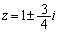 �C���̂Ƃ��A
�C���̂Ƃ��A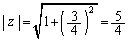 �ƂȂ�A2���Ƃ��A
�ƂȂ�A2���Ƃ��A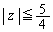 �����Ă��܂��B
�����Ă��܂��B
�ʉ��@��L�̂悤�ɑf���ɋɌ`���ł���Ă��܂��ƁA(��)����C�C�D�Ɨ��邠����ŃS�^���܂��B�����ŁA2�悵��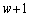 �ƂȂ镡�f�������߂Ă��܂킸�ɁA�P�ɁAα�ƒu�����Ƃɂ��܂��B����ƁA�B�F
�ƂȂ镡�f�������߂Ă��܂킸�ɁA�P�ɁAα�ƒu�����Ƃɂ��܂��B����ƁA�B�F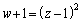 ����z�́A
����z�́A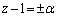 ���A
���A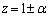 �C�܂��A
�C�܂��A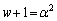 ���A
���A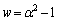
�����F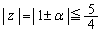 �́A�����́}�̂�����ɑ��Ă����藧�K�v������̂ŁA
�́A�����́}�̂�����ɑ��Ă����藧�K�v������̂ŁA
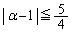 ����
���� 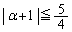
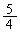 �̉~��������ł����āA���A
�̉~��������ł����āA���A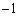 �𒆐S�Ƃ��锼�a
�𒆐S�Ƃ��锼�a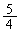 �̉~��������̕��f���ƂȂ�܂��B���̂Ƃ��A
�̉~��������̕��f���ƂȂ�܂��B���̂Ƃ��A
�ƂȂ�܂����A��������������̂́A
�̂Ƃ��ŁA2�~�̌�_�́A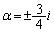 ���Aα�����̌�_�ɗ���Ƃ���w�ő�ł��B
���Aα�����̌�_�ɗ���Ƃ���w�ő�ł��B
�]���āA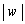 �̍ő�l��^����w�́A
�̍ő�l��^����w�́A
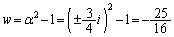 ......[��]
......[��]
�y�L���z��������L���ł��B�����̊F���܂̂��x�������������肽���A��낵�����肢�������܂��B
�y�L���z�L���͂����܂łł��B
�@�@���嗝�n���wTOP�@�@���wTOP�@�@TOP�y�[�W�ɖ߂�
�y�L���z��������L���ł��B�����̊F���܂̂��x�������������肽���A��낵�����肢�������܂��B
�y�L���z�L���͂����܂łł��B
�e���̒��쌠��
�o���w�ɑ����܂��B©2005-2024(�L)����� ��w�y�w�m ���������t���I���n��w�l�b�g�m��w�y�w�m(���ē���������)������́A
�܂��A������܂Ń��[����
�����肭�������B 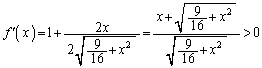 ���A
���A