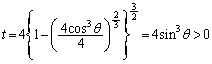���嗝�H���w'06�N[5]
���_P��x����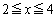 �̕����A���_Q��y����
�̕����A���_Q��y����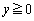 �̕�����
�̕�����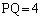 �����Ȃ��瓮���B���̂Ƃ�����PQ�������Ăł���̈��F�Ƃ���B�܂�O�͌��_�Ƃ��A
�����Ȃ��瓮���B���̂Ƃ�����PQ�������Ăł���̈��F�Ƃ���B�܂�O�͌��_�Ƃ��A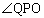 ��α�Ƃ���B
��α�Ƃ���B
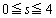 ����s���Œ肵���Ƃ��A�_
����s���Œ肵���Ƃ��A�_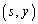 ��F�ɑ�����悤��y�̍ő�l��t�Ƃ��A����PQ���_
��F�ɑ�����悤��y�̍ő�l��t�Ƃ��A����PQ���_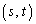 ��ʂ�Ƃ���α�̒l��θ �Ƃ���B�ȉ��̖�ɓ�����B
��ʂ�Ƃ���α�̒l��θ �Ƃ���B�ȉ��̖�ɓ�����B
(1) 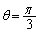 �����藧��s�͈̔͂����߂�B
�����藧��s�͈̔͂����߂�B (2) s��(1)�ŋ��߂��͈͂ɑ����Ȃ��Ƃ�s�Ct��θ �ŕ\���B
(3) F�̖ʐς����߂�B
�y�L���z��������L���ł��B�����̊F���܂̂��x�������������肽���A��낵�����肢�������܂��B
�y�L���z�L���͂����܂łł��B
���@�A�X�e���C�h�ɂȂ�̂��낤�Ƃ������Ƃ͗\�������܂����A��蕶���ς��ƌ��������ł́A(1)������v�����Ă���̂����ǂݎ��Ȃ������m��܂���B�����Ȃ�(1)�����悤�Ƃ����̂łȂ��A�O�x�߂邱�Ƃ���n�߂܂��B
����PQ�̌X��(���ł�)�̐�Βl���ł��傫���Ȃ�̂́AP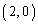 �CQ
�CQ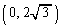 �̂Ƃ��ł��B���̂Ƃ��A
�̂Ƃ��ł��B���̂Ƃ��A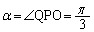 �ł��B
�ł��B
��ӂ����悤�ɐ���PQ�������Ƃ��Aα�́A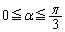 �͈̔͂��܂��B
�͈̔͂��܂��B
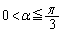 �ł���A
�ł���A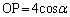 �C
�C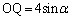 �Ȃ̂ŁA����PQ�̕������́A
�Ȃ̂ŁA����PQ�̕������́A
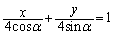 �@����@
�@����@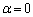 �̂Ƃ��ɂ́AP
�̂Ƃ��ɂ́AP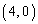 �CQ
�CQ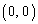 �ł����āA����PQ�̕������́A
�ł����āA����PQ�̕������́A
�܂��A���̂Ƃ��A����PQ��̓_�ŁA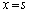 (
(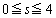 )�ɑΉ�����_��y���W�́A
)�ɑΉ�����_��y���W�́A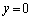 �ł��B
�ł��B
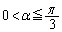 �̂Ƃ��A�B��
�̂Ƃ��A�B��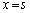 �Ƃ����ƁA
�Ƃ����ƁA
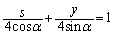 ������A����PQ��ł̓_�ŁA
������A����PQ��ł̓_�ŁA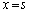 (
(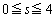 )�ɑΉ�����_��y���W�́A
)�ɑΉ�����_��y���W�́A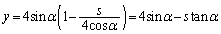 �@����A
�@����A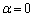 �̂Ƃ�����PQ�F
�̂Ƃ�����PQ�F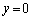 �C�܂�
�C�܂�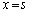 �ɑΉ�����y���W��
�ɑΉ�����y���W��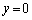 �ł����A�A�͂�����܂�ł��܂��B
�ł����A�A�͂�����܂�ł��܂��B
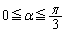 �ɂ����ćA�̍ő�l���l���܂��B
�ɂ����ćA�̍ő�l���l���܂��B
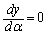 �Ƃ���ƁA
�Ƃ���ƁA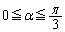 �͈̔͂ɂ����āA
�͈̔͂ɂ����āA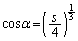 �@����B
�@����B
���̂Ƃ��A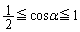 �Ȃ̂ŁA
�Ȃ̂ŁA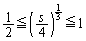 �C�܂�A
�C�܂�A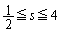 �@����C
�@����C
s��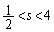 �͈̔͂ɂ���A�B����α�����݂��āA����α��
�͈̔͂ɂ���A�B����α�����݂��āA����α��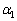 �Ƃ���ƁA
�Ƃ���ƁA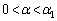 �ɂ����ẮA
�ɂ����ẮA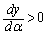 �C
�C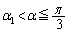 �ɂ����ẮA
�ɂ����ẮA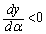 �ƂȂ�̂ŁA
�ƂȂ�̂ŁA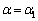 �̂Ƃ��A�܂�B�����藧�Ƃ��ɁAy�͍ő�l���Ƃ�܂�(���̑������Q��)�B�@����D
�̂Ƃ��A�܂�B�����藧�Ƃ��ɁAy�͍ő�l���Ƃ�܂�(���̑������Q��)�B�@����D
���̂Ƃ��A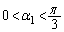 �Ȃ̂ŁA
�Ȃ̂ŁA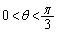 �ł����āA
�ł����āA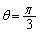 �ɂ͂Ȃ蓾�Ȃ����Ƃɒ��ӂ��Ă��������B
�ɂ͂Ȃ蓾�Ȃ����Ƃɒ��ӂ��Ă��������B
�B��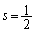 �Ƃ���ƁA
�Ƃ���ƁA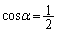 �ŁA
�ŁA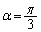 �ł��B���̂Ƃ��A
�ł��B���̂Ƃ��A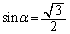 �ŁA����PQ�̕������@�́A
�ŁA����PQ�̕������@�́A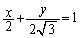 �ƂȂ�܂��B
�ƂȂ�܂��B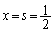 �̂Ƃ��Ay�̍ő�l�́A�����̕���������A
�̂Ƃ��Ay�̍ő�l�́A�����̕���������A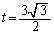 �ƂȂ�܂��B
�ƂȂ�܂��B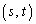 �͒�����̓_�Ȃ̂ŁA���̂Ƃ���α��θ �Ƃ���A
�͒�����̓_�Ȃ̂ŁA���̂Ƃ���α��θ �Ƃ���A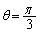 �ł��B�@����E
�ł��B�@����E
�B��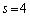 �Ƃ���ƁA
�Ƃ���ƁA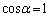 �ŁA
�ŁA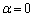 �ł����āA
�ł����āA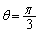 �ɂ͂Ȃ�܂���B
�ɂ͂Ȃ�܂���B
���������ƁA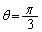 �ɂȂ�̂́A
�ɂȂ�̂́A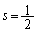 �����ŁAs�͈̔͂Ȃ�ďo�Ă��Ȃ��A�ƁA�v�������m��܂��A�����ŁA�u���_P��x����
�����ŁAs�͈̔͂Ȃ�ďo�Ă��Ȃ��A�ƁA�v�������m��܂��A�����ŁA�u���_P��x����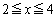 �̕����v��(
�̕����v��(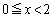 �̕����ɂ͍s���Ȃ�)�A�Ƃ�����蕶�̏����Ƀs���Ɨ��Ȃ��Ƃ����܂���B
�̕����ɂ͍s���Ȃ�)�A�Ƃ�����蕶�̏����Ƀs���Ɨ��Ȃ��Ƃ����܂���B
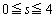 �Ȃ̂ŁA
�Ȃ̂ŁA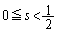 �̏ꍇ���c���Ă��܂��B
�̏ꍇ���c���Ă��܂��B
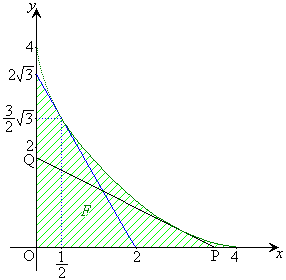
(1) ��L�ŁA�C����������Ȃ��Ƃ��A�܂�A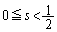 �̂Ƃ��A�B����α�͑��݂����A
�̂Ƃ��A�B����α�͑��݂����A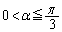 �ɂ����āA
�ɂ����āA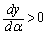 ���y��α�̑������ŁAy��
���y��α�̑������ŁAy��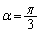 �̂Ƃ��ɍő�lt���Ƃ�܂��B
�̂Ƃ��ɍő�lt���Ƃ�܂��B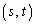 �͒���PQ�F
�͒���PQ�F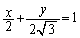 ��̓_�Ȃ̂ŁA���̂Ƃ���α��θ �Ƃ���ƁA
��̓_�Ȃ̂ŁA���̂Ƃ���α��θ �Ƃ���ƁA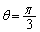 �ƂȂ�܂��B
�ƂȂ�܂��B ��L�̇E���܂߂āA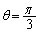 �����藧��s�͈̔͂́A
�����藧��s�͈̔͂́A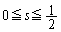 ......[��]���D�����Ȃ��Ƃ���点��U�������Ă��܂����A�v����ɁA���̖��ł́A�E�}�̂悤�ɁA�̈�F��
......[��]���D�����Ȃ��Ƃ���点��U�������Ă��܂����A�v����ɁA���̖��ł́A�E�}�̂悤�ɁA�̈�F��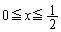 �̕����̏㑤�̋��E��(�ex�ɑ���y���ő�ƂȂ�_�̏W��)���A�����F
�̕����̏㑤�̋��E��(�ex�ɑ���y���ő�ƂȂ�_�̏W��)���A�����F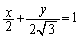 �ɂȂ�Ƃ������Ƃ������Ă��܂��B
�ɂȂ�Ƃ������Ƃ������Ă��܂��B
(2) 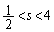 �̂Ƃ��A��L�̇C���Ay�̍ő�lt�́A�A�C�B�C
�̂Ƃ��A��L�̇C���Ay�̍ő�lt�́A�A�C�B�C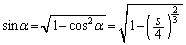 ���A
���A 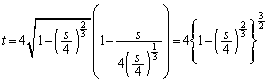 �@����F
�@����Fy���ő�lt���Ƃ�Ƃ��A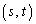 �͒���PQ��̓_�ŁA���̂Ƃ��A
�͒���PQ��̓_�ŁA���̂Ƃ��A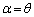 �Ȃ̂ŁA�B���A
�Ȃ̂ŁA�B���A 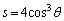 (
(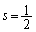 �̂Ƃ��ɂ����藧���܂�)
�̂Ƃ��ɂ����藧���܂�)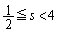 �̂Ƃ��A�F���A
�̂Ƃ��A�F���A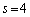 �̂Ƃ��A���炩�ɁA�̈�F�ɂ́A
�̂Ƃ��A���炩�ɁA�̈�F�ɂ́A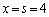 �ƂȂ�_��
�ƂȂ�_��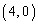 �����Ȃ��A
�����Ȃ��A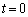 �ł����A������܂߂āA
�ł����A������܂߂āA
(3) �̈�F�̂����A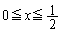 �̕����́A����
�̕����́A����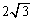 �C���
�C���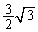 �C����
�C����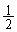 �̑�`�ŁA���̖ʐς́A
�̑�`�ŁA���̖ʐς́A 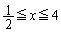 �̕����́A�Ȑ��F
�̕����́A�Ȑ��F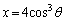 �C
�C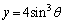 ��x���̊Ԃɋ��܂ꂽ�����ŁA�����ʐ��́A
��x���̊Ԃɋ��܂ꂽ�����ŁA�����ʐ��́A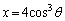 �ƒu������ƁA
�ƒu������ƁA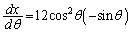 ���A
���A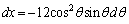 �Cx�F
�Cx�F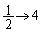 �̂Ƃ��Aθ �F
�̂Ƃ��Aθ �F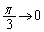 (�u���ϕ����Q��)
(�u���ϕ����Q��)���߂�ʐς́A
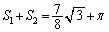 ......[��]
......[��]
�y�L���z��������L���ł��B�����̊F���܂̂��x�������������肽���A��낵�����肢�������܂��B
�y�L���z�L���͂����܂łł��B
�@�@���嗝�H���wTOP�@�@���wTOP�@�@TOP�y�[�W�ɖ߂�
�y�L���z��������L���ł��B�����̊F���܂̂��x�������������肽���A��낵�����肢�������܂��B
�y�L���z�L���͂����܂łł��B
�e���̒��쌠��
�o���w�ɑ����܂��B©2005-2024(�L)����� ��w�y�w�m ���������t���I���n��w�l�b�g�m��w�y�w�m(���ē���������)������́A
�܂��A������܂Ń��[����
�����肭�������B 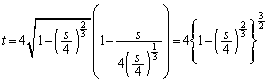 �@����F
�@����F